Математическая модель процесса радиационно–конвективной сушки фруктовых и овощных чипсов при импульсном энергоподводе

Общая задача моделирования процессов тепломассопереноса при радиационно - конвективной сушке ломтиков фруктов и овощей состоит из двух составляющих.

Первая математическая модель (внешняя задача) описывает период постоянной скорости сушки, который связан с уносом свободной влаги с поверхности фруктов и овощей до достижения ею равновесного состояния, за счет конвективного обдува теплоносителем. Температура теплоносителя равна температуре окружающей среды.

Отработанный теплоноситель

Рисунок 1 - Расчетная схема радиационноконвективной сушки фруктовых и овощных чипсов

Вторая математическая модель описывает период убывающей скорости сушки, когда фронт испарения влаги проникает внутрь продукта.

Запишем математическую модель процесса сушки для единичной пластины исследуемого продукта. Примем пластину постоянной толщины, но предположительно близкой к круглой форме. Начало системы пространственных координат поместим в произвольную точку, близкую к геометрическому центру пластины. Будем считать, что пластина ориентирована перпендикулярно потоку инфракрасных лучей.

Ось координаты x направим параллельно потоку инфракрасных лучей и перпендикулярно поверхности пластины. Координатную плоскость ( y , z ) расположим перпендикулярно оси x и параллельно поверхности ломтика (как мы увидим ниже, координаты y и z не участвуют в уравнениях, описывающих процесс сушки). Время обозначим τ , начальный момент сушки принимаем за τ =0.

Состояние продукта во время сушки описывается двумя основными переменными: температурой T и влагосодержанием U .

Изменение температуры T и влагосо-держания U в процессе сушки описывается системой дифференциальных уравнений тепло- и массопереноса, приведенной в [5]:

'д и дт

„ ди b V и + b5V T + s--, дт дT srUr 9U — = a V T +---.

_дт c дт где

_V= g 2 + д ² ₊ a ² д x ² д y ² д z ²

оператор Лапласа,

a - температуропроводность продукта, м2/с, b - коэффициент массопереноса (диффузии), м2/с, 5 - термоградиентный коэффициент, s - коэффициент фазового превраще ния, r - удельная теплота испарения воды, кДж/кг; c - удельная массовая теплоемкость вещества, кДж/(кг-К).

Поскольку в процессе сушки структура продукта претерпевает изменения, его теплофизические, оптические и другие параметры (плотность, температуропроводность, теплоемкость и т. д.) меняются. Для достижения точного решения уравнений необходимо учитывать изменения этих параметров в процессе радиационно-конвективной сушки.

Зависимость коэффициента температуропроводности a , коэффициента теплопроводности X и массовой удельной теплоемкости c от температуры и влажности вещества описана в [8]. Согласно обобщению экспериментальных данных, каждый из этих коэффициентов при фиксированном влагосодержании линейно зависит от температуры:

a = a 0 ( ^U ) ⁺ k a T = a 0 ( ^U ) ⁺ k a T

X = Xo (и) + kxT = Xo (U) + kxT c = Co (U) + kcT = co (U) + kcT где коэффициенты a0, ka, Xo, kX, c0, kc принимают определенные значения для каждого конкретного продукта.

Коэффициенты поглощения, отражения и пропускания лучистого потока будем, несколько упрощая, считать постоянными. Коэффициент поглощения будем обозначать А . В связи с доминирующим перемещением влаги вдоль оси х, высоким градиентом влагосодер-жания, незначительными внутренним влагопе-реносом по координатам у , zu последующим испарением через кожуру, температура и вла-госодержание не зависят от координат y , z

следовательно, уравнения (1) принимают вид:
	д U , д 2 U ,,82T д U = b + b 5 + s , дт     д x 2       д x 2     дт
	д T   д 2 T s r д U = a +        . _дт     д x 2 c дт	(2)

В уравнение теплопереноса необходимо добавить слагаемое, отвечающее за инфракрасный нагрев. Пусть мощность падающего на вещество лучистого потока равна q(т). То- гда мощность поглощенного потока в точке вещества с координатой x равна:

q (т) = Aq (т) exp (k (R - x)), где k - коэффициент инстинкции (коэффициент ослабления луча) [5].

Сложение двух лучистых потоков от ламп, находящихся по разные стороны от пластины, даст прогрев, не зависящий от координаты x : q ( т ) = Aq ( т ) .

Таким образом, уравнение теплоперено- са принимает вид:

д T    д ² T s r д U

= a ++     Aq . ( 3 )

дт    д x ²    c дт c p

При точном решении уравнений необходимо учитывать зависимость коэффициентов от времени. С учетом этой зависимости система уравнений может быть записана так:

'д U , , ., ,/^; U, , 7 7 ^{( x т} ) = ^{b Т} ’a?^{( xт ) +}

^{+ b ( т} ) ^{5 ( т )}& T ⁽ x ^{- г ) + s ( x , т} ) Т 7 ^{( x , т} ) ’

‘ дT, , , ч д2T, , s(x,т)r дU , , —( x ,Т ) = a (Т )-т( x ,т) +--——( X ,Т ) + дт             дx           c(т) дт pw + psU (x,Т)

[ c ( т ) P s P w ( U ( x, т ) + 1 ) q^(Т ) , Уравнение (4) можно переписать в эквивалентном виде (учитывая, что s ( x, т ) ^ 1 ра^, венство означало бы, что влага не испаряется с поверхности пластины):

д U/ А ---( xТ ) = дт V 7

^{b т} ) ^д:U ( x , _г ) + 1 - s ( x, т ) д x²

b ( т ) 5 ( т ) д² T,    _х                      х

+ ^v Л _х т( x, Т ) .                 ( 4' )

1 - s ( x, т ) д x¹¹

Опишем теперь начальные и граничные условия. В момент начала сушки ( т = 0) принимаем температуру и влагосодержание за постоянные величины:

T ( x ,0 ) = T _o, U ( x ,0 ) = U ₀        ( 6 )

Ввиду малой толщины ломтика, мы пренебрегаем процессами, происходящими на краю диска, поэтому граничные условия мы будем записывать лишь для x = ± R , то есть фактически рассматриваем задачу для бесконечной пластины.

Пренебрегая бародиффузией и термо-влагопроводностью (поскольку их вклад становится заметным лишь при температурах порядка 100 °С [5]), запишем граничное условие для уравнения массопереноса в виде условия третьего рода на поток влаги, испаряющейся через поверхность пластины:

—A ( R,т ) d U ( R^,т ) =

= ^{в (} Rт ) P+UUUИ ⁽ U ⁽ R' ^{) -} U -p ) ■⁽7 ) где A m - коэффициент массопроводности,

Прежде всего, воспользуемся малой толщиной пластины (в рассматриваемом опыте она равна 1,5 - 10 — 3 м, то есть R = 7,5 - 10 — 4 м). Это позволяет разложить неизвестные функции U ( x , т )

и T ( x , т ) в ряды по переменной x :

U ( x , т ) = и ₀ ( т ) + U 1 ( т ) x + и 2 ( т ) x ² +— , T ( x , т ) = t ₀ ( т ) + t 1 ( т ) x + t 2 ( т ) x ² +— .

в - коэффициент массоотдачи, U cp содержание окружающей среды.

Из соображений симметрии «внутреннее» граничное условие:

( °, т ) = 0

о x

– влаго-

получим

Аналогично запишем граничные условия для уравнения теплопереноса:

-A T ( R , т ) + “ ( ^т ( R ^ ) — ^Tcp ) =

= в ( R т ) r ^)^Up^R'',. ) + ^{1 8} ( R ■ ' ) ( U ( R ■ ' ) - U" ) ^, ( 9 )

ww ⁺ Ps^u Vт )

Β силу симметрии задачи по x (пластина однородна и симметрична, воздействие постоянно по x , то есть тоже симметрично) функции U ( x , т ) и T ( x , т ) четны по x , это означает, что ряды будут содержать только слагаемые с четными степенями x . Подставим эти выражения в систему уравнений и начальнокраевых условий, затем отбросим слагаемые степени выше 2 как пренебрежимо малые, то есть функции U и R будем приближенно ис-

кать в виде:

U ( x , т ) ® U ₂ ( x , т ) = и ₀ ( т ) + и ₂ ( т ) x ², T ( x , т ) ® T ₂ ( x , т ) = t ₀ ( т ) + t ₂ ( т ) x ²

8Т_ 5x здесь A - коэффициент теплопроводности вещества, а - коэффициент теплоотдачи.

Конкретизируем теперь вид уравнений на разных этапах сушки.

На первом этапе инфракрасные лампы дают постоянный лучистый поток, так что в уравнении (5) q ( т ) = const. Подставляя это

( 0 т ) = о                ( 10 )

Уравнение массопереноса, его начальное и краевое условия (мы отправляемся от уравнения в виде (3.7’), точкой обозначается производная по времени):

и₀ ( т ) + и₂ ( т ) x ²

2 b ( т )

1 - е ( x ,т )

( и ₂ ( т ) + 6 и 4 ( т ) x ² )

+

^{+ 2 Ь}-^т ^ ^т ) ( t 2 ^{( т ) + 6t} 4 ^{( т} ) x ² ) ,                ^{( 13 )}

1 - 8 ( x , т ) '

и ₀ ( 0 ) + и ₂ ( 0 ) x ² = U ₀          ( 14 )

выражение в систему с учетом граничных и начальных условий, задачу можно решить численно.

Однако экспериментальные измерения не отражают зависимость этих величин от x . В случае с влагосодержанием эксперимент дает возможность судить о его среднем (имеется в виду пространственное усреднение в каждый момент времени) значении:

m_, (т) U (т ) = -Awa .

m _s

Что же касается температуры, то она измеряется на поверхности продукта, поэтому здесь мы имеем дело со значением T ( ± R , т ) .

Систему уравнений (4) – (5) решить затруднительно. Поэтому для анализа поставленной задачи воспользуемся приближениями.

2A _m ( R,т ) и 2 ( т ) R = в ( R,т )

PsP^ ( ^и 0 ( ^т ) ^{+ и} 2 ( ^т ) ^{R 2 +} 1 ) P w ⁺ P s ( ^и 0 ( ^т ) ^{+ и} 2 ( ^т ) ^R 2 )

• ( ^и 0 ( ^т ) ^{+ и} 2 ( ^т ) ^{R 2 - U} _т )                             ( 15 )

Уравнение теплопереноса (16) содержит слагаемое                   — Aq ( т ) , которое

c(т)PsPw (U(x,т) +1)    V ’ необходимо разложить по степеням x :

Pw + PsU (x, т)    Aq (т) = c (т ) PsPw ( U ( x ,т ) + 1)

Aq ( P w ⁺ P s ( ^и 0 ( ^т ) ^{+ и} 2 ( ^т ) x ² ) )

P s P w c ( ^т ) ( ^и 0 ( ^т ) ^{+ и} 2 ( ^т ) x 2 ⁺ 1 )

Aq      ^P w ^{+ P}s^U 0 ^{( т} ) , P s - P w „ 2_tA_y2

_PsP c C ( г ) [ 1 + и 0 ( г )      ( 1 + и 0 ( т ) ) ² 2 ⁽ )

Таким образом, уравнение теплоперено-са с начальным (для первого периода сушки) и краевым условиями приобретает вид:

t ₀ ( т ) + t₂ ( т ) x ² = 2 а ( т ) ( t ₂ ( т ) + 6 t ₄ ( т ) x ² ) +

^ ⁽ x,^т ) ri. / \ . / \ 2\ Aq ■,\и 0 ( т ) ⁺ и 2 ( т ) x ) ^{+ +}----^х c ( ^т ) ^V ’    P s P w c ( ^т )

P w ⁺ P s u 0 ^{( т} ) + P s - P w ^{1 + U} 0 ^{( т} )      ( 1 + и ₀ ( т )

и ₂ ( т ) x ² , ( 16 )

- ^{2 1 t} 2 ( ^т ) R + « ( t 0 ( ^т ) ⁺ t 2 ( ^т ) R ^{2 -} T cp ) =

в ( R , т ) Г

P s P w ( ^U 0 ( ^т ) ^{+ U} 2 ( ^т ) R ^{2 +} 1 ) P w ⁺ P s ( ^U 0 ( ^т ) ^{+ U} 2 ( ^т ) R ² )

. £ ( R , t ) ( и 0 ( т ) + и 2 ( т ) R ² - U cp ) ,         (17)

1 0 ( 0 ) + t 2 ( 0 ) x ² = T

Отметим, что внутренние граничные условия (16) и (17) уже учтены, они являются следствием четности функций U и T по x .

Согласно [1, 6], на первом этапе сушки изменение величины коэффициента фазового превращения ^ ( x , т ) весьма незначительно, и можно положить его равным 0. Перепишем соотношения, описывающие теплоперенос, с учетом этого обстоятельства:

t ₀ ( т ) + t ₂ ( т ) x ² = 2 а ( т ) ( t ₂ ( т ) + 6 t ₄ ( т ) x ² ) +

, Aq      ^P w ^{+ P} s^U 0^{( т} ) , P s ^- P w „ 7X2

+                     + и т x

P s P w c ( ^т ) ( ^{1 + и} 0 ( ^т )      ( 1 + и ₀ ( т ) )

^{- 2 1 t} 2 ( ^т ) R + а ( t 0 ( ^т ) + t 2 ( ^т ) R ^{2 -} Т_С р ) = ⁰

1 0 ( 0 ) + t 2 ( 0 ) x ² = T

Выше приведены выражения для коэффициентов температуропроводности и теплоемкости:

а = а _п + k T + l -----,

0 а     а 1 + U c = cn + k T +1 -----.

^{0 c c} 1 + U

Как показали эксперименты, за время этапа постоянной скорости сушки коэффициент температуропроводности а меняется незначительно, тем более что его увеличение за счет повышения температуры отчасти компенсируется уменьшением за счет снижения вла-госодержания. Поэтому для первого этапа мы примем значение этого коэффициента постоянным и равным а к а = 4,9Л0 ^{- 8} м² /с [8].

Аналогично, теплоемкость примем равной c К c = 3600 Дж/(кг ■ К).

После упрощения правой части и отбрасывания слагаемых порядка выше 2 по х уравнение приобретает вид:

.               .             2

1 0 ( т ) + 1 2 ( т ) x = 2 a 1 1 2 ( т ) +

Aq ⁽ P w + P s^uo ^{( т} )) + ₂ ^Aa1 q ^P s ^P w^c1 ^{(1 + U}o ^{( т} )) ^P s ^P w^c1

■

• ■ 6 ^P w ^{+ P} s^Uo ^{( т} ) 1 ₄( т ) +   ^P s - ^P w

_v ^{1 + и}о ^{( т} )            (1 + и_о ( т ))²

2 и 2 ( т ) 1 2 ( т ) x

Приравняем коэффициенты при одинаковых степенях x :

t o ^{( т} ) = ^{2 а} 1 t 2 ^{( т} ) ⁺

«

Aq ⁽ P w + P s^uo ^{( т} )) P s P w^c 1 ^{(1 +} u o ^{( т} ))

. э Aa1 q 1й Pw + Psuo(тТ t 2(т ) = 2------ 6 —w-----—t 4(т ) +

P s P w^c1 (      ^{1 +} u o ^{( т} )

P s ^- P w

^{(1 +} U o ^{( т ))2}

^и 2 ^{( т} ) t 2 ^{( т} )

Изменения коэффициента теплопроводности 1 (который участвует в граничном условии для уравнения теплопереноса) на первом этапе сушки не превосходят 2-3 %, мы примем этот коэффициент равным приблизительно 1 к 1 1 = 0,2 Вт /(м ■ К).

Уравнение массопереноса с учетом допущения s ( х , т ) = 0 принимает вид:

.                                             .

U o ( т ) + и 2 ( т ) x ² = 2 b ( т )( и ₂ ( т ) + 6 и ₄ ( т ) x ² ) +

+ 2 b ( т ) § ( т )( 1 ₂( т ) + 6 1 ₄( т ) x ² )                    .

Приравнивание коэффициентов при одинаковых степенях х дает систему:

U o ( т ) = 2 b ( т ) и ₂ ( т ) + 2 b ( т ) 8(т ) 1₂( т ), .

и 2 ( т ) = 12 b ( т ) и ₄( т ) + 12 b ( т ) 8 ( т ) 1 ₄( т ).

Значения коэффициента массопереноса (диффузии) b и термоградиентного коэффициента 5 будем считать постоянными.

Выпишем значения констант, участвующих в системе уравнений тепло- и массопереноса. Мощность теплового потока примем равной q = 1,2 ■Ю3 Вт/м2. Коэффициент по глощения для персика в соответствии с экспериментальными данными примем равным А к 0,57. Значение плотности влаги примем з ,    3

равным плотности воды: P w = 10 кг/м . Зная плотность продукта при исходной влажности 86 % и при влажности 7,74 %, найдем плотность абсолютно сухого вещества: P _s к 1,353-10³ кг/м³. Коэффициент диффузии b примем равным b = 2,71 ■Ю ^{- 10} м² /с.

Как показывают эксперименты [52], термоградиентный коэффициент 5 весьма мал при высоких значениях влагосодержания, поэтому на первом этапе сушки мы им пренебрежем.

Поскольку материал подвергается постоянному обдуванию воздухом, который уносит влагу, значения Т ср и U _с р постоянны,

Т ср = 22,5

C.

На втором этапе сушки мощность лучистого потока такая, чтобы обеспечивать постоянную температуру продукта. Таким образом, левая часть уравнения (1) оказывается тождественно равной 0. Подставляя в уравнения (1) и (2) в граничные условия известные значения констант, задачу можно решить численно (начально условие для уравнения второго пе- риода сушки получается из решения уравнения для первого периода).

На втором этапе сушки температура по- стоянна и задача сводится к построению функции влагосодержания. Поскольку темпе ратура, в силу нагрева, выравнивается практически по всей толще продукта, слагаемое, со-д2 Т держащее —2", из уравнения массопереноса дx 2

пропадает, и это уравнение приобретает вид:

д U_{( W}x⁸¹ U, х⁹ U —⁽ x , г ) = b ( т ) . ⁽ x^{, т} ) + £ ⁽ x , т )— дт д x дт

( X , т ) ( 20 )

или дU    .

—^{( x , т} ) = дт

^е4 ( X , т )

1 - £ (X, т ) д X ²

Коэффициент b( т ), как и для первого этапа, будем считать постоянным и равным b = 2,71 - 10 ^{- 1} ° м ² /с ; величину е (x , т ) положим равной 0,3. Коэффициент —b- )— = 3,87 - 10 ^{- 10} м ²/с обозначим B . 1 - е ( x , т )

Начальное условие приобретает вид: U (x, т0) = C0 + C2 x2          (22), где константы С0, С2 могут быть найде ны из среднего значения U (т0), определенного экспериментально, и из граничного условия.

Принимая U (т0) = 0,5 (примерное значение влагосодержания в момент, когда температура продукта стабилизируется), получаем соотно- шение CR + -C^R3 = 0,5. 0      3 2         ,

Граничное условие в данном имеет вид:

,    . SU ,

A m ( R , т ) — ( R , т ) = в R , т ) ■

дx

■ ^{P s P w ( U (} R ^{, т} ) ⁺ 1) ( U ( R , т ) - U_cр ) P w + P s U ( R , т )

или

-U (R ,т) = в*Г. ■ дx      2 Am (R,т)

■ ^{P s P w ( U ( R , т} ) ⁺ 1) ( U ( R , т ) - U_cД P w + P s U ( R , т )

случае

Как и прежде, полагаем U_cp = 0 . Поскольку значения p s и p w отличаются незначительно, используем приближенное равенство:

P s P w ( U ( R, т ) + 1) = P w ( U ( R, т ) + 1) ^ _P . ^P w ^{+ P} s ^{U ( R , т} ) ( U ( R , т ) + P w ) w

P s

Для коэффициентов массопроводности

Am (R,т) и массоотдачи в(R,т) возьмем по стоянные значения:

A m ( R , т ) = 1,6 ■Ю ^{- 3} кг/(м ■ с), в ( R , т ) = 2 ■Ю ^{- 5} м/с [4].

При сделанных допущениях граничное условие приобретает вид:

dU

^U (R ,т) = KU (R ,т), дx где K = ePw ~ 0,12 м-1.

Am

Запишем задачу массопереноса при сделанных допущениях:

^U- ^{( x , т} ) = в ^ U ^{( x} , t х ^{дт          д x}

• ( x ,т 0 ) = C 0 + C 2 x ²,             ( 26 )

dU

--( R , т ) = KU ( R , т ). д x

Система уравнений (26) представляет собой начально - краевую задачу третьего рода для уравнения теплопроводности, решение которой хорошо известно [2, 3, 9]. Воспользуемся частным случаем этого решения справедливым при Bi ~1 или Bi >>  1.

U ( х , т ) = D 1 exp( - В ц 2 т )cos ц х + D 0 , где D 1 , ц , D ₀ - константы, которые могут быть определены из начального и граничного условия.

Была выбрана именно эта форма решения, поскольку функция cos ц х близка (с точностью до слагаемых четвертого порядка) к квадратичной функции, а в качестве начального условия задан параболический профиль влажности.

Для проверки адекватности математической модели сопоставим теперь функции температуры и влагосодержания, полученные из решения системы уравнений, с измеренными экспериментальными данными для одного опыта. Измеренными величинами в этом опыте были влагосодержание и температура продукта.

На первом этапе сушки численное решение с помощью математического пакета Maple 14 системы уравнений (19) тепло- и массопереноса дает близкую к линейной зависимость от времени функций температуры и влагосодержания.

Для второго этапа, подставляя значения констант в систему (26), получим функцию, среднее значение которой U( т ) при умножении на соответствующую константу позволяет построить кривую сушки , приведенную на рисунке 2 совместно с линейной аппроксимацией для экспериментально определенных значений. Результаты вычислений в сопоставлении с результатами опытов показаны на рисунке 2.

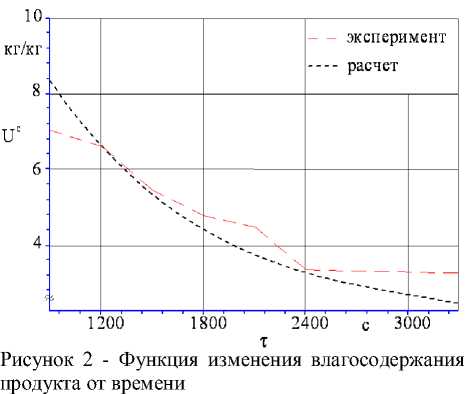
Полученные данные приведены в таблице 1.

Таблица 1

Вычисленные по модели и экспериментальные значения влагосодержания продукта

Вре мя, мин	Uc (мо-дельн.), кг/кг	Uc (экс-перим.), кг/кг	Абсолютная разница, кг/кг	Относит. разница, %
20	6,34	6,34	0	0
25	5,36	5,67	-0,31	5,46
30	4,08	5,01	-0,93	18,56
35	3,19	4,98	-1,79	35,94
40	3,09	3,35	-0,26	7,76
45	2,37	3,34	-0,97	29,04
50	1,50	3,06	-1,56	50,98
55	1,00	2,99	-1,99	66,55

Можно сделать вывод, что погрешность накапливается к концу процесса радиационноконвективной сушки. Очевидно, это связано с тем, что модель учитывает не все факторы, влияющие на процесс, а также с упрощениями, допущенными в самой модели. В первой половине второго этапа сушки математическая модель обеспечивает удовлетворительную точность.

Расчет средней относительной ошибки на протяжении всего процесса не превышает 20 % и показывает соответствие расчетных данных с экспериментальным значениям.