Математические модели сушки макаронных изделий
Автор: Джамашева Р.А., Дараева Г.Д.
Журнал: Вестник Алматинского технологического университета @vestnik-atu
Рубрика: Техника и технологии
Статья в выпуске: 1 (102), 2014 года.
Бесплатный доступ
В статье согласно структурной схеме определены выражения передаточных функций для дальнейшего выбора способа регулирования режимов сушки и построения системы автоматического управления. Актуальность работы заключается в разработке математической модели сушильных установок по каналам, связывающим изменения параметров материала и сушильного агента (воздуха) с изменением притока теплоты.
Сушка макаронных изделий, сушилка, автоматизация, математические модели, передаточная функция
Короткий адрес: https://sciup.org/140204707
IDR: 140204707 | УДК: 664.6/7
Текст научной статьи Математические модели сушки макаронных изделий
Для получения динамических характеристик конвективных сушилок можно использовать структурные схемы связи между
при этом Ta соответствует знаку «+», а Tb -
отдельными параметрами уравнения звеньев этих исходя из уравнения
сушилок, причем схем определяют теплового и
материального балансов и ряда статических соотношений [1]
Объект и методы исследований
В качестве объекта исследования рассмотрен процесс сушки макаронных изделий в конвективных сушилках В качестве методов исследования применены методы математического моделирования, дифференциального и интегрального исчисления
Результаты и их обсуждения:
Исходя из структурной схемы, представленной на рисунке 1, и уравнений звеньев, были получены следующие выражения передаточных функций конвективных сушилок:
1 По каналу «изменение подачи теплоты – изменение температуры воздуха»:
знаку «-» перед корнем;
koci = k 1 h1 Gb
2 По каналу «изменение подачи теплоты – изменение относительной влажности воздуха»:
W ( p ) = A ^ ( p ) = " A Q ( p )
лоты
^
T
c = Tc
2 ^ 0 k 1 (1 + T c* p ) (2)
( t г ) o (1 + Tap )(1 + T b p),
^
3. По каналу
–
риала»:
изменение
w ( p ) =
^
( t ^^0 hkG
2 d 0 1 7
«изменение подачи теп- влагосодержания мате-
h 1 k 1
(1 + T a p )(1 + T,p )’
На рисунке 1 приведена структурная схема, исходя из которой можно определить статические и динамические характеристики конвективной сушилки по каналам, связы-
1 + T Р
W( p ) = k 1
(1 + TQP )(1 + T b p )’
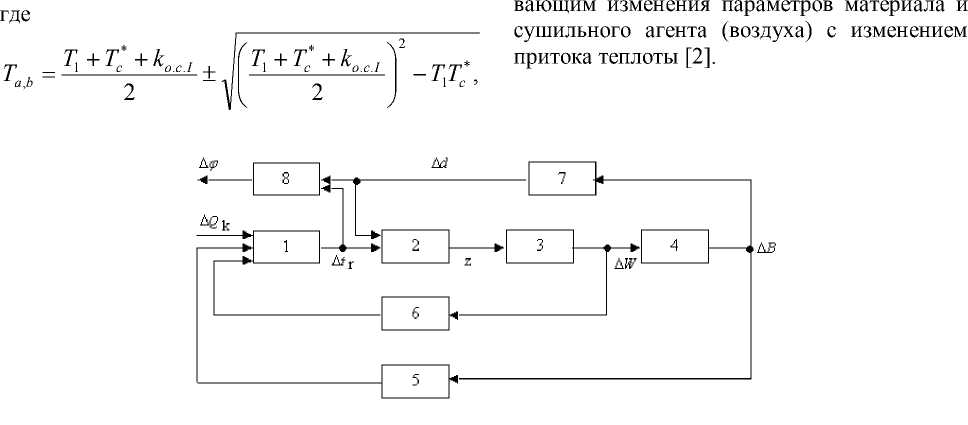
Рисунок 1 - Структурная схема системы управления процессом сушки: 1-8 звенья.
Звено 1 характеризует инерционность процесса теплообмена в сушилке Его передаточная функция находится из уравнения теплового баланса сушилки
Q = Q1 + Q2 + Q3 + Q4 + Q5, (4)
где: Q - тепловой поток, Дж;
Q 1 - расход тепла на испарение влаги, Дж;
Q 2 - расход тепла на нагревание воздуха, Дж;
Q 3 - расход тепла на нагревание материала, Дж;
Q 4 - расход тепла на нагревание транспортных приспособлений, Дж;
Q 5 - потери тепла в окружающую среду, Дж.
Поскольку влияние Q 2 и Q 4 в тепловом балансе сушилки незначительно, эти величины можно опустить. Тогда, определяя
Q 1 , Q 2 и Q 5 через параметры материала сушильного агрегата и наружного воздуха, записывая уравнение динамики в приращениях, вычитая соответствующее ему уравнение статики и линеаризуя полученное выражение, для первого звена окончательно получим:
dA fr a2----- + ax At = X;
2 dτ1
При этом x1 = AQ - gAto - bAB ;
a = Lcr + 0,47Bn + У F.k.; 1 Г 0
i = 1
a 2 = G ( C M + to 0 C B ) + P C c CT + VY r c r ;
A tHd g = ——mBn + GГ
A®H b = 595 + 0,47tr - CBtM +4^^^m (cM + Cb®o ), A»H где: PC - масса корпуса сушилки, кг;
dω
B = G--- - массовый расход испаряе-dτ мой из материала влаги, кг/ч;
A t H t 1 Г - t H
-
перепад температур в
пог-раничном слое у поверхности материала, °С;
t M , t Г - температура соответственно материала и воздуха (газа) в начале процесса, °С;
t п - температура поверхности материала, °С;
AWH = W1- WPABH - разность влагосо- держания, г/кг;
n - число зон, на которые разделяется сушилки при определении ее динамических характеристик;
RI - коэффициент теплопередачи в I-й зоне;
-
L - расход воздуха, м3/с;
-
V - объем сушилки, м3;
G - масса материала в сушилки, кг;
-
Y Г - плотность теплоносителя, кг/м3;
F - площадь поверхности теплообмена I-й зоны, м2.
Для сушилки непрерывного действия при малых AQ коэффициенты a1 и а2 в уравнении (2) можно считать постоянными, так как to0 = idem и B0 = idem, поэтому передаточная функция звена 1 имеет вид:
W 1 ( Р ) =
k 1
1 + pT 1
1 a где: k 1 = —, T 1= — . a 1 a 1
Постоянная времени T 1 характеризует инерционность сушилки как теплового объекта.
Вследствие изменений во времени величин ω 0 и B 0 , свойственных сушилкам периодического действия, коэффициенты a 1 и a 2 также являются функциями времени. Поэтому для таких сушилок передаточную функцию W 1 ( p ) можно рассматривать лишь как первое приближение. Однако в большинстве случаев данная передаточная функция достаточно точно описывает динамические свойства и сушилок перио-дического действия.
Звено 2 является безинерционным. При малых величинах отклонений от нормального хода процесса связь между изменением условий сушки материала, характеризуемых сигналом z, и отклонениями параметров воздуха - температурой в начале процесса A tr и влагосодержанием A d - может быть задана уравнением:
z = - h 1 A tr + h 2 A d . (7)
В сушилках непрерывного действия коэффициенты h 1 и h 2 - постоянные, а в сушилках периодического действия они являются функциями времени.
Звено 3 характеризует инерционность процесса влагообмена и описывается дифференциальным уравнением
т dAto , л
Tr--+ Ato = z,
C dτ ,
где TC = 1/ A .
Постоянная времени TC характеризует инерционность процесса сушки.
В сушилках непрерывного действия величина T C = idem и, следовательно, передаточная функция звена 3
W 3 ( p ) =
.
1 + PT
В сушилках периодического действия постоянная времени TC изменяется в процессе сушки, т.е. в этом случае передаточную функцию W 3( p ) можно рассматривать лишь как первое приближение. В литературе приводится выражение передаточной функции W 3 ( p ) с учетом зависимости TC от времени.
Звено 4 связывает изменение интенсивности выделения влаги A B из материала с изменением среднего влагосодержания и описывается уравнением:
A B = - G
d A to d τ
Его передаточная функция:
W 4( P ) =- GP .
Звено 5 определяет изменение расхода теплоты в зависимости от изменения интенсивности выделения влаги из материала и имеет передаточную функцию:
W 5 ( P ) = b . (11)
Звено 6 характеризует изменение расхода тепла, вызванное изменением влаго-содержания материала, и имеет передаточную функцию:
W 6( P ) = g . (12)
Для сушилок периодического действия:
dA tr A t„ g = G--Г- + —— mB .
d T A to H
Для сушилок непрерывного действия:
d A tr g = G j dτ
.
Принимая, что
τ
A tr = ( A tr )0[1 - exp(--)] , определим
τ 0
суммарный сигнал обратных связей хо.с через звенья 5 и 6:
x O . c = - ( g A to + b A B ) . (13)
Подставим выражение (13) значения A to , g и A B , получим:
1τ xOC = -Ght(Atr )0 —exp(—)(b-Atr) =-AB(b-Atг) τ0 τ0
Из полученного выражения следует, что влияние обратной связи через звено 6 (по A to ) может быть учтено небольшим уменьшением коэффициента усиления в звене 5.
Звено 7 связывает изменение влагосо-держания воздуха A d с отклонением интенсивности выделения влаги A B из материала и описывается дифференциальным уравнением:
TddAd + A d = k 7 AB, (14), dτ где: Td = V / N и k7 = 1000/ L ;
N - подача вытяжных вентиляторов.
Постоянная времени Td характеризует инерционность системы процесса смещения воздуха в сушильном пространстве.
Звено 8 связывает изменение относительной влажности A ^ с отклонением температуры A t г и влагосодержания A d воздуха. При малых отклонениях параметров уравнение звена имеет вид:
. (Ad .A ) z1{-x
AФ = Фо -,— 2I. (15)
у d о ( t г ) o )
При составлении математической модели конвективной сушилки принимаются следующие допущения:
-
1. Теплоемкости материла, влаги (воды), транспортирующего устройства и коэффициенты теплоотдачи от воздуха к материалу и транспортирующему устройству постоянны по длине и площади поперечного сечения сушилки, а также во времени. Кроме того, они не зависят от температур, а коэффициенты теплоотдачи и от расхода воздуха вследствие относительно небольших номинальных значений отклонений температуры и расхода.
-
2. Температура и влагосодержание материала распределены по длине аппарата и сосредоточены в его поперечном сечении (одномерная задача).
-
3. Поперечное сечение слоя материала
значительно меньше длины сушилки, а скорость воздуха намного больше скорости перемещения вдоль сушилки. Следовательно, время прохождения воздуха сквозь материал значительно меньше времени прохождения материала внутри сушилки. Относительное изменение параметров воздуха в сушилке, как правило, меньше относительного измерения параметров материала.
Заключение
Исходя из проведенных исследований, можно сказать, что математическая модель процесса сушки зерна в конвективных сушилках в одной зоне описывается пятью уравнениями: теплового баланса для зоны; мате- риального баланса (по влаге); теплообмена между зерном и влажным воздухом; сушки зерна; движения теплоносителя вблизи поверхности материала (алгебраическое).
Список литературы Математические модели сушки макаронных изделий
- Асамбаев А. Автоматизация технологических процессов для хлебопекарного, макаронного и кондитерского производства: Учебное пособие/Асамбаев А. -Астана: Фолиант, 2010. -384 с.
- Грачев Ю.П., Плаксин Ю.М. Математические методы планирования эксперимента. -М.: ДеЛи принт, 2005. -296 с.


