Математическое и программное обеспечение для повышения энергоэффективности протокола управления потоками данных со скрытой Марковской моделью в беспроводных сенсорных сетях

DOI:

Энергоэффективность является критическим фактором при проектировании и эксплуатации беспроводных сенсорных сетей (WSN). Из-за ограниченного срока службы батареи сенсорных узлов оптимизация потребления энергии имеет важное значение для продления срока службы сети. В этой главе представлена стохастическая модель на основе скрытых марковских моделей (HMM) для повышения энергоэффективности протоколов управления потоками данных. Предлагаемый подход фокусируется на снижении использования ресурсов во время передачи данных путем динамического выбора оптимальных путей на основе уровней энергии.

Основной проблемой в WSN является управление потреблением энергии при обеспечении надежной передачи данных. Традиционные протоколы часто не учитывают динамические изменения в условиях сети, что приводит к неэффективному использованию энергии. Для решения этой проблемы мы предлагаем стохастическую структуру, которая интегрирует HMM в процесс управления потоками данных, обеспечивая адаптивное принятие решений на основе наблюдаемых уровней энергии.

ТЕОРИЯ СКРЫТОЙ

МАРКОВСКОЙ МОДЕЛИ (HMM)

Скрытая марковская модель (HMM) - это стохастический метод, который продемонстрировал свою эффективность во многих областях [1, 2], таких как обработка изображений, распознавание цифровых отпечатков, классификация, сегментация ДНК [3, 4] и так далее. В нашем контексте формализм HMM [5], дающий хорошие результаты в указанных областях, адаптирован для реализации вероятностного протокола управления потоками данных. Насколько известно, этот метод впервые был использован в протоколе управления потоками данных.

Фактически, процессы реального времени производят наблюдения, которые могут быть дискретными, непрерывными, стационарными и изменяться во времени.

Основная трудность заключается в том, чтобы охарактеризовать наблюдения как случайные процессы, которые следует оценивать с помощью четко определенного теоретического подхода. Мы рассматриваем протокол управления потоками данных как дискретное событие, и его функции используются для определения скрытых событий как переменных марковской модели [6]. Идея состоит в том, чтобы оценить предположения о скрытых путях с помощью вероятностного скрытого марковского метода. Преимущества этого метода заключаются в том, что он требует меньше ресурсов, позволяет извлекать информацию из существующих параметров работы WSN и прогнозировать оптимальный способ передачи данных [7].

ОБОЗНАЧЕНИЯ

В таблице 1 приведены основные переменные, используемые в работе. Рассмотренные скрытые состояния представляют энергии различных путей и обозначаются символом E. Все эти обозначения повторяются в тексте.

Таблица 1. Обозначения HMM.

TABLE 1. HMM notations.

Обозначение	Описание
A	Вероятности перехода между состояниями
B	Матрица вероятностей наблюдения
M	Количество символов наблюдения
N	Количество состояний в модели
P	Распределение начальных состояний
S	Различные состояния марковского процесса (s 0 , s 1 , . . ., s N-1 )
T	Длина последовательности наблюдений
V	Набор возможных наблюдений (0, 1,..., M-1)
Y	Последовательность наблюдений (Y 0 , Y 1 , . . .,Y T-1 )
X	Контекстуальный набор скрытых состояний, Ω={S i }={E 1 , E 2 , E 3 }

ПАРАМЕТРЫ МОДЕЛИ

Модель HMM, обозначаемая λ , состоит из набора параметров, которые определяются следующим образом.

λ=(A, B, П)(1)

где

• •    Вероятности начального состояния П:

ni=[P(XI=EA)]i

где

^^i = 1(3)

• •    Матрица A переходов состояний:

A=aij=[P(X=E/X-i=Ea)]i j(4)

где матрица должна соответствовать следующему предположению:

£^ = 1(5)

Каждый элемент ац представляет собой коэффициент перехода между скрытыми состояниями.      Эмпирический      метод, используемый в этой работе для оценки начальных коэффициентов, описан в [8], значение переходных состояний зависит от энергии каждого пути.

• •    Матрица NxM вероятности излучения B=b j (v k )     представляет     вероятность

наблюдения в момент времени t символа v k при заданном состоянии E j .

• •    Последовательность           наблюдений

V=v 1 ,v 2 ,…,v M - это последовательность из М наблюдений, где v j ∈ {Низкий; Средний; Высокий}.

Символы наблюдений относятся к физическим характеристикам системы. В работе они состоят из оставшейся наблюдаемой мощности узлов для разных состояний и называются низким (L), средним (M) и высоким (H).

• •    Для простоты в остальной части текста мы используем обозначение i для E i , k для v k .

В следующем разделе приводится более подробная информация, относящаяся к предлагаемому     методу.      Описывается архитектура системы и марковская реализация.

ПРЕДЛАГАЕМАЯ АРХИТЕКТУРА

Предлагаемая архитектура в основном состоит из трех модулей, обозначенных пунктирными линиями на рисунке 1. Это проектирование сети, инициализация случайных параметров и поиск оптимального скрытого пути. Все эти шаги позволяют системе прогнозировать наилучшие параметры управления потоками данных.

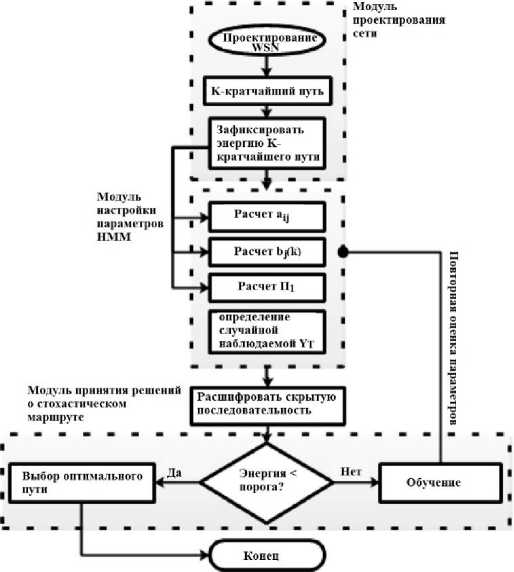
Рисунок. 1. CТРУКТУРА основных модулей общей системы стохастической управления потоками данных.

• Figure 1.    Structure of the main modules of the general system of stochastic data flow control.

  ОБЩАЯ СХЕМА СИСТЕМЫ

  
  

  10. EndIF.

  
  

Подход к минимизации энергопотребления в предлагаемом    стохастическом    процессе управления потоками данных проиллюстрирован на рисунке 1.

Первый модуль в блок-схеме позволяет наблюдать за поведением существующей сети и извлекать уроки из него. В этом блоке, функции управления потоками данных собираются на основе традиционных алгоритмов и извлекают соответствующую информацию. Второй модуль состоит из получения функций, подготовленных в первом модуле, для инициализации параметров скрытой адаптированной марковской модели. Он вычисляет их с помощью эмпирических формул. Третий модуль - это блок принятия решений, который позволяет выбрать оптимальный путь из числа k кратчайших, повторно оценить новые параметры в системе и найти более эффективный процесс управления потоками данных.

Алгоритм   1. Стохастический поиск кратчайшего пути

Требуется: G = (V, E).

Задача: Найти K-кратчайший путь.

• 1.    Общая энергия пути: Е_к = Y t= ₁c_ki .

• 2.    Общий вес пути: Cost_k = X ”=i cos t_k. .

• 3.    Вычисляем начальные параметры (A, B, Π).

• 4.    Фиксируем символы Y t для наблюдения за временными рядами.

• 5.    Применяем алгоритмы "Вперед-назад" и "Витерби".

• 6.    If Достигнуто Пороговое значение.

• 7.    Then Выбираем оптимальный маршрут.

• 8.    Else Обучаем модель.

• 9.    Возврат (3).

В алгоритме 1 K-кратчайших путей были вычислены с использованием процедур и уравнений, представленных в алгоритме Йена [9], на основе стоимости ребер. В строке 1 общее потребление энергии на каждом кратчайшем пути составляет E_k = £ p_ ₁e _k; . В строке 2 стохастическая модель инициализируется эмпирическим путем. В строке 3 используются уравнения (8) - (10) соответственно. В строке 4 используется уравнение (12), строка 5 соответствует уравнениям (13) - (20), а строка 7 соответствует уравнению (21).

Образец магистральной сетевой топологии, использованный для демонстрации модели, представлен в следующем разделе.

ПРИМЕРНАЯ ТОПОЛОГИЯ СЕТИ

Рассмотрим N сенсорных узлов, развернутых в прямоугольной области M x N, обозначенной как типовой граф G=(V, E) [10]. Здесь V={v 1 , v 2 , …, v n } представляет вершины количеством |V|, а Е={e 1 , e 2 , …, e m } представляет ребра между узлами датчиков количеством |E|. Путь или маршрут от узла-источника n i e V к узлу-получателю n j e V представляет собой последовательность узлов, выбранных протоколом управления потоками данных для пересылки данных. Link(i,j) e E включается в маршрут и оценивается с точки зрения энергозатрат, потребляемых содержащимися в сети узлами.

Рисунок. 2 используется в качестве демонстрационной модели для иллюстрации предлагаемой методологии. Узлы обозначены символами N k , где k - ссылка на узел в топологии.

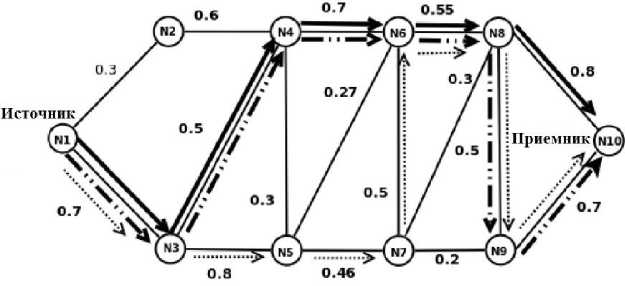
Рисунок. 2. Пример сетевой топологии, используемой для демонстрации протокола управления потоками

ДАННЫХ ПО СТОХАСТИЧЕСКИМ КРАТЧАЙШИМ ПУТЯМ :     РЕБРО ;    E 1 ( МАРШРУТ 1);      E 2 ( МАРШРУТ 2);      E 3

( МАРШРУТ 3).

• Figure 2.    An example of a network topology used to demonstrate the stochastic shortest path flow control

protocol:    edge;    e1 (route 1);       e2 (route 2);       e3 (route 3).

Простые линии обозначают общие ребра связи, жирные черточки, пунктирные стрелки и пунктирные стрелки-точки, обозначают рассматриваемые пути. Значения энергии всех связей (ребер), которые регистрируются с помощью работающей сети датчиков, находятся в диапазоне 0,2-0,8. Эти значения используются для инициализации параметров стохастической модели управления потоками данных HMM.

Пороговое значение энергии фиксируется на уровне 0,4 [11] для выбора ребер, участвующих в процессе управления потоками данных.

ЭМПИРИЧЕСКАЯ ОЦЕНКА ИСХОДНЫХ ПАРАМЕТРОВ HMM

Входные данные нашей системы используют численные значения энергий, показанные на предыдущем графе в качестве примера, для вычисления соответствующих коэффициентов на основе предложенного эмпирического подхода.

Формулы, используемые для получения начальных параметров системы, используют минимальное значение энергопотребления Emin в каждом канале. Каждый передаваемый пакет содержит минимальное количество энергии, необходимое для передачи информации по сети.

Минимальная энергия пути - это минимальное потребление всеми узлами на выбранном пути [11].

Ниже приведены формулы для инициализации модели.

£ min

^ ^l   у 32 mni n                     ⁽⁶⁾

4=lEj

aij = 1

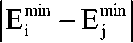
L( Emin - Emin) j min     min

E i   ^{- E}j

L( Emin - Emin) i,j=1

- ,i * j,Emin > Emin a ,         , i             j

,i * j,Emm < Emin

min      min

¹ - L ^aik^,i = ^k, E * E j k = 1

Уравнения (6) и (7) показывают стратегию, основанную на эмпирической энергии системы, для получения всех соответствующих коэффициентов.

Распределение в уравнении (8) получено в соответствии с традиционной стоимостью каждого пути.

( \cos t i ~COSt j \

7------------1—a , i * J, COS ti> COS tj \costl-2j=1costj\ bE^Vk) = ’

|coS t i -COS t j \ lcost_i-2 j= ₁cost j l

,i * J, COS t_l< COS t j

11 - H=₁b j (k),J = k,E j * V k

Уравнения (6), (7) и (8) должны учитывать предположения о вероятностях Маркова, выраженные в уравнениях (3) и (5).

ЗАКЛЮЧЕНИЕ

В статье представлена новая стохастическая модель управления потоками данных на основе скрытых марковских моделей (HMM), адаптированная для беспроводных сенсорных сетей (WSN). Интегрируя эмпирические данные из существующих сетей, модель предсказывает оптимальные пути посредством максимизации ожиданий, гарантируя динамические решения по маршрутизации, которые экономят энергию. Внедрение HMM не только снижает потребление энергии, но и продлевает срок службы сети как минимум на 19,05%, превосходя другие современные методы. Это методологическое достижение представляет собой значительный шаг вперед в оптимизации WSN, предоставляя надежную основу для будущих исследований и практических    приложений    в    области энергоэффективного управления потоками данных.    Успешная    адаптация    HMM подчеркивает его потенциал в повышении эффективности и устойчивости сети в различных процессах реального времени.