Математическое моделирование процесса экстракции водорастворимых веществ из хвои сосны. Часть 2. Оптимизация процесса

В первой части работы [1] нами была предложена кинетическая модель и определены значения констант скоростей (К), а также максимально достижимой концентрации водорастворимых веществ, извлекаемых из хвои сосны (Стах) при различных условиях проведения процесса. Эти данные положены в основу оптимизации процесса экстракции.

С практической точки зрения, целью оптимизации является выбор режимов, обеспечивающих максимально возможную степень извлечения с максимальной скоростью (за минимальное время). Поэтому в качестве оптимизируемого использовали параметр Y = К ■ C_max= f(R, D, t°) (Таблица 1).

Таблица 1. Оптимизация процесса экстракции хвои водой.

Из данных таблицы следует:

при D,t° = const - с увеличением размера частиц хвои параметр Y - уменьшается;

при R,t° = const - с увеличением дозы хвои параметр Y - увеличивается;

при D,R = const - с увеличением температуры - t° параметр Y изменяется экстремально с максимумом при t°= 65 °C.

Для наглядного представления данных закономерностей в виде поверхностей отклика необходимо их количественное описание. С этой целью для параметра - Y в качестве модели приняли уравнение множественной регрессии вида:

Y = ЬО + Ь1 ■ XI + Ь2 ■ Х2 + ЬЗ ■ ХЗ + Ь4 ■ ХЗ2              (1)

где ЬО, Ы, Ь2, ЬЗ, Ь4 - коэффициенты уравнения регрессии; XI - средний размер частиц - R, Х2 - доза хвои, ХЗ - температура экстракции.

Статистический расчет коэффициентов уравнения (1), осуществлялся в математическом пакете STATISTICA (версия 6.0). Использовали стандартную процедуру множественного линейного регрессионного анализа (методом наименьших квадратов с использованием t -распределения при доверительной вероятности 0,95).

Значения коэффициентов для уравнения (1) составили:

ЬО = -17,377; Ы = -0,0161; Ь2 = +0,1603; ЬЗ = +0,5444; Ь4 = +0,0043.

В таблице 1 приведены рассчитанные по уравнению (1) значения параметра оптимизации - Ypac4.

На рисунках 1а и 16 приведены поверхности отклика для параметра Y= K.Cmax, рассчитанные в соответствии с уравнением (1).

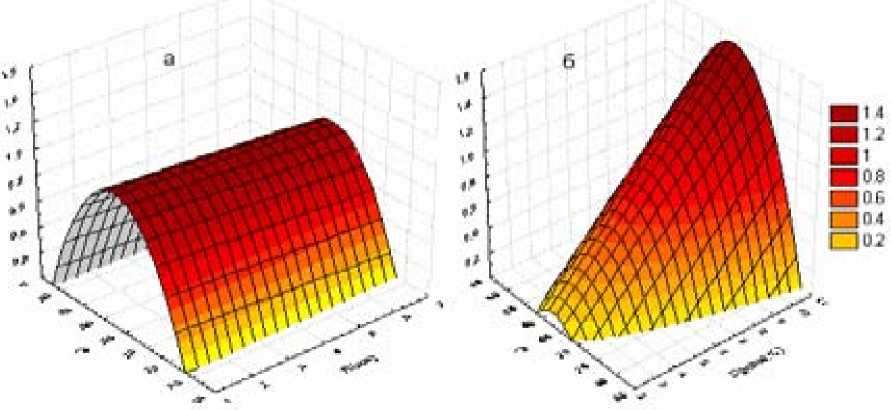
Рисунок 1. Зависимость предсказанных значений параметра оптимизации - Y_pac4 от: а - размера частиц хвои и температуры при D= const; б - дозы хвои и температуры при R= const.

Среднеквадратичное отклонение значений параметра оптимизации, полученных на основе экспериментальных данных, от рассчитанных по уравнению (1) составило 0,065 (12 %).

Таким образом, уравнение (1) удовлетворительно описывает экспериментальные данные и может быть использовано для предварительной оценки оптимальных входных параметров процесса экстракции хвои (в изученных пределах их вариации) и построения поверхностей отклика.

Из таблицы 1 следует, что величина Y имеет максимальное значение при D= 10 масс.%; Rcp-= 1,5 мм (0,1-3 мм) и t°= 65 °C. Оно же соответствует оптимальным условиям проведения процесса. Это позволило по значениям К и Стах по уравнению Ерофеева-Колмогорова при данных условиях оценить время, необходимое для достижения определенной степени извлечения в оптимальном режиме. Оно составило 15 минут при извлечении на 90 % и 45 минут - на 95 %. Поэтому на практике приемлемым является время экстракции - 30 минут.

Результаты и выводы:

Оптимизированы условия проведения экстракции водорастворимых веществ из хвои сосны: доза хвои - 10 масс.%, средний размер частиц - 1,5 мм (0,1-3 мм), температура экстракции - 65°С, продолжительность - 30 мин.