Математическое моделирование развертывания солнечной батареи с использованием уравнений движения в гамильтоновых переменных
Автор: Иванов В.Н.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (42), 2018 года.
Бесплатный доступ
Рассматривается задача математического моделирования процесса раскрытия солнечной батареи космического аппарата. В качестве расчетной схемы выбрана система связанных абсолютно твердых тел с замкнутыми кинематическими цепями. Представлена новая форма уравнений движения, в которой в качестве переменных, однозначно определяющих положение и распределение скоростей тел системы в пространстве, используются гамильтоновы переменные: обобщенные координаты и обобщенные импульсы. Цель настоящего исследования: на примере одной из конструкций солнечной батареи описать все этапы применения этих уравнений в процессе компьютерного моделирования динамики механических систем с замкнутыми кинетическими цепями.
Система абсолютно твердых тел, уравнения движения, динамика, математическое моделирование, солнечная батарея, кинематические связи, kinematic сonstraints
Короткий адрес: https://sciup.org/147245393
IDR: 147245393 | УДК: 531.01+004.94 | DOI: 10.17072/1993-0550-2018-3-31-38
Текст научной статьи Математическое моделирование развертывания солнечной батареи с использованием уравнений движения в гамильтоновых переменных
Рассматривается задача математического моделирования процесса раскрытия солнечной батареи (СБ) космического аппарата (КА). Очевидно, что без успешного завершения операции по раскрытию СБ в реальных условиях космического полета невозможно дальнейшее функционирование КА. Поэтому всесторонняя проработка всех этапов этого процесса и определение параметров конструкции, позволяющих успешно выполнить операцию развертывания СБ в различных штатных и нештатных ситуациях космического полета, является важной частью опытно-конструкторских работ при проектировании СБ.
Физическая стендовая имитация процесса раскрытия СБ в заводских условиях требует привлечения сложного и дорогостоящего экспериментального оборудования и создания полноразмерных опытных образцов СБ. Компьютерное моделирование на всех стадиях
разработки позволяет существенно снизить объем экспериментальных работ и, соответственно, уменьшить затраты на их организацию и проведение.
Различным подходам к решению поставленной задачи посвящено большое количество работ, некоторые из которых приведены в списке литературы [1–6].
В настоящей работе в качестве расчетной схемы математической модели выбрана система связанных абсолютно твердых тел (СТТ) с замкнутыми кинематическими цепями. Представлена новая форма уравнений движения СТТ, в которой в качестве переменных, однозначно определяющих положение и распределение скоростей тел системы в пространстве, используются гамильтоновы переменные: обобщенные координаты и обобщенные импульсы (импульсы Пуассона). Цель настоящего исследования: на примере одной из конструкций СБ описать все этапы применения этих уравнений в процессе компьютерного моделирования динамики механических систем с замкнутыми кинетическими цепями.
1. Описание механической системы
Для начала рассмотрим систему связанных абсолютно твердых тел со структурой дерева. Будем предполагать, что кинематические связи, реализуемые в шарнирах, голо-номны и идеальны.
Пусть N – число тел и шарниров в системе (не считая тела «0», движение которого во времени относительно инерциальной системы координат (СК) задано).
Пронумеруем тела и шарниры таким образом, чтобы для любого тела или шарнира в графе системы номер предшествующего ему тела или шарнира был меньше. В этом случае для полного описания структуры взаимосвязей в такой системе достаточно одного цело-
за переносное, в соответствии с правилом сложения скоростей можно записать рекуррентные формулы для вычисления проекций
линейной υi и угловой ω i скоростей тел ме-
ханической системы на оси i -й СК [7]:
v = Cv + Aq + v * (l)
i ik ii i
численного массива k = { k^ ,
...,
kN } , на i -м
месте которого расположен индекс тела или шарнира, предшествующего i -му. C каждым телом системы свяжем следующие множества: P i – упорядоченное множество индексов шарниров, составляющих путь между нулевым и i -м телами; U i – множество индексов шарниров, для которых i -е тело является предшествующим.
Введем следующие обозначения: ρ – матрица-столбец координат точки O i начала СК, связанной с i -м телом, в k -й СК; r – матрица-столбец координат точки O i в инерциальной СК; G i j – матрица направляющих косинусов между базисными векторами j -й и i -й систем координат (матрица преобразования координат из j -й СК в i -ю).
Введем матрицы-столбцы обобщенных
координат q i = ( q l ,
...,
nT q11) , параметризую-
щих уравнения связей каждого i-го шарнира, n – число обобщенных координат. Матрицы p и G = G1 являются функциями обобщен- i ik i ных координат:
P i = P i ( q i , t ) , G i = G i ( qi, t ) .
Введенные матрицы связаны между собой рекуррентными формулами:
r = r^ + G 00 P i , G 0 = G 1 G 0
.
Принимая движение i -го тела за относительное, а предшествующего ему k i -го тела
I U где v = 1
1 k 0
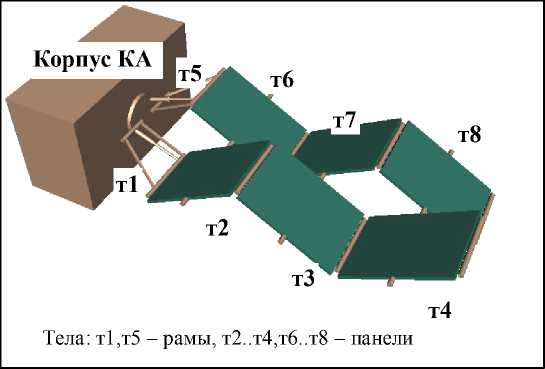
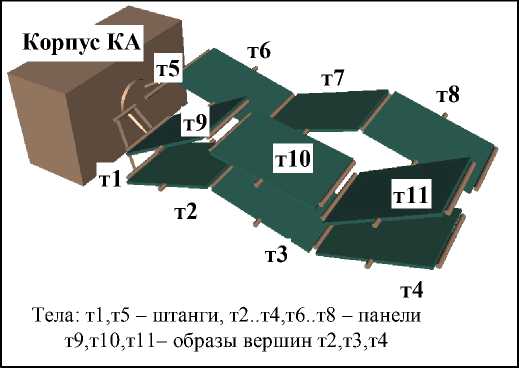
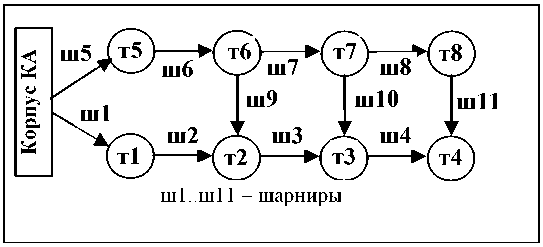
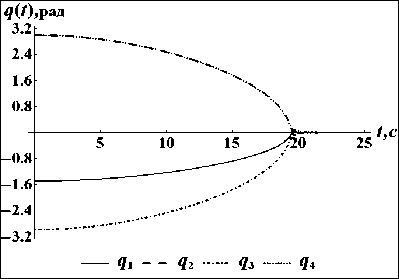
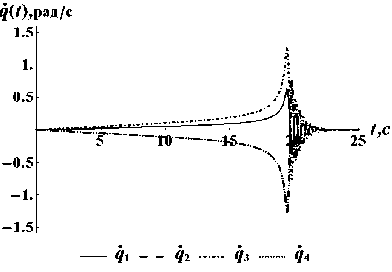
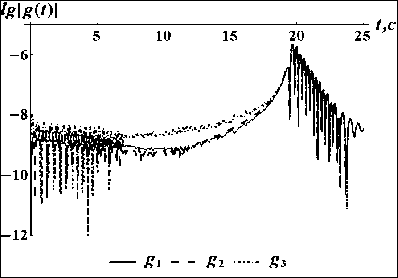
U d aij = Gi , 1j 1d q{ - r d GT 0 = G J, 1 1dt , * vi υi* * U1. k 01 ) , Ai = =G1%, dt J = l, n, C1 =( G1 k aυi1 aiω1 . . . ... a 0=G1 —G1P1 Gi υ an a0 ) d GT , dql , Здесь и далее символ «~» используется для обозначения кососимметричной матрицы (это соответствует матричной записи векторного произведения [7]). Введем блочную 6N×6N-матрицу S с квадратными подматрицами порядка 6 по следующей формуле: S ■ = 1j E6, - C1, 06x6, J =1, ____ J = k1, 1, J = l, N. (2) j *1 v k1, Заметим, что для любой кинематической структуры эта матрица содержит в каждой строке только два ненулевых блока E6и - C1. Поскольку матрица S содержит информацию как о топологической структуре системы, так и об относительном положении тел в системе, ее называют матрицей кинематической структуры. С использованием матрицы S уравнения кинематики системы тел (1) можно записать следующим образом: STv = Aq + v *, (3) где A = d1ag(Ai,...,An), q=(qi,...,qN) , v = (vi,...,vn)T. Рекуррентные формулы (3) можно записать в виде явных выражений v = T (Aci + v *), (4) где обратная к S матрица T = S 1является блочной 6N×6N-матрицей, подматрицы которой могут быть вычислены по рекуррентным формулам: E6, T = < С Т, ■ / 1"l J J, I 06x6, J =1, ____ J e P1, 1, J = l, N. J £ P1, 2. Уравнения движения СТТ со структурой дерева в гамильтоновых переменных Пусть mi – масса i-го тела; Ji – тензор инерции i-го тела; ric – матрица-столбец проекций радиуса-вектора центра масс i-го тела на оси связанной с ним СК; fio , mio – проек- ции главного вектора и главного момента активных сил, действующих на i-е тело в i-й СК; Q – матрица-столбец обобщенных сил. Для математического моделирования раскрытия СБ используем расширенную форму уравнения движения СТТ со структурой дерева в гамильтоновых переменных [8]: Mv - ST ц = 0, -- STv + Aq = - v *, (6) AT Ц = P, p = ( AT - ATо) ц + Q. (7) Здесь введены следующие обозначения: M = diag (M i,..., Mn ), О = diag (Oi,..., О n ), Q = ATTTF, F = (Fi,...,Fn)T, Fi=(f0,mO)T, Mi = f mtE c < mi Г -miri Ji J О i = ωi ~ υi 0 ωi Особенность уравнений (6), (7) состоит в том, что они разрешены относительно производных обобщенных импульсов p (импульсов Пуассона). Первые три уравнения (6) образуют линейную систему с симметричной, блочной трехдиагональной разреженной матрицей коэффициентов относительно скоростей v, q и переменных ц, которые являются множителями Лагранжа. Полный вывод уравнений движения в форме (6), (7) можно найти в работе [8]. 3. Уравнения движения СТТ с замкнутыми цепями в гамильтоновых переменных Структуру механической системы можно представить в виде графа, вершины которого есть тела системы, а ребра – шарниры. Этот граф назовем первичным графом. Первичный граф всегда можно превратить в граф со структурой дерева (вторичный граф) путем размыкания замкнутых контуров. Размыкание проведем с помощью раздвоения в каждом замкнутом контуре одной из вершин первич- ного графа. При этом одну и ту же вершину можно раздваивать произвольное число раз. При раздвоении все образы одной вершины остаются не связанными непосредственно между собой и принадлежат к различным ветвям приведенной системы (вторичного графа). В приведенной системе существует соответствие между образом и прообразом раздвоенной вершины. Соединим пунктирными ребрами все такие пары вершин вторичного графа. Массово-инерционные характеристики раздвоенных вершин первичного графа и действующие на них внешние силы необходимо произвольным образом распределить между дополнительными вершинами вторичного графа. Пронумеруем тела и шарниры вторичного графа в соответствии с введенной выше правильной нумерацией вершин СТТ со структурой дерева. Пусть теперь N – число вершин вторичного графа и массивы k , P , U характеризуют структуру вторичного графа. Ведем матрицу s = (sj.), число строк которой соответствует числу дополнительных замкнутых циклов, а число столбцов совпадает с числом вершин (тел) во вторичном графе системы. Пусть s. = 1, если j — номер вершины в первичном графе системы, принадлежащей i-му замкнутому циклу, s = -1, если j - номер ij вершины во вторичном графе системы, являющейся образом соответствующей вершины первичного графа и принадлежащей i-му замкнутому циклу, s = 0 во всех других случаях. ij Будем считать, что СК, связанные с образами и прообразами раздвоенных вершин, расположены в телах одинаково. Тогда абсолютные координаты и скорости всех точек прообразов и образов раздвоенных вершин, спроектированные на связанные СК, должны совпадать. Это означает, что условия замкнутости кинематических цепей накладывают на движения вершин вторичного графа следующие кинематические и геометрические связи (ограничения): sv = sT (Aq + v * ) = 0, sn = s [ vdT = 0, 0 где n = j vdr - квазикоординаты. Ограничения (8), (9) очевидно являются зависимыми, поэтому при выводе уравнений движения будем учитывать только связи (9) на квазикоординаты. Модификацию уравнений движения (6), (7) можно выполнить, используя принцип Гамильтона–Остроградского [7]. При этом геометрические связи (9) учтем с помощью множителей Лагранжа η. Опуская выкладки, выпишем систему дифференциально-алгебраических уравнений в гамильтоновых переменных, которые вместе с уравнениями связей (8), описывают динамику СТТ с замкнутыми кинематическими цепями: Mv - ST ц = 0, <- STv + Aq = - v *, (10) AT Ц = P, p = ( AT - AT о) ц + AtTt (F + sTn). (11) Для определения множителей η будем использовать метод модифицированных функций Лагранжа [9, 10]. В этом случае уравнение (11) преобразуется к виду: p = ( AT - AT О) ц + ATTTF --ATTTsT (C (sn + u) + Dsv), где C, D – положительные диагональные матрицы коэффициентов жесткости и демпфирования колебаний невязок связей επ вокруг тривиального решения, u – вектор модифицированных множителей Лагранжа, компоненты которого можно рассматривать как управляющие параметры ПИД-регулятора. При этом множители η и u связаны соотношением n = -Cu. Тогда вместо второго из уравнений (11) для замыкания уравнения (12) можно использовать линейные дифференциальные формулы для пересчета управлений u ПИД-регулятора: u = k sn + k sv, (13) πv где k , k – коэффициенты усиления обрат-πv ной связи по нарушению ограничений (8) и (9). Уравнения (10), (12) и (13) образуют замкнутую систему дифференциальноалгебраических уравнений динамики СТТ с замкнутыми цепями в гамильтоновых переменных. Выбор параметров ПИД-регулятора. Настройка управляющих слагаемых в уравнениях (12), (13) заключается в подборе четырех векторных параметров k , k , С и D. Приме-πv ним следующий подход. Пусть на механическую систему накладывается только одна дополнительная связь (9). Если из системы уравнений (12), (13) исключить компоненты вектора состояний механической системы, удалить внешнее силовое воздействие, а затем линеаризовать эту систему и продифференцировать, то получим линейное однородное ДУ, описывающее собственные колебания модифицированного множителя Лагранжа u : u + sTAM “1 ATTTsT (Du + ( (14) +C (1 + kv) u + Cknu = 0, где M = ATTTMTA . Потребуем, чтобы характеристическое уравнение для ДУ (14) имело вид: (k + во)[ k + (в1 + iv)][ k + (в1 - iv)] = 0, (15) где β0, β1– коэффициенты демпфирования, ν – круговая частота регулятора. Предположим, что v2> v]2iax- в\ , в0 = p0vmax , в1 = pvmax , p0,1 = O(1), т. е. время переходного процесса в системе управления должно быть меньше, чем период наивысшей частоты колебаний механической системы. Сопоставляя характеристическое уравнение для ДУ (14) и уравнение (15), получаем следующие параметры ПИД-регулятора: ( sTAM-1( sTA )T D = ( P0 + 2P1) vmax, (sTAM!-1(sTA) T )c = vmax, (16) kn = P 0v max, kv = 2P 0 P1. Равенства (16) задают коэффициенты усиления обратной связи, демпфирующие и упругие параметры ПИД-регулятора (13). С практической точки зрения преимущество системы уравнений (10), (12), (13) заключается в том, что она имеет ту же структуру, что и исходная система (6), (7) без дополнительных связей. Это означает, что для ее разрешения относительно ускорений можно использовать те же методы, что и для исходной системы уравнений (6), (7). В работах [11, 12] получены алгоритмы метода прогонки и Холецкого разрешения системы уравнений (6), (7) относительно старших производных. В настоящей статье для разрешения системы уравнений (10), (12), (13) используется метод прогонки. Уравнения построены таким образом, что при возникновении отклонений επ изменяется в первую очередь ненапряженная длина дополнительного упруго-демпфирующего элемента C (sn + u) + Dsv так, чтобы создаваемая этим элементом дополнительная сила обеспечивала скольжение механической системы по дополнительной связи επ . 4. Решение уравнений движения СТТ методом прогонки Метод прогонки по существу является модификацией метода Гаусса решения систем линейных алгебраических уравнений с ленточной структурой. В данном методе при прямом ходе, который выполняется начиная с последнего тела системы, из группы уравнений (6) исключаются множители Лагранжа µ. При обратном ходе по явным формулам вычисляются последовательно для каждого тела системы обобщенные скорости с/, декар-товые скорости v и множители Лагранжа µ. Вывод рекуррентных формул метода прогонки подробно изложен в статьях [11, 12]. Здесь же приведем только результирующий алгоритм метода. Алгоритм метода прогонки for i = N :1 M * = M +y C^HM * C jeU j j j j D = AtM * A for i = 1: N q = D p - AT i i cp + m i i n = v i i v = Cv + Ac/ + v * i ik ii i и = M v + m i i i i end ll = k sn + k sv πv for i = N :1 F* = F + У s |C (Ул Л + u 1 + i i j ji j k jk k j D У S ,v,\ + Y . CTF* j^k jk k) j-UeUi j j p =(AT - ATq)и + ATF* i \ i i i / i i i end Трудоемкость решения с помощью данного алгоритма растет по линейному закону в зависимости от числа тел в механической систем. При реализации этого алгоритма требуется обращение только симметричных положительно определенных матриц ATM*A , порядок которых равен числу степеней свободы в i-м шарнире, причем эти матрицы симметричны и положительно определены, а их порядок всегда мал (не превышает шести). Именно этим и обусловлена эффективность этого метода. 5. Моделирование раскрытия СБ Описанную выше методику применим для математического моделирования процесса раскрытия одной из конструкций солнечной батареи (СБ), в конфигурации которой есть замкнутые цепи. Пусть СБ состоит из двух подобных цепочек солнечных панелей, соединенных в виде параллелограммного механизма (пантографа). Каждая цепочка есть многозвенный физический маятник, звенья которого соединены одностепенными вращательными шарнирами. На рис. 1 показаны фазы во времени раскрытия СБ. Расчетная схема СБ с тремя замкнутыми контурами, размещенная на КА, представлена на рис. 2. СБ содержит шесть однотипных солнечных панелей, соединенных с КА двумя рамами. В соответствии с методикой, проведем размыкание замкнутых контуров раздвоением подходящих вершин первичного графа. На рис. 3 представлена схема СБ со структурой дерева, полученная после раздвоения трех панелей первой цепочки СБ. Соответствующие расчетным схемам первичный и вторичный графы с замкнутыми цепями и со структурой дерева представлены на рис. 4 и 5. 0 c 8 c 24 c 16 c Рис. 1. Фазы во времени раскрытия СБ с конфигурацией в виде пантографа Рис. 2. Схема СБ с конфигурацией пантографа Рис. 3. Схема модели СБ с раздвоением вершин Рис. 4. Первичный граф СБ с замкнутыми цепями т9 т10 ш2 ш3 т2 т3 т6 ш6 ш7 ш9 ш11 ш4 т4 ш1..ш11 – шарниры Рис. 5. Вторичный граф СБ со структурой дерева Масс-инерционные характеристики вершин первичного графа разделим поровну между образами и прообразами раздвоенных вершин вторичного графа. Исходная механическая система имеет одну степень свободы. После размыкания замкнутых контуров система уже имеет 11 степеней свободы. В качестве обобщенных координат выберем относительные углы между последовательными звеньями СБ. Подготовим элементы уравнений движения. Структура вторичного графа системы задается вектором k = ( 0,1,2,3,0,5,6,7,6,7,8). Системы координат (СК), связанные с панелями, выберем в их центрах симметрии. В каждой СК ось Oz направлена перпендику- лярно плоскости соответствующей панели, а ось Ox параллельна оси вращения в шарнирном соединении. ki Пусть r i , r – радиус-векторы i-го шарнира в ki-й и i-й СК соответственно, q – относительные углы развертывания тел СБ (обобщенные координаты). Тогда матрицы направляющих косинусов между базисными векторами СК и радиус-векторы центров СК в предыдущих СК имеют вид (i = 1,...,11) : G = 0 i cosq .0 sin qi kTi р = ri - G r . i i i i 0 - sin q cos q < ^i J Элементы матриц A и С вычисляются по формулам (1). Матрица структуры дополнительных связей тел вторичного графа системы, вызванных замкнутыми циклами, имеет вид: (0 1 0 0 0 0 0 0 -1 г= 00100000 0 ^0 0010000 0 0 0 л -1 0 0 -1J В исходном положении панели СБ компактно сложены и зафиксированы на корпусе КА (рис.1). Начальные условия на обобщенные координаты в начальный момент интегрирования задаются вектором q(0) = (-pп, —П,n,p-п,п,-п,п,-п,пл. При раскрытии батареи происходит перевод батареи в конечное (раскрытое) рабочее положение q (t) = 0 и фиксация батареи в нем. Пружины кручения, расположенные в шарнирах и отвечающие за распахивание звеньев СБ, моделируются линейными упру-го-демпфирующими элементами. В силовой характеристике каждого упругого элемента учитывается предварительный угол закрутки пружины кручения. Когда угол раскрытия смежных звеньев в i-м шарнире достигает конечного значения q (t) = 0, происходит фиксация соответст- вующего звена на упоры. Фиксация звеньев также моделируется упруго-диссипативными моментными силовыми элементами с большими значениями коэффициентов жесткости и демпфирования, чем в рабочих пружинах кручения шарниров. В результате численных расчетов в среде САВ Mathematica были получены графики изменения во времени обобщенных координат, скоростей всех звеньев СБ и невязок в дополнительных связях. На рис. 6, 7 приведены графики обобщенных координат и скоростей первых четырех звеньев СБ, входящих в первую цепочку. Результаты для второй цепочки панелей СБ идентичны. На рис. 8 в логарифмическом масштабе представлены зависимости длин невязок дополнительных связей |g (t )| = |гп( t )|, обеспечивающих замыкание параллелограмм-ного механизма СБ и вызванных действием управляющих воздействий ПИД-регуляторов. Графики на рис. 8 характеризуют достигнутую точность численного моделирования. Отметим, что на всех рисунках можно выделить характерные области. Например, участок постепенного изменения координат и скоростей вследствие работы пружин кручения и участок ударного срабатывания механизмов фиксации панелей и последующих затухающих колебаний элементов конструкции СБ. Рис. 6. Угловые координаты в шарнирах Рис. 7. Угловые скорости в шарнирах Рис. 8. Порядки невязок связей Заключение В статье описаны методы формирования математических моделей систем твердых тел с замкнутыми кинематическими цепями с использованием уравнений движения в гамильтоновых переменных. Представлены алгоритмы численного моделирования подобных механических систем. Приведены все этапы компьютерного моделирования процесса раскрытия солнечной батареи, в конфигурации которой содержатся замкнутые цепи с использованием описанной методики.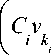
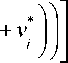



Список литературы Математическое моделирование развертывания солнечной батареи с использованием уравнений движения в гамильтоновых переменных
- Бушуев А.Ю., Фарафонов Б.А. Математическое моделирование процесса раскрытия солнечной батареи большой площади // Математическое моделирование и численные методы. 2014. № 2 (2). С. 101-114.
- Борзых С.В., Ильясова И.Р., Щиблев Ю.Н. Динамика раскрытия крупногабаритных солнечных батарей // Космонавтика и ракетостроение. 2012. № 4 (69). С. 89-99.
- Еремин Л.И., Пугач И.Ю., Минчакова Е.П. Уточнение математической модели процесса раскрытия батареи фотоэлектрической с учетом влияния податливости шарнирного узла и нелинейности его жесткостных характеристик // Вопросы электромеханики. Труды ВНИИЭМ. 2017. Т. 158, № 3. С. 3-6.
- Крылов А.В., Чурилин С.А. Моделирование раскрытия солнечных батарей различных конфигураций // Вестник Московского государственного технического университета им. Н.Э. Баумана. Серия: Машиностроение. 2011. № 1. С. 106-112.
- Зимин В.Н., Крылов А.В., Мешковский В.Е., Сдобников А.Н., Файзуллин Ф.Р., Чурилин С.А. Особенности расчета раскрытия крупногабаритных трансформируемых конструкций различных конфигураций // Наука и образование: научное издание МГТУ им. Н.Э. Баумана. 2014. № 10. С. 179-191.
- Ручкин Л.В., Ручкина Н.Л. Моделирование трансформируемых механических систем // Сибирский журнал науки и технологий. 2017. Т. 18, № 4. С. 820-824.
- Лурье А.И. Аналитическая механика. М.: Гос. изд-во физ-мат. лит., 1961. 824 с.
- Иванов В.Н., Полосков И.Е., Шимановский B. А. Математические модели систем связанных твердых тел в импульсах Пуассона // Фундаментальные исследования. 2016. № 10-3. С.493-499.
- Иванов В.Н. Применение метода модифицированных функций Лагранжа для учета дополнительных связей в механических системах // Вестник Пермского университета. Математика. Механика. Информатика. 2013. Вып. 4 (23). С. 19-28.
- Иванов В.Н., Полосков И.Е. Метод модифицированных функций Лагранжа в задаче моделирования механических систем с дополнительными связями // Современные наукоемкие технологии. 2016. № 10-1. С. 67-73.
- Иванов В.Н., Шимановский В.А. Численные методы формирования и решения уравнений движения в импульсах Пуассона систем твердых тел со структурой дерева // Современные наукоемкие технологии. 2017. № 10. С. 13-18.
- Иванов В.Н. Алгоритмы решения уравнений движения в импульсах Пуассона систем твердых тел со структурой дерева // Вестник Пермского университета. Математика. Механика. Информатика. 2017. Вып.4(39). C. 25-31.


