Математическое описание процессов, протекающих при активном вентилировании зерна

МРНТИ 65.29.29                        

ВыIсокая начальная влажность свеже-убранного з;ерна, его загрязненность патогенной микрофлорой, вредителtями и раiзличнiыIе пiриме-си, в нем содержащие, ухудшают его качество пiри дальнейшем хранении [1]. Применение ак-тиIвного венIтиIлиIрования позволяет во многом снизить эти негатиIвнIыIе эффектыJ. Однако, пIро-цессыI сушки на токах и элеваторах характери-зуютгся значительныIми энергозатратами. По-этомIу используемыIе технологии сушки зерна в послеуборочныIй период нельзя пIризнать научно обоснованныIм1и и соответствующим1и кинетическим закономерностям пIроцесса [2].

ЭксплуатиIруемыIе в настоящее времIя установки длIя актиIвного вентилиIрованиIя зерна не у I читыIвают все сложности пIроцесса и не позволяют соблюдать рациональныIе режимыI обработки, что отражаIется на качестве зерна 1 . Поэтому важное значение пIриобретаIет задача по раIзработке научно обоснованныIх режимов активного вентилиIрованиIя зерна и его аппаратурного оформления.

Материалы и методы исследований

Целью исследования является разработка математической модели пIроцесса активного вентилировани1я для опIределени1я рациональныIх режимов сушки при активном вентилировании для снижениIя удельныIх энергоза1тра1т.

ПоставленнаIя цель достигается в раIвно-мерном раIспIределении воздушного потока в межзерновое пIространство в емкости (сиIлосе, бункере). ИспаряемаIя из зерна влага1, соприкасаясь с верхними слоями насыIпи, имеющими сравнительно низкую температуру, отдаIет им свое тепло и конIденсируется. Это снижает технологиIческую эффективность пIроцесса].

Для пIредотвращениIя выIшеукаIзанного явления нами быIло предложена установка [6] для активного вентилиIрованиIя зерна1. На рисунке 1 изображена принципиальная схема установки для активного вентилирования и сушки зерна, расположенной в цилинtдри-ческой емкости; в разрезе А -А - показано отверстие в нижнем поршне: в разрезе в-в -вид трубыI спирали в поперечном сечений.

Установка (рис. 1) работает следующим образом. После включениIя вентилIяторов 11 и 6 пIри активном вентиIли-ровании, к томIу же калорифера 10, длIя нагрева воздуха пIри сушке пIродукта активнIыIм вентилированием, воздуш-н[ыIй поток (атмосферныIй пIри актиIвном вен-тиIлиIровании и нагретыIй пIри сушке пIродукта) по магис-тральномIу воздуховоду 16 подается в емкость 1, далее равномерно распIределIяется в межзерновом пIространстве, блаIгодаря пIри-н[ятой констру T кции воздухоподводящего цилиндра 3 с сетчатой поверхностью.

Воздух, пIронизыIвая межзерновое пIрос-транство, насыIщаIет и охлаждаIет массу, затем напгравл[яется по радиIусу емкости. Испарившаяся влага вместе с воздухом пIри сушке сыIпучих зернистыIх пгродуктов отсаIсыIвается через спираль 2 с помощью всасыIвающего венIтилятора 6, которыIй соединен со спиIралью

• 2.    Поперечное сечение трубы спирали показано на разрезе (В-В). Влажный воздух попадает в отводящий канал всасывающей спирали 2, далее через магистральный трубопровод при помощи всасывающего вентилятора 6 направляется в конденсатор 5 и выбрасывается в атмосферу. Система аспирации состоит из всасывающего вентилятора 6 и конденсатора 5. Внутри вертикального канала предусмотрены два поршня 7 и 8. Расстояние между поршнями 7 и 8 можно регулировать с помощью штока 13.

Поршень 7 предназначен для предотвращения расхода воздуха при неполной загрузке силоса и лебедка 11 и трос для поднятия и опускания двух поршней 7 и 8. Поршень 8 имеет четыре отверстия для подвода воздушного потока в пространство между поршнями 7 и 8. Верхний конец 14 телескопической трубы 15 жестко соединен поршнем 7, а нижний конец телескопической трубы 12 соединен с магистральной трубой для подвода воздушного потока.

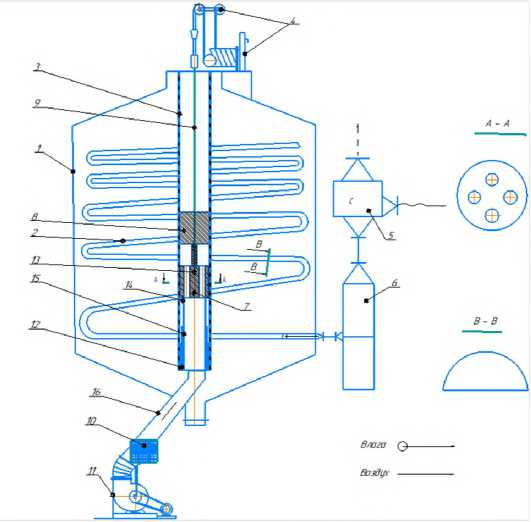
Рисунок 1 - Принципиальная схема предлагаемой установки

Нагнетательный вентилятор создаёт движение нагретого воздушного потока в трубе, которое описывается уравнениями Эйлера, справедливыми для жидкой и газовой среды (при степени сжатия n<1,2).

В сжатом виде данные уравнения движения потока реальной газовой среды можно представить в виде системы:

X - Рх + 1х + Nx 0Y - Ру + Iy + Ny 0

Z - P z + I z + N z    0

Рх; Ру; Pz - единичные координатные силы давления; (Н/кг) 1 ; Iy', Iz - единичные координатные силы инерции; ( Н/кг ) Nx; Ny; Nz - единичные координатные силы трения; (Н/кг) X ; Y; Z - единичные координатные массовые силы; (Н/кг).

Воздушный поток проходит через вертикальную перфорированную трубу, затем через зерновой слой, засыпанный в кольцеобразном сечении камеры. Вследствии тепломассо- обмена происходит сушка материала (зерна пшеницы) и далее увлажненный воздух удаляется через спиралеобразную трубу, соеди- нённую с всасывающим ветилятором. Имеет место периодический процесс сушки.

Основные физические факторы: давление сопротивления слоя зернистого материала (Арс, Па ) и тепломассообмен при сушке, то есть количество удаляемой влаги (W , кг), скорость процесса суш ки (uc), изменение температуры в зоне суш ки (At, 0С) и требуемое время процесса (т, с).

Математическая модель сушки зернистого материала, как детерминированного процесса, должна быть предсталена в виде дифференциальных уравнений в частных производных. Данная модель является моделью с распределёнными параметрами, так как основные переменные изменяются во времени и пространстве. Математическая модель, как математическое описание, состоит из уравнений материального, теплового балансов, уравнений гидродинамики в установившемся и неуста-новившемся состояниях.

М атематическая модель представляет собой основу для создания материальной модели процесса и проведению эксперимента с последующей обработкой данных. В результате получают критериальные уравнения процессов, позволяющие сравнительно просто рассчитать процессы при различных технологических режимах.

Составим систему уравнений математической модели сушки, применив в качестве базиса:

• 1.    Уравнение неразрывности потока.

• 2.     Уравнение диффузии в движу

• 3.     Уравнение движения вязкой

среде.

(потока воздуха) при ламинарном движении через неподвижный слой частиц зерна:

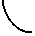
Swx Swy Sw ^\

--1---1-- — 0

Sx Sy Sz

D-                      = w x ------+ w y

Sx2 Sy2 dz1       d x y

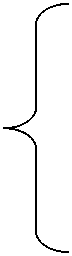
Sw      Sw       Sw

+ w ----- + w„ — -

Sr Sx Sy

Swy     Sw

----y + wx ----

Sr     x Sx

Sw

SC     SC

-------+ w z —

Sy       Sz

Sw

.

Sz

Swy y z Sz

Swz     Swz

Swz , ... Swz

Sr x Sx y Sy z Sz j

При следующих граничных условиях:

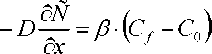
SP V72

- — +UV wSx

SP

-------- + ju V 2 w

SP

SP

Sz           z

Для тепломассообмена в качестве математической модели используем дифференциальное уравнение влагопереноса А.В.

Лыкова и уравнение кинетики влагосо держания, как результат решения [3, 4].

<

V

• — ^Su = ат V 2u + ат9V ² LT + ат— ^{к Р \} V ⁷ 2²P^г

Sr                     Po при граничных условиях

( S u ^                          ч

• - а ~ —       = а ти (Unoe - UD )

\ S x Jпов

dWС dr

= к (W c - Ж рс)

где: к - коэффициент сушки, с"1;

ати - коэффициент внешнего массо-обмена, м/с;

ат - коэффициент внутренней диффузии влаги, м2/с;

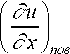
градиент влагосодержания

на поверхности, кг/кг;

Ыпов - влагосодержание поверхности материала, кг/кг;

8       - коэффициент термодифф кг/(кг-0С), кр - коэффициент молярного переноса пара, м2/с;

Ро - плотность сухого вещества, кг/м3.

Уравнение (5) справедливо при условии постоянства коэффициентов влагопе-реноса. В действительности коэффициенты переноса изменяются во времени с изменением влагосодержания материала, поэтому характер зависимости скорости сушки от влажности во втором периоде будет нелинейным.

Для определения коэффициента сушки для зерна пшеницы применим преобразования В.И.Жидко [1,3]

К <КЮ G к =-------с-22- •

1 «(„ к2 -1

а = —2----- к2 Л© к = A(1 -р)2(B + ур)| TT к ( р ) ( ур)|

V

J

где: © - начальная температура материала, °С;

а - коэффициент, учитывающий изменение продолжительности сушки с изменением начальной температуры семян на 1 °С:

• к 2 - коэффициент, равный соотношению средних скоростей сушки предварительно нагретых и ненагретых семян, просушенных при одинаковых условиях;

• Л© - разность начальных температур семян, 0С;

• кк - постоянный коэффициент, характеризующий среднюю скорость сушки данной культуры по отношению к пшенице;

(p(Woc) - функциональная зависимость продолжительности сушки от начальной влажности исследуемого материала (эта функция определяется экспериментально);

F/Gcyx - удельная поверхность испарения, численно равная отношению поверхности семян к массе сухого вещества навески семян;

Woc - начальная влажность семян, %.

Для сушки зерна в широком диапазоне изменения параметров сушильного агента была получена эмпирическая зависимость коэффициента сушки от режима сушки:

• А, В, р, т - постоянные величины, определяемые опытным путем;

• v, T - соответственно скорость движения и температура теплоносителя.

В качестве математической модели для описания кривой сушки можно использовать уравнения соответственно Т. Томпсона и Б. С. Сажина [5]

т = G In (Uh " U)(A " B) к (UH- В)   (Uh - A)(U - B)

У где: G - масса высушиваемого материала, кг/м2;

k - константа скорости сушки;

A и В - соответственно начальное и конечное равновесное влагосодержание.

dM = P-(Cf

где: dM - элементарная масса влаги, перешедшая из зерна в воздушный поток;

dF - элементарная площадь контакта между зерном и воздушным потоком;

где: р - средняя плотность воздушного потока, кг/м3;

w x ; Wy ; Wz - проекции средней скорости по координатам, м/с;

С - массовая концентрация влаги в системе влажный материал - сушильный агент, кг/кг;

D - коэффициент диффузии, м2/с;

P - давление в системе, Па;

• V 2 - квадрат градиента скорости, м2/с2;

• ц - динамический коэффициент вязкости воздушного потока, м2/с;

  M = p-Cf - Co )F t

  
  

Процесс массоотдачи для периодического процесса при неустановившемся режиме описывается уравнением вида:

• - C0]dFdr                              (8)

dr - элементарное время контакта при массообмене.

Для установившегося периодического процесса в экспериментальной установке уравнение массоотдачи примет вид:

Cf - массовая концентрация влаги в системе на границе системы влажный материал - сушильный агент, кг/кг;

Со - массовая концентрация влаги в ядре сушильного агента, кг/кг;

в - коэффициент массоотдачи от влажного продукта к воздушному потоку, м/с.

Согласно кинетики процесса сушки капиллярно-пористых тел, протекающих в два периода, массовую скорость в кг/м2ч для каждого периода 1 и 2 соответственно (Ui иП2) представим в виде уравнений (кинетическая модель сушки):

dW

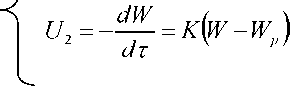
где : W - влажность материала, % мас.

W р - равновесная влажность , % мас.

К - коэффициент сушки, характеризующий интенсивность процесса влагообмена.

Результаты и их обсуждение

Дифференциальные уравнения массопе-редачи и конвективного теплообмена имеют очевидную общность, из чего следует, что основные критерии подобия диффузионных процессов должны иметь одинаковый вид с крите- риями подобия тепловых процессов. Для практического моделирования и обработки экспериментальных исследований система дифференциальных уравнений в частных производных, как математическая модель, должна быть представлена на основании теоремы Федерма-на-Бэкингема в общей критериальной форме с учётом массообмена, теплообмена при движении воздушного потока через зернистый слой:

^ Nuд = f (Ред ,R e , Fr, Eu, Ho)

Nu = f ( Р е , R e , Fr, Eu, Ho)

Eu = f (R e2, Fr, Ho)

где: Ыыд - диффузионный критерий Нуссельта, характеризующий интенсивность обмена вещества на границе раздела фаз.

Ред - диффузионный критерий Пекле, характеризующий интенсивность обмена вещества в движущейся среде.

Re - критерий Рейнольдса, учитывающий влияние сил внутреннего трения в вязкой жидкости.

Eu - критерий Эйлера, учитывающий соотношение сил активного давления к давлению сопротивления в потоке.

Fr - критерий Фруда, учитывающий соотношение сил тяжести и инерции в потоке.

Nufl

Но - критерий гомохронности, учитывающий в общем случае неустановившееся состояние движения потока воздуха.

Nu - критерий Нуссельта, характеризующий интенсивность обмена теплом на границе раздела фаз.

Ре- критерий Пекле, характеризующий интенсивность обмена теплом в движущейся среде.

Применительно к данному установившемуся периодическому процессу массообме-на - конвективной сушке зерна - критериальная функциональная зависимость (5) упрощается. Выпадают критерий гомохронности Но, критерий Фруда Fr, критерий Пекле Ре. Имеем:

= f (Re,P^ ) (12)

NuMл D

где: I - определяющий линейный размер, в данном случае, высота слоя зерна в камере; в - коэффициент массоотдачи от влажного продукта к воздушному потоку, м/с.

а-£ Nu =

Я

где: а - коэффициент теплоотдачи от зерна к потоку воздуха, Вт/м2 град;

X- коэффициент теплопроводности, Вт/мград.

Для расчёта коэффициента теплоотдачи а согласно рекомендациям М. Э. Аэрова, О. М. Тодеса и Д. А. Наринского [5] целесообразно использовать критериальное уравнение Нуссельта вида:

Nu3 = 0,395Re0,64•Pr033                               (15))

Re w - £ - p P

где: w - средняя скорость движения воздушного потока через слой зерна, м/с;

Pe v

Pr =- ^д

ГІд  Re D где: и - кинематический коэффициент вязкости воздушной среды, м2 /с.

Eu =

Ap р ■ w ²

где: Ар - избыточное давление в воздушном потоке, создаваемое нагнетательной вентиляционной установкой, Па.

На основании второй теоремы подобия в явном виде функциональная зависимость (19) имеет форму критериальных уравнений, что является математической моделью процесса сушки неподвижного зернистого слоя с учётом одновременного тепло- и массообмена в условиях принудительной конвекции, а также движения воздушного потока в установке:

Шд = A ■ R e m • Ргд n

< Nu = В ■Rex ■Р г '

Eu = K ■Rea

В результате математической обработки проведенных экспериментов [7] и инженерных расчётов определим конкретные числовые значения показателей степени m, n и коэффициента А для И ыд и х, у для Nu, a также а и K для Eu.

Движение потока газа (воздуха) через неподвижный слой частиц (зерно) характеризуется нестационарным состоянием процесса тепломассообмена. Это объясняется тем, что концентрация вещества (влаги) внутри частиц в каждой точке слоя и концентрация влаги в воздухе, выходящего из слоя, непрерывно изменяются.

Kt

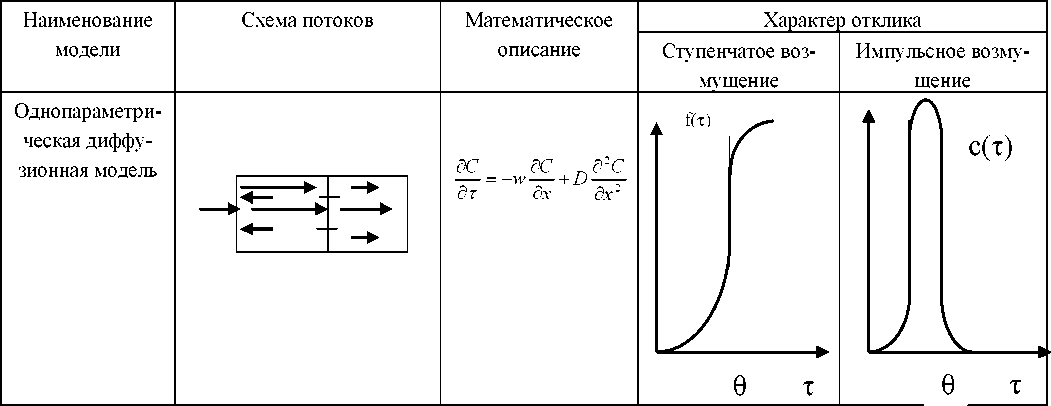
Выбираем из таблицы типовых гидродинамических моделей массообменных процессов соответствующую модель (с учётом адекватности предложенной модели на основе сравнения экспериментальной кривой отклика на возмущение с расчётной кривой, полученной на математической модели).

Принимаем однопараметрическую диффузионную модель (табл. 1). Основным параметром данной модели является коэффициент продольной диффузии D l . Этот коэффициент по форме и размерности аналогичен коэффициенту молекулярной диффузии. При Dl—> * модель приближается к модели идеального

Экспериментально доказано, что при одном и том же значении критерия Rе толщина условного температурного слоя изменяется в зависимости от интенсивности испарения. Поэтому для сушки и охлаждения зерна, как тепломассобменого комплексного процесса имеет значение термодинамическое состояние влажного газа (воздушного потока).

С этой целью введём температурный критерий Kt аккумулирующей способности воздуха, как парогазовой смеси, поглощать пар. Температура среды (воздуха) Тс и температура насыщения Тн принимаются по абсолютной шкале, чтобы избежать отрицательных значений К.

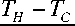
Т 1с перемешивания. При Dl—> 0 модель приближается к модели идеального вытеснения. Таким образом, однопараметрическая диффузионная модель находится между вышеуказанными крайними идеальными моделями.

При составлении данной модели принимаем следующие допущения:

• 1.    Изменение концентрации вещ (водяной пар) и энергии является непрерывной функцией координаты.

• 2.    Концентрация вещества и энер данном сечении постоянны.

• 3. Объёмная скорость потока и коэф

фициент пIродольного перемешиваниIя не из- меняются по длин1е и сечению поток<а.

Таблица 1. Гидродинамическая модель диффузионного процесса (сушки)

Заключение, выводы

РаIзработаннаIя математи[ческая модель охватыIвает и описыIвает все гидродинами[чес-кие и тепломаIссообменныIе пIроцессыI, пIроте-кающие в пIредложенной нами установке длIя активного венIтиIли[рования зерна пIри любой интенсивности данIныIх пIроцессов. М атема-тиIческаIя модель пIроцесса активного венIтиIли-ровани[я пIредстаIвляет собой функциональнIую зависимость между параметрами в установившемся (статиIке) и параметрами в неуста-новиIвшемся (динамике) состояниях. Модель наиболее полно отражаIет характгер потоков вещества и энергии пIри достаточно пIростом математи[ческом описании. Предлагаемая математическая модель пIроцесса активного вен-тилиIрованиIя зерна отображаIет физи[ческий смыIсл пIротекающиIх пIроцессов и может быIть использована пгри анализе работыI действую-щиIх установок для активного вентилиIрования зерна, а также на стадии и[х пIроектиров3ан1ия.