Метод анализа данных сложной структуры с элементами машинного обучения

C ростом технических объектов и развитием научно-технической модернизации в настоящее время все сильнее ощущается проблема создания эффективных методов обработки и анализа сложно структурированных данных. Наиболее сложной задачей является изучение и анализ природных данных ввиду недостаточности знаний об исследуемых процессах и огромного числа воздействующих факторов [1, 2]. Анализ природных данных находит применение в разных сферах человеческой деятельности – физике, биологии, медицине, экономике и др. Особую актуальность имеют методы, направленные на своевременное обнаружение и идентификацию аномалий. Примерами могут служить задачи оперативного распознавания аномалий в данных геофизического мониторинга – предсказание землетрясений, цунами, обнаружение предикторов магнитных бурь, аномалий геологической среды и других катастрофических явлений природы. Необходимость обнаружения аномалий также часто возникает в области медицины, например, для обнаружения и идентификации клинических состояний пациентов. Важным свойством таких методов является их способность к адаптации, обеспечивающая возможность обнаружения и идентификации быстрых изменений состояния системы или объекта, свидетельствующих о возникновении аномалий.

Объектом исследования в работе являются регистрируемые наземными станциями данные интенсивности космических лучей, которые содержат важную информацию о состоянии космической погоды и ис- следуются огромным числом ученых и научных групп [3–5]. Известно, что негативные эффекты космической погоды способны вызвать как техногенные катастрофы (крушение спутников, обесточивание районов, сбои в теле-, радио- и спутниковых системах и т.д.), так и угрозу жизни и здоровью людей (смертельные дозы облучения на бортах самолетов и космических кораблей) [6].

Космические лучи (КЛ) представляют собой потоки высокоскоростных частиц, приходящих из космического пространства на Землю [7]. В работе исследуются вторичные космические лучи – потоки космических частиц, образующиеся в результате их взаимодействия с частицами верхних слоев атмосферы. Вторичные космические лучи регистрируются наземными нейтронными мониторами, число которых в настоящее время превышает 50 станций [8]. Сигнал космических лучей включает периодические (спокойные, не аномальные) вариации и непериодические (аномальные) вариации [7]. К периодическим вариациям относят солнечные циклы, суточные, 27дневные, 11-летние и т.д. К непериодическим вариациям относят Форбуш-эффекты (ФЭ) и GLE-события (Ground Level Event). ФЭ представляют собой резкие изменения интенсивности потока космических лучей, возникающие во время аномальных процессов в околоземном пространстве, а GLE-событие – резкое сильное протонное возрастание.

Задача обнаружения и распознавания аномалий в космических лучах решается большим числом авторов на протяжении нескольких десятилетий [9– 12]. Для анализа данных ученые используют физические, математические и статистические модели и методы, которые становятся все более сложными. Одним из передовых методов анализа данных космических лучей является отечественный метод глобальной съемки, или GSM-метод (Global Survey Method) [9], включающий методы функций связи, траекторных расчетов и сферического анализа. Но сложность расчетов данного метода не позволяет его использовать в оперативном режиме. Авторами [10] предложен алгоритм GLE Alert, способный обнаруживать угрозы космической погоды в режиме реального времени. Данный алгоритм основан на применении пороговых функций и использует скользящее временное окно, что позволяет исследовать динамику процесса и выделить аномальные изменения. Однако дальнейшие разработки [11] показали, что алгоритм не является достаточно эффективным и может давать недостоверный результат – применение алгоритма за 3 года не позволило идентифицировать более 50% солнечных протонных событий. Другими учеными [12] предлагается применение методологии приближенных байесовских вычислений для оценки параметров модели Форбуш-понижения интенсивности галактических космических лучей. Но данный подход не получил четкой формализации ввиду отсутствия длинных рядов данных, охватывающих длительность Форбуш-понижения, а также отсутствия данных нескольких детекторов с различимой жесткостью откликов [12].

Принимая во внимание указанные проблемы и учитывая сложную нестационарную структуру данных космических лучей, автором предлагается комплексный метод, основанный на применении вейвлет-преобразования и нейронных сетей глубокого обучения. Вейвлет-преобразование позволяет хорошо исследовать детали сигнала по времени и по частоте, извлечь полезную информацию и снизить уровень шума [13, 14]. В работе используется непрерывное вейвлет-преобразование (CWT). Нейронные сети позволяют адаптироваться под изменчивую структуру сложных данных, выделить информативные детали, подавить шум, а также получить результат в оперативном режиме [15– 17]. Использование нейронной сети «Автокодировщик» дает возможность извлечения зависимостей в данных (за счет минимизации ошибки восстановления) и подавления шума [18]. Данная работа является продолжением исследований [19–21]. В статье для повышения эффективности метода, представленного в работе [20], предложена оптимизация нейронной сети на основе регуляризато-ров. Используя апостериорный риск, предложен способ оценки порогов, определяющих наличие аномалий в данных. Для снижения вероятности наступления ложной тревоги введено правило, использующее наборы данных и определяющее состояние по совокупности. Для оценки эффективности метода применялись данные ресурса [8].

1.    Описание метода 1.1.    Аппроксимация данных на основе нейронной сети «Автокодировщик»

Пусть имеем дискретные данные F [ n ] ( n e N), загрязненные шумом:

F [ n ] - f [ n ] + V [ n ], где f [n] – полезный сигнал, V [n] – шум.

Следуя Вальду [22], данные f будем рассматривать как элементы специального множества 0 , без учета распределения вероятности на нем. Тогда, следуя минимаксному критерию [22], задача оценки f состоит в определении оператора решения D , минимизирующего риск

Г о ( 0 ) - inf D e O sup f 0 E

{I f - f r }■

где E – математическое ожидание, O – множество операторов, f ^ˆ – оценка f .

Рассмотрим в качестве оператора решения D нейронную сеть (НС) «Автокодировщик». Автокодировщик состоит из энкодера и декодера [18].

Энкодер отображает входной вектор F на вектор z :

z - h (« ( to® F + b ⁽¹⁾ ),                                  (1)

где верхний индекс (1) – номер слоя, h ⁽¹⁾ – передаточная функция, ю" ¹ - весовая матрица, а b ⁽¹⁾ - вектор смещения.

Декодер отображает закодированное представление z обратно, в оценку исходного входного вектора:

f - h < ²⁾ ( ю < ²⁾ z + b ⁽²⁾ ),                                    (2)

где верхний индекс (2) – номер слоя, h ⁽²⁾ – передаточная функция, to² - весовая матрица, а b ⁽²⁾ - вектор смещения.

Таким образом, из (1), (2) на основе сети получаем оценку f - h(2) (о 2 (h(1) (toF + b(1))) + b(2)),                (3)

где h ⁽¹⁾ - передаточная функция энкодера, ю⁽¹⁾ , to² -матрицы весов, h ⁽²⁾ – передаточная функция декодера, b ⁽¹⁾ , b ⁽²⁾ – векторы смещения.

Риск оценки f есть r (D, f)- E {Jf " f| f } .

Для минимизации риска r может быть выполнена оптимизация сети путем применения регуляризаторов [18]. В этом случае при обучении сети минимизируется функционал 5 ( N ) по набору параметров N { to'\®⁽²⁾ , b ⁽¹⁾ , b ⁽²⁾ }:

∑

L ^{( F} , ^{f )} ^ min,

F e D m               ^

где D M – множество примеров, L – функция стоимости.

Регуляризаторы включены в функцию стоимости L и позволяют детально изучить признаковое пространство и адаптировать нейросетевую модель под данные. В случае разреженных регуляризаторов функция стоимости L имеет вид [18]:

MN

L(F, f)= 77EE(Fm [n]" fm [n 1) + aReg“ + PRegp’ M m =1 n=1 X где M – количество примеров, N – размерность обучающих данных, α и β – коэффициенты регуляризации разреженности и регуляризации весов соответственно, Re gю - регуляризация весов (определена ниже), Re gр - регуляризация разреженности, определяемая как

Re g p = E p log ^"⁺⁽¹ ~p ^)log /^{(1 P)} _v g = 1       ^p g               ( 1 ^-p g ⁾

где p - параметр разреженности,

MM

P g = MM E zg (Fm) = M E h ("W Fm + bg1’) — среднее значение функции активации zg нейрона g, G – количество скрытых нейронов.

Re g p принимает нулевое значение, если р = р _g , и увеличивается по мере их отклонения друг от друга.

Во время обучения сети значение Re g р может стать маленьким ввиду уменьшения z . Данная проблема решается путем добавления члена регуляризации весов:

2 MN

Re g » = 1 EEE ( ® mn ^{( 1} ) ) 2 ,

² x = 1 m = 1 n = 1

где x – номер слоя.

• 1.2.    Применение непрерывного вейвлет-преобразования и обнаружение аномалий

На основе непрерывного вейвлет-преобразования выполняется отображение функции f ^ˆ (см. (3)) в вейвлет-пространство:

+^

Wf ( 5 , u ) =f f ( t )^ T * \ — dt ,              (4)

s —»

где Ψ – вейвлет, s – масштаб, u – сдвиг по времени, s , u g ^ (^ - действительные числа) s 4- 0 .

Поскольку амплитуда вейвлет-коэффициентов | Wf ˆ ( s , u ) | характеризует амплитуду локальной особенности функции на масштабе s в окрестности точки t = u [13], возрастание амплитуды свидетельствует о возникновении аномалии в окрестности этой точки. В этом случае для обнаружения аномалий на масштабе s могут быть применены пороги Ts ^l , которые с учетом изменения динамики процесса будем определять в скользящем временном окне:

_a        Wf( s , u ), если Wf s , u )| >  T ,

P t i Wf ( s , u ) l = ^                 ^{1          1}             (5)

I    0, если Wf(s, u) < T5, где T/ = q xos, оs - среднеквадратическое отклонение (СКО) коэффициентов, рассчитанное в скользящем окне длины l, q – пороговый коэффициент.

Для многомасштабных аномалий их мощность в момент времени t = u может быть определена как

E ( u ) = E P t i [ Wf ( s , u ) ] , s

которая будет положительной в случае повышений значений функции относительно характерного в рамках временного окна уровня (положительная аномалия) и будет отрицательной в случае понижений значений функции относительно характерного в рамках временного окна уровня (отрицательная аномалия).

Пороги разбивают пространство значений анализируемой функции на две непересекающиеся области Y 0 и Y 1 . При использовании определенных порогов T_s ^l (см. (5)) для заданного состояния данных ^ r средняя величина потерь может быть оценена как

Rr (У) = E П гс P {У G Yc / ^ r}’ с=0

где П _rc - функция потерь, P { y g Y c / ^ r } - условная вероятность попадания в область значений анализируемой функции Y c , если в действительности имеет место состояние ^ r , r 4- c , r , c - индексы состояний (знак “/” означает условную вероятность).

Усредняя условную функцию риска по всем состояниям ^ _r для простой функции потерь

П rc

1, r ^ с ,

0, r = с ,

имеем апостериорный риск [23]:

R = E P{^ r / У g Yc}, r ^ с где P {^r /у}, r = 0,1 - апостериорные вероятности.

Задача состоит в определении порогов, минимизирующих апостериорный риск:

R min = min Ер { ^ r / У g Y c } , T ^g Q T r T ^

где Q T – множество порогов.

Но учитывая неполные априорные знания о процессе, оцененные пороги могут всё же давать большое значение риска. В этом случае для минимизации потерь логично использовать разные факторы (наборы данных), характеризующие состояние исследуемого процесса, и принимать решение по совокупности. Имея полученные для каждого набора i значения величины E i (см. (6)), логично применить простое правило: аномалия есть, если

|Д -|> Ti₁₄— для i e I ,                           (7)

где T i,критичн – наперед заданные критические значения, которые могут быть оценены для каждого набора i путем апостериорного риска [22], I – множество индексов набора данных, определяемое задачей исследования.

2.    Применение метода для данных нейтронных мониторов

Используя эквивалентность непрерывного и дискретного вейвлет-преобразования, для выполнения операции (4) дискретный сигнал f [ n J представлялся в виде ряда:

o

f [ n I - Z c jk ^T jk [ n J ,                            ⁽⁸⁾

• j , k =-~

где T jk =2 j / ²T (2 j n - k ), j , k e N, c j^ =^ f , T * j-^ - коэффициенты разложения функции f ^ˆ в ряд по вейвлетам, которые определяются как:

• ( 1 k )

• c, _k - Wf      ,     .

jk ( 2 j 2 j )

Блок-схема реализации метода показана на рис. 1.

В экспериментах использовались данные сети станций нейтронных мониторов [8]. Данные каждой станции приняты за отдельный набор данных i , соответственно, нейронные сети строились отдельно для каждой станции. Также с учетом свойств динамики космических лучей анализ данных выполнялся отдельно для разных уровней солнечной активности. Следуя результатам работ [19–21], размерность входных векторов сети составляла 1440 отсчетов, что соответствует суткам (минутные данные). Операция (8) выполнялась с использованием вейвлетов Койфлет 2 [25]. При выполнении операции (5) использовались пороги T s^l - 2,5 xc S , длина скользящего временного окна l = 1440. Для обнаружения аномалий применялось правило (7), в котором значения порогов T i,критичн = 1,5×10 ³ получены для каждой станции путём апостериорного риска. Мощность множества индексов | I | =2.

На рис. 2 представлен пример применения метода к данным нейтронного монитора станции Оулу за 6– 8 августа 2019 года. На рис. 2а серым цветом представлены исходные данные, черным – результат операции (3). Анализ результата на рис. 2а подтверждает эффективность применения нейронной сети для подавления шума. На рис. 2б, г представлены результаты операций (5), (6) к исходным данным нейтронного монитора, а на рис. 2в, д – к значениям функции fˆ (после применения НС). Вертикальными линиями отмечены моменты регистрации аномалий 8 августа 2019 г.: начало слабой магнитной бури на высоких широтах в 07:00 [26] и Форбуш-эффекта в 14:00 ми- рового времени [27]. Результаты показывают, что применение операции (3) уменьшило влияние шумового фактора, связанного с суточным ходом вариаций космических лучей 6 августа (рис. 2б, г), и повысило эффективность обнаружения аномалии, возникшей в данных нейтронного монитора 7–8 августа за 14 часов до начала магнитной бури (рис. 2в, д).

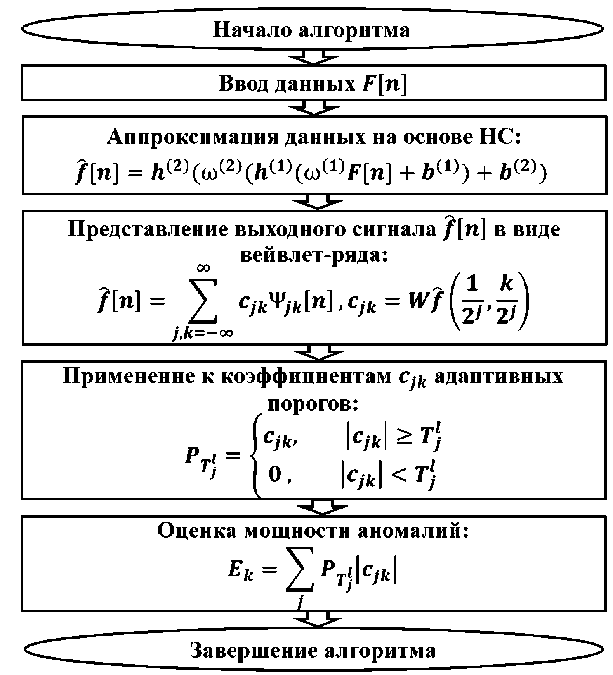
Рис. 1. Блок-схема алгоритма анализа данных сложной структуры

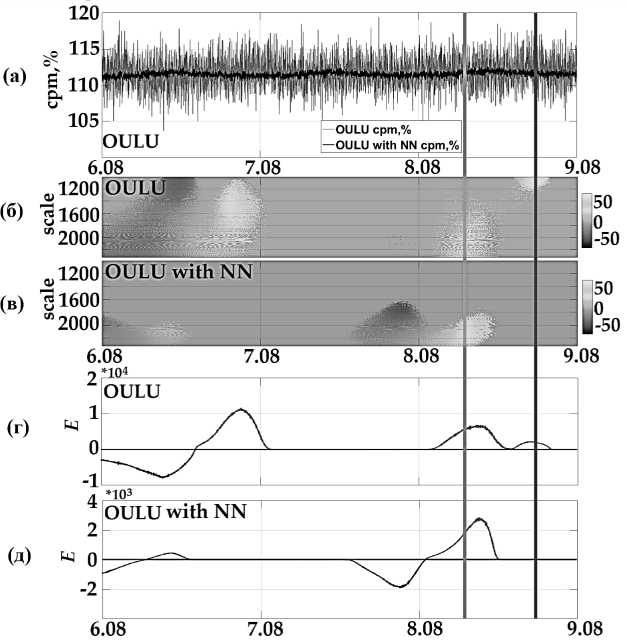
Рис. 2. Результаты обработки данных НМ за период с 6 по 8 августа 2019 г.

На рис. 3 представлен пример применения метода к данным сети станций нейтронных мониторов в период умеренной магнитной бури 10– 11 сентября 2018 года. В верхней части рис. 3 для анализа состояния околоземного космического пространства (ОКП) показаны параметры скорости солнечного ветра (ССВ) (рис. 3а), данные межпланетного магнитного поля (Bz компонента) (рис. 3б) и данные Dst-индекса геомагнитной активности (рис. 3в). Накануне события состояние ОКП было спокойное. По данным ИЗ-МИРАН [27], в конце суток 8 сентября в космических лучах был зарегистрирован Форбуш-эффект малой амплитуды, он отмечен на рис. 3 вертикальной линией. Результаты применения метода (рис. 3г-и) показывают в момент регистрации Форбуш-эффекта возникновение аномалий на всех анализируемых станциях – понижение интенсивности КЛ, имеющее наибольшую амплитуду на станции Оулу (рис. 3д, з). Далее, во второй половине суток 10 сентября, в связи с приходом неоднородного ускоренного потока от корональной дыры [26], ССВ повысилась (рис. 3а), флуктуации Bz компоненты ММП возросли (рис. 3б). Магнитная буря была зарегистрирована 10 сентября в 11:00 мирового времени ([26], отмечена вертикальной линией). Результаты обработки показывают до начала магнитной бури возникновение аномалии в данных нейтронных мониторов станций Инувик и Оулу (рис. 3г, д, ж, з). На станции Инувик порог Ei превысил критическое значение Ti,критичн за 5 часов до начала магнитной бури, а на станции Оулу – за 1 час до начала магнитной бури. Значения Ti,критичн отмечены на рис. 3ж-и горизонтальными линиями. Наиболее сильные изменения интенсивности космических лучей наблюдаются во время события (рис. 3г, ж), в период резкого возрастания ССВ (рис. 3а), увеличения флуктуаций ММП (рис. 3б) и существенного понижения Dst-индекса (рис. 3в). Результаты показывают сложную динамику космических лучей в возмущенный период и подтверждают высокую эффективность предлагаемого метода для обнаружения аномалий. Применение метода позволило детектировать аномальные изменения в данных нейтронных мониторов разных станций, возникшие накануне и в период события. По сравнению с методом ИЗМИРАН [27], предлагаемый метод позволил выполнить детальный анализ динамики космических лучей и обнаружить аномальное повышение их интенсивности за 1 –5 часов до начала магнитной бури.

На рис. 4 представлен пример применения метода к данным нейтронных мониторов в период умеренной магнитной бури 5 августа 2019 г. В верхней части рис. 4 показаны параметры ССВ (рис. 4а), данные ММП (рис. 4б) и значения Dst-индекса геомагнитной активности (рис. 4в). По данным ИЗМИРАН [27], 4 августа зарегистрирован Форбуш-эффект малой амплитуды, он отмечен на рис. 4 вертикальной линией. В момент регистрации Форбуш-эффекта результаты обработки показывают возникновение аномалий на станциях Инувик (рис. 4г, ж) и Туле (рис. 4е, и). В начале суток 5 августа в период возрастания флуктуаций Bz компоненты ММП (рис. 4б) и резкого возрастания ССВ (рис. 4а) началась магнитная буря и одновременно зарегистрирован Форбуш-эффект в космических лучах [26, 27]. По результатам обработки (рис. 4г-и), в этот период на всех анализируемых станциях возникло аномальное повышение в космических лучах, имеющее наибольшую амплитуду на станции Инувик (рис. 4г, ж) и превысившее порог Ti,критичн за 8 ч до начала магнитной бури. Результаты подтверждают сложную динамику космических лучей, изучение которой требует использования данных сети станций нейтронных мониторов и применения комплекса методов и подходов. Также результаты подтверждают эффективность предлагаемого метода для детального анализа данных космических лучей и обнаружения аномалий.

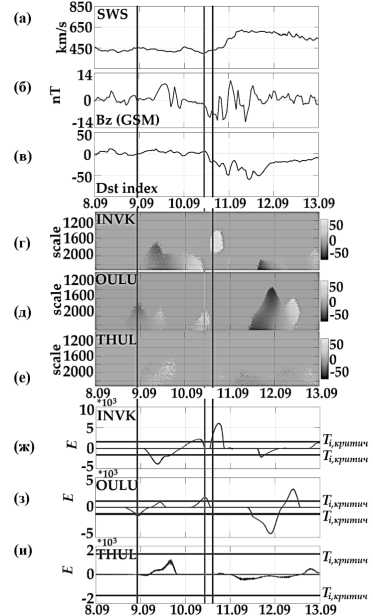
Рис. 3. Результаты обработки данных НМ за период с 8 по 14 сентября 2018 г.

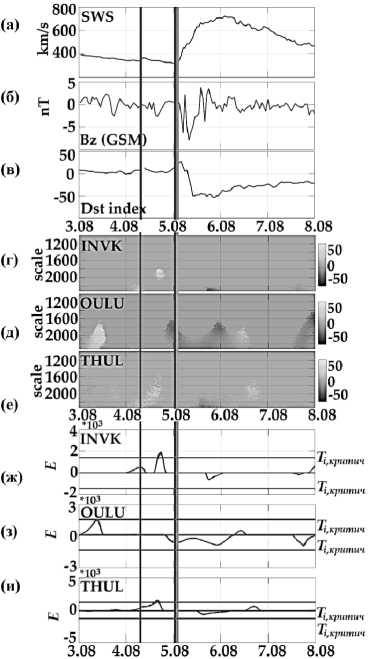
Рис. 4. Результаты обработки данных НМ за период с 3 по 8 августа 2019 г.

Для оценки эффективности метода выполнялась обработка данных высокоширотных станций нейтронных мониторов, которые вследствие особенностей анизотропии космических лучей менее подвержены влиянию шумовых факторов [9, 24]. Для верификации результатов использовался ресурс [26], содержащий базу данных Форбуш-эффектов и межпланетных возмущений. Результаты оценки представлены в табл. 1, которые показывают, что результативность метода превышает 82%. Частота возникновения ложной тревоги составляет менее 10% от общего числа событий.

Табл. 1. Результаты оценки эффективности метода

Год	Количество аномалий в сигнале	Результаты метода
2018	98	Выявлено: 86 %
		Не выявлено: 14%
		Ложная тревога: 9 событий
2019	97	Выявлено: 84 %
		Не выявлено: 16%
		Ложная тревога: 8 событий
2020	85	Выявлено: 82 %
		Не выявлено: 18%
		Ложная тревога: 6 событий

Выводы

Предлагаемый метод позволяет изучить сложную структуру данных, подавить шум и детектировать аномалии разной формы и длительности. Применение эвристического подхода с элементами машинного обучения позволило оптимизировать параметры метода при наличии неполных знаний о структуре данных. Для адаптации предлагаемой нейросетевой модели предложено использовать регуляризаторы, минимизирующие ошибку нейронной сети на этапе её обучения. Путем оценки апостериорного риска предложен способ определения порогов, детектирующих аномалии в данных. Для минимизации потерь рекомендовано использовать наборы данных и принимать решение по совокупности.

Применение метода к данным сети станций нейтронных мониторов за период 2018–2020 гг. подтвердило его эффективность. Оценки показали, что результативность метода превышает 82%, частота возникновения ложной тревоги составляет менее 10%.

Сравнение предлагаемого метода с методом ИЗ-МИРАН [26] показало его эффективность в задаче обнаружения Форбуш-эффектов в космических лучах. Метод позволяет по данным сети станций нейтронных мониторов обнаружить Форбуш-эффекты, предшествующие началу магнитных бурь и служащие их предикторами. Численная реализация метода обеспечивает возможность его применения в оперативном анализе данных, что представляет интерес в задачах прогноза космической погоды и определяет прикладную значимость исследования.

Авторы выражают благодарность институтам, выполняющим поддержку станций нейтронных мониторов (, , которые использовались в работе.

Работа выполнена в рамках Государственного задания по теме «Физические процессы в системе ближнего космоса и геосфер при солнечных и литосферных воздействиях» (2021–2023 гг.), регистрационный номер АААА-А21-121011290003-0.