Методические особенности использования современных информационных технологий в преподавании физики в высшей школе

ля со студентами. Происходит изменение характера педагогической деятельности, выстраивается новая образовательная модель.

Применение ИКТ в образовательной среде позволяет готовить специалистов, не только обладающих запасом глубоких научных знаний и профессиональных компетенций, но и владеющих определенными навыками в области информационных технологий. Использование разнообразных математических пакетов при подготовке специалистов естественно-научного направления повышает эффективность и вариативность обучения, активизирует учебный процесс.

Ряд математических пакетов существенно расширяет класс математических моделей, допускающих глубокий детальный анализ и проведение вычислительного эксперимента без трудоемкого написания программ на языках программирования. Среди них весьма распространенными являются такие, как Maple, Mathematica, MathCAD, MatLab и Maxima. Эти системы обладают широкими возможностями, позволяющими выполнять вычисления в символьном и численном виде, операции с векторами и матрицами, решать системы алгебраических и дифференциальных уравнений, обладают большими графическими возможностями и т. д. [1]. Применение систем компьютерной математики значительно упрощает решение задач по классической механике, теоретической физике, электрорадиотехнике и позволяет визуализировать полученные результаты.

Hовейшие информационные технологии вытесняют традиционные формы обучения, заменяя их более технологичными и динамичными методами обучения. Современные технологии позволили перейти к дистанционному обучению, получившему интенсивное развитие в образовательном процессе. Проведение интерактивных занятий (видеоконференций, виртуальных лабораторных работ, тестирование и т. д.) позволяет совершенствовать педагогическую деятельность в инновационном образовательном процессе.

Исследование динамики консервативной механической системы. Для дисциплины «Теоретическая физика», входящей в раздел «Классическая механика», нами разработан комплекс индивидуальных заданий для студентов на исследование динамики механических систем со многими степенями свободы. Цель заданий – отработка навыков применения методов математической физики в сочетании аналитического расчета с компьютерным моделированием физических процессов и ис- пользованием современных математических пакетов. Учитывая степень подготовки и уровень владения навыками работы студентов с математическими пакетами, на начальном этапе им предлагается повторить основные принципы работы в выбранной среде компьютерной математики [2; 3], разобраться в решении типовой физической задачи и выполнить задание оригинальное.

Рассмотрим использование математических пакетов для решения задач механики на исследование колебаний консервативной механической системы с двумя степенями свободы. Поскольку уравнения Лагранжа дают единый (и при этом достаточно простой) метод решения задач динамики, используем формализм Лагранжа. Отметим основные преимущества его уравнений: a) вид и число уравнений не зависят от количества тел, входящих в рассматриваемую систему; б) независимость от траекторий движения тел; в) число уравнений Лагранжа определяется только числом степеней свободы; г) при идеальных связях эти уравнения позволяют исключить из рассмотрения все неизвестные реакции связей [4].

Проанализируем задачу на исследование динамики плоского маятника. Материальная точка массой m (муфта) может без трения двигаться вдоль невесомого стержня, закрепленного в точке подвеса (рис. 1.). Муфта соединена пружиной жесткостью k с точкой подвеса. Длина недеформированной пружины l ₀. Нужно найти функцию Лагранжа такого плоского маятника, находящегося в однородном поле тяжести (g – ускорение свободного падения), аналитически получить функцию Лагранжа, составить уравнения Лагранжа и численно исследовать динамику такой механической системы при различных параметрах. Численное исследование динамики и компьютерное моделирование механической системы рекомендуется провести в одном из современных математических пакетов – Maxima или Maple.

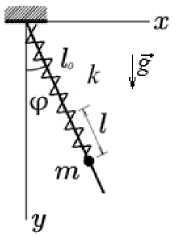
Рис. 1. Геометрия задачи

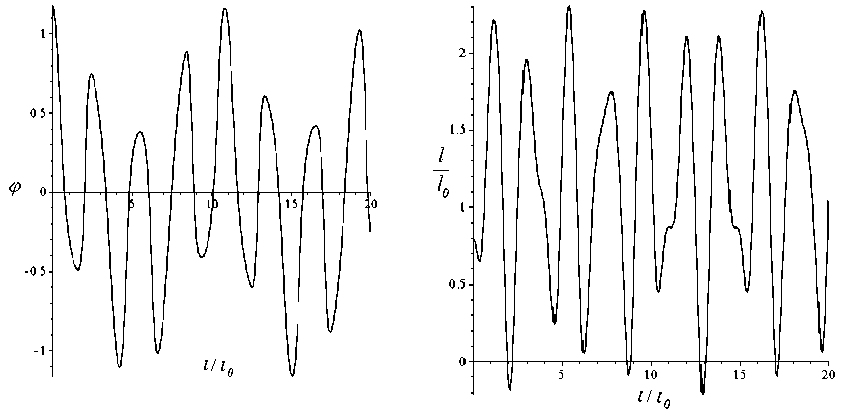
Рис. 2. Графики зависимости ^(t) и l(t)

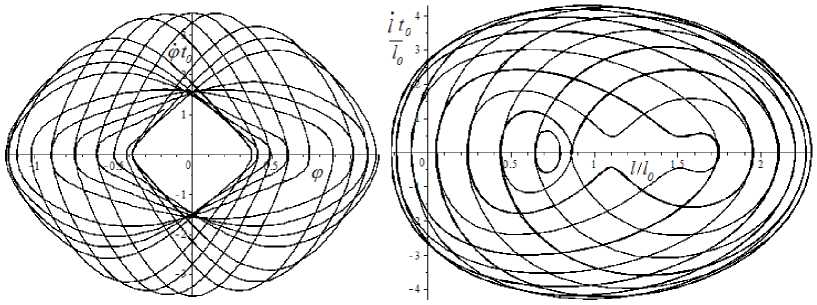
Рис. 3. Фазовые портреты ф ( ф ) и / ( l )

Используем формализм Лагранжа, т. к. уравнения Лагранжа представляют собой эффективный инструмент для решения задач теоретической механики и дают единый и при этом достаточно простой метод решения задач динамики [4].

Как и при решении любой физической задачи, для исследования динамики консервативной системы студентам предлагается пользоваться стандартным алгоритмом.

• 1.    Изобразить систему в произвольном положении. Определить число степеней свободы рассматриваемой механической системы.

• 2.    Указать все действующие активные силы и выяснить, являются ли они потенциальными.

• 3.    Определить кинетическую энергию системы в обобщенных координатах и скоростях.

• 4.    Определить потенциальную энергию системы в обобщенных координатах.

• 5.    Составить функцию Лагранжа и уравнения Лагранжа второго рода.

• 6.    Решить уравнения относительно искомых параметров аналитически (если это возможно). Проверить предельные переходы к известным результатам.

• 7.    Подготовить систему дифференциальных уравнений второго порядка к численному расчету, выполнив обезразмеривание и переход к системе уравнений первого порядка.

• 8.    Построить графики зависимости обобщенных координат от времени и фазовые портреты.

• 9.    Проверить выполнение закона сохранения энергии для рассматриваемой системы.

• 10.    Построить компьютерную модель механической системы.

• 11.    Провести компьютерный эксперимент и проанализировать полученные результаты моделирования при вариации модельных параметров. Сравнить результаты эксперимента с аналитическим решением в ряде предельных случаев.

Функция Лагранжа для данной задачи имеет вид ь^-и^ф +(/0 + /)V) + к!1

+ mg(l₀ + /) cos ф —— ^.

Уравнения Лагранжа для каждой обобщенной координаты φ и l образуют систему дифференциальных уравнений второго порядка

(/₀ + Гур + 21 ф + g sin ф = О ;

ml - тЦ_й + Пф² — mg cos ф + kl = О.

После перехода от системы уравнений (2) к системе уравнений первого порядка и численных исследований динамики плоского маятника в среде Maple можно получить графики зависимости обобщенных координат от времени φ ( t ), l ( t ) и фазовые портреты ϕ & ( ϕ ) и l ^& ( l ) .

Результаты численного исследования приведены на рис. 2 и 3 для случая mg / k = 0,98 и начальных значений параметров l/l₀ = 0,8, φ = 3 π /8.

В частном случае, когда начальное значение φ = 0, рассматриваемая система представляет собой пружинный маятник, совершающий гармонические колебания по закону l = mg/k + lнcos(ωt+φн) с частотой ω2 = k/m. Этот случай позволяет убедиться в правильности построения модели, сравнив результаты численного расчета с аналитическим решением.

Приведем еще один пример решения задачи на исследование динамики плоского маятника. Точка массой m ₂ может двигаться только по вертикальной оси y (рис. 4). К ней пружинкой прикреплен маятник длиной a и массой m₁ . Характеристики пружинки: жесткость k и длина в недеформированном состоянии l ₀. Пружинка не провисает в процессе движения (через нее проходит длинный невесомый стержень, который может легко поворачиваться в точке массой m₂ и свободно проходить через точку m₁ ). Необходимо найти функцию Лагранжа такого плоского маятника, находящегося в однородном поле тяжести, составить уравнение Лагранжа и численно исследовать движение такой механической системы. Трением в данном случае можно пренебречь.

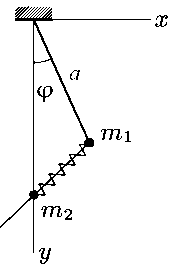
Рис. 4. Геометрия задачи

Функция Лагранжа для данной задачи имеет вид

. т.сгф2 т3у; ,                х

L = —+ gU^a cos ф + т_гу_г) -

- к^а¹ + v² -2y₂acos^ -1_оУ

.

Уравнения Лагранжа для каждой обобщенной координаты φ и y2 образуют систему дифференциальных уравнений второго порядка ip + — sin ф + ——sin ^7(1 —,     ^°      =) = О а тх «        ^а2 + у2 -2у,асо§ф к                                 I

У2 - g + — (у2 - ^{а cos} ^)(! - / ,    , °          ) = ⁰

т2               -^а" + у;-2у2асо§ф

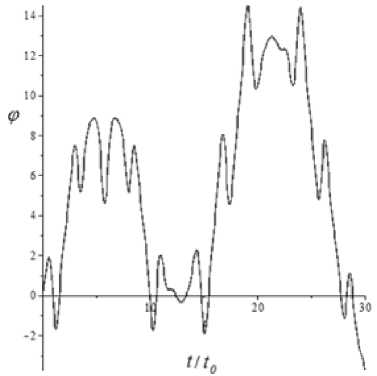
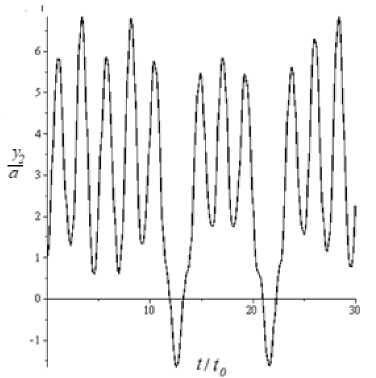
Рис. 5. Графики зависимости φ ( t ) и y₂ ( t )

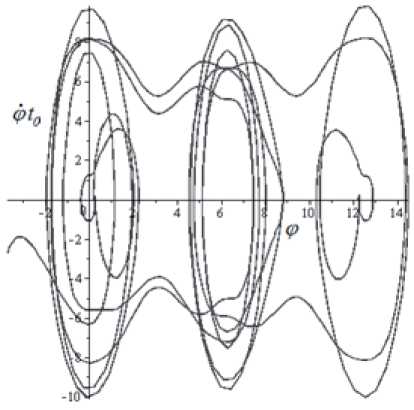
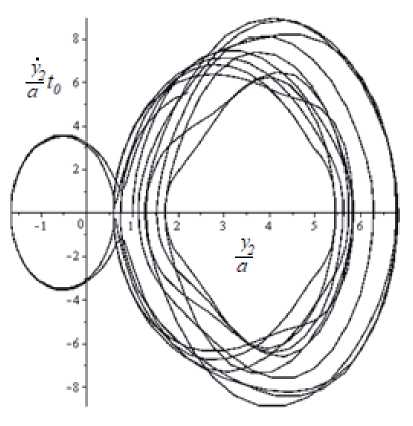
Рис. 6. Фазовые портреты ϕ & ( ϕ ) и y & ( l )

После перехода от системы уравнений (5) к системе уравнений первого порядка и численных исследований динамики плоского маятника в среде Maple можно получить графики зависимости обобщенных координат от времени φ ( t ), y₂ ( t ) и фазовые портреты ϕ & ( ϕ ) и y & ₂ ( l ) .

Результаты численного исследования приведены на рис. 5 и 6 для случая m₁ = m₂ и начальных значений параметров l₀/a = 2,5, y₂/a = 1,0, φ = 0,2 , ϕ & = 0 .

Образцы решения нескольких разноплановых задач позволяют преодолеть начальный барьер вхождения в проблему, использовать алгоритмы и шаблоны для последующего решения уже оригинальных задач. Такой подход позволяет одновременно освоить методы решения теоретических задач и, используя математические пакеты, визуализировать решение, освоить методы компьютерного моделирования. Все вышесказанное является основой для продуктивной учебно-педагогической и научно-исследовательской деятельности студентов. Подбор тематики исследовательских проблем очень важен, даже простые базовые задачи можно модифицировать, получая интересные результаты. В качестве примера можно привести проблему нахождения вектора напряженности и потенциала поля равномерно заряженной прямой нити из электростатики, доведенную до уровня творческого исследования, в котором студентам необходимо найти нестандартные методы решения с новыми для них математическими объектами [6].

Исследование динамики электрической системы. В электрорадиотехнике использование лагранжева формализма тоже является весьма продуктивным: для анализа цепей, содержащих резисторы, емкости, индуктивности, источники напряжения, исследования систем с распределенными параметрами для анализа передачи и фильтрации электромагнитных волн.

Функция Лагранжа радиотехнической системы представляет собой сумму лагранжианов электрического поля зарядов конденсаторов, магнитного поля токов в проводниках и лагранжиана взаимодействия зарядов и токов с внешним электромагнитным полем. В последнем случае в качестве «кинетической» энергии выступает энергия магнитного поля, а в качестве «потенциальной» – энергия электрического поля, учет потерь на тепло Джоуля – Ленца осуществляется введением обобщенной силы (или диссипативной функции) в уравнения движения. Подход легко обобщается на случай наличия подвижных подсистем (якорь, ротор и т. д.).

Для демонстрации целого ряда опытов по электромагнетизму в школе используется набор «Трансформатор универсальный», который позволяет демонстрировать эффектное явление левитации проводящего кольца при подключении трансформатора к сети переменного тока [7]. Левитация кольца в рассматриваемых опытах обеспечивается силой Ампера, возникающей в результате взаимодействия радиальной составляющей неоднородного магнитного поля с индукционным током, создаваемым переменной осевой составляющей поля электромагнита при наличии индуктивного сопротивления кольца такой величины, чтобы выполнялось условие равновесия. Кольцо может совершать колебания, для этого режима принципиальным является инерция кольца. Эффект можно описать на языке лагранжева формализма. Рассмотрим горизонтально расположенное тонкое кольцо с массой m и площадью S, находящееся во внешнем неоднородном переменном магнитном поле, направленном вдоль оси z с вектором индукции B(t,z) = A0(t)B1(z), где B1(z) заданная функция, а A0(t) = cos(ωt). Функция Лагранжа в этом случае примет вид:

1     ,1 э

, где Λ – индуктивность кольца. Запишем уравнения Лагранжа:

•• СЛ /^dBl(Z)•

, dz

.

at

В уравнения Лагранжа сопротивление и трение были введены посредством обобщенных сил (или диссипативных функций) F R = - R • q , F = - y • z . Второе уравнение можно представ ить в виде

.

dt

В случае преобладания индуктивного сопротивления ток равен q = -SA0(t)B](z)/A. Усредняя первое уравнение Лагранжа по вре- мени, получим уравнение, описывающее медленное движение (частота изменения поля много больше характерной частоты или об- ратного времени релаксации кольца в процессе движения вдоль оси z) кольца

S^d^Jz))^

4Л dz

.

Левитация возможна, в случае dBilz)) < 0 dz на высоте z = Zo, значение которой определяется из уравнения

S2 dCB^z))2 .

.

4A dz

Эффект магнитной левитации, связанный с появлением в «вибрационном» силовом поле медленно меняющейся во времени силы, компенсирующей притяжение, интересен не только с исторической, но и с методической точки зрения. Появление регулярной силы было впервые продемонстрировано на экспериментально реализованном маятнике на вибриру-

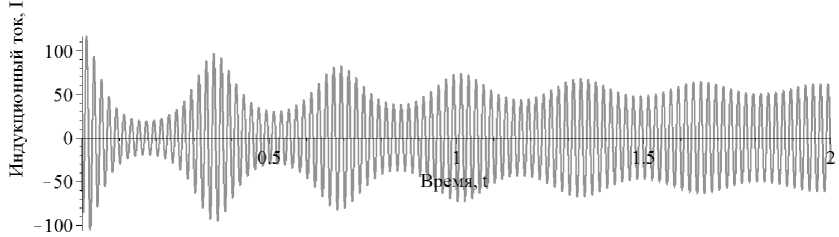
Рис. 7. Временная развертка индукционного тока

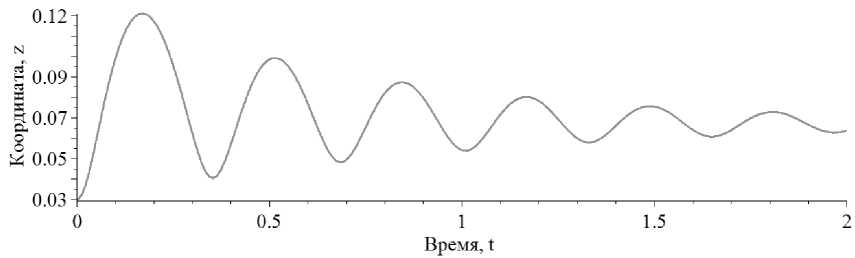
Рис. 8. Зависимость высоты подъема кольца от времени

ющем подвесе (П.Л. Капица) и проанализировано в большом количестве теоретических исследований.

Использование функции Лагранжа применимо и в случае распределенной системы. Рас- смотрим цепочку, состоящую из n звеньев, в каждое из которых входят катушка и конден- сатор, которые соединены последовательно. Каждая следующая ячейка подключается параллельно конденсатору предыдущей ячейки. Цепочка подключена к источнику гармонически изменяющегося напряжения. Функция Ла- гранжа для такой системы имеет вид

L=\.i^ ~^„ -я„У) +

.

Тем студентам, которые проявили интерес к исследованию поставленных задач, предлагается их развить, используя нелинейную динамику, современную теорию колебаний [5]. При выполнении заданий студенты используют виртуальную лабораторию, которая построена на сервере с 8-ядерным процессором Xeon и лицензионной программой Wolfram Mathematica.

Цифровые технологии уже не только активно применяются в научных исследованиях, но и входят в нашу жизнь: «умный дом», автоматическое и дистанционное управление электрическими системами, робототехника. Появление микропроцессорных систем с открытым исходным кодом, основанных на про- стом в использовании аппаратном и программном обеспечении (например, Arduino), привело к их активному использованию в наших лабораториях общей физики и электрорадиотехники.

Созданы измерительные приборы с возможностью накопления данных и передачи их для последующей обработки на компьютере. Они оказались весьма продуктивны для измерения температуры, тока, напряжения, индукции магнитного поля и других физических величин.

На занятиях электротехники и радиотехники студенты помимо готовых лабораторных заданий получают индивидуальные задания на разработку конечных микропроцессорных устройств прикладного характера. Будущие педагоги, осваивая эти технологии, готовятся к работе в школе в новых условиях активизации научно-исследовательской и проектной деятельности учащихся.

Описанные выше типы заданий позволяют студентам получать навыки применения методов теоретической физики и умелого сочетания аналитического расчета с компьютерным моделированием физических процессов и использованием современных математических пакетов. Все вышесказанное активизирует учебно-познавательную деятельность студентов, повышает мотивацию к изучению теоретической физики, формирует информационные и исследовательские компетенции.

Применение сетевых технологий, технологий дистанционного обучения, обеспечивает доступ студентов и преподавателей к информационным ресурсам и средствам получения новых знаний при работе с программными продуктами, размещаемыми на сервере учебного заведения. Они помогают организовывать самостоятельную работу студентов, индивидуализировать и синхронизировать процесс обучения.

В заключение сформулируем основные выводы.

• 1.    Сочетание аналитического расчета с компьютерным моделированием физических процессов с использованием современных математических пакетов позволяет облегчить процесс изучения дисциплин общей и теоретической физики.

• 2.    Использование современных математических пакетов значительно упрощает выполнение и оформление математических исследований как в символьной, так и в численной форме. В частности, позволяет удобно и бы-

• стро выполнять исследование динамики сложных механических систем.

• 3.    Применение математических пакетов позволяет студентам компенсировать недостаток знаний математического аппарата, численных методов и тонкостей программирования на языках высокого уровня, поскольку они содержат обширный набор библиотек для выполнения математических расчетов.

• 4.    Сетевые технологии обеспечивают доступ студентов и преподавателей к информационным ресурсам и средствам получения новых знаний при работе с программными продуктами, размещаемыми на сервере учебного заведения, тем самым приобретают навык удаленной и групповой работы, свойственный современным научным коллективам.

• 5.    Использование открытых микропроцессорных платформ позволяет активизировать научно-исследовательскую и проектную деятельность студентов.