Методические подходы при экспериментальном обучении математике студентов вуза

Развитие методики обучения математике на современном этапе высшего образования характеризуется системными исследованиями образовательного процесса. Для формирования фундаментальных знаний студентов необходимо использовать комплексный подход, в котором гармонично сочетались бы теории, методики и модели обучения математике. В условиях новых образовательных стандартов должны быть разработаны такие учебники, методические пособия и программы, которые позволили бы студентам эффективно усваивать материал по курсу высшей математики на обязательном и углубленном уровнях. Считаем, что это возможно за счет реализации в разрабатываемых курсах различных межпредметных и внутрипредметных связей. Как отмечалось нами ранее1, анализ и усиление внутрипредметных связей необходимо учитывать в качестве важного направления дидактического совершенствования курса математики.

Из-за разного восприятия студентов в учебном процессе целесообразно использование личностно ориентированных образовательных технологий с модульным построением изучаемого материала. Такой подход дает возможность выстраивания индивидуальных траекторий обучения и вариативного освоения программы математического курса. При этом учебно-воспитательный процесс можно объединить вокруг следующих основных идей: планирования результатов обучения, укрупнения дидактических единиц, организации учебного процесса с учетом психологических факторов, использования информационно-коммуникационных технологий.

При проектировании новых систем обучения в вузе с технологической ори- ентацией важно исходить из целостности представления образовательного процесса, рассматривая его в качестве управляемой педагогической системы, направленной на формирование у студентов знаний, умений, навыков, профессиональных компетенций и опыта творческой деятельности.

Для реализации педагогической стратегии необходимо разработать теоретическую модель обучения, технологическую карту организации учебного процесса на основе применения современных средств, методов и форм обучения, фонда оценочных средств. При этом нормативными документами для проектирования технологий и методических систем обучения должны являться рабочие программы дисциплины и образовательные стандарты.

В связи с введением новых федеральных государственных образовательных стандартов обозначились проблемы методики обучения математике в вузах. При переходе на двухступенчатую систему образования на многих направлениях подготовки уменьшилось количество часов, выделяемых на изучение математических курсов. Следствием этого стало изменение тематического содержания рабочих программ по преподаваемым дисциплинам, что в свою очередь не могло не затронуть и междисциплинарные связи. Перед педагогами обозначились актуальные проблемы: что преподавать, как преподавать и в каком объеме.

В связи с обозначенными проблемами пересмотр методов, средств и содержания обучения студентов университета является актуальным и имеет практическую значимость. Указанными факторами обусловлена цель данного исследования: обоснование эффективности комплексного использования в образовательном процессе вуза электронных курсов, авторских учебно-методических пособий, компьютерных тестов и методики выделения ключевых примеров в системах математических задач при обучении математике студентов агроинженерных направлений подготовки университета.

Обзор литературы

Различным аспектам обучения математике в вузе и средней школе посвящено немало работ отечественных ученых (О. Ю. Заславской [1], А. Е. Поличка [2], М. А. Родионова2, Г. И. Саранцева [3] и др.). Методика преподавания математики за рубежом чаще всего основывается на узкой специализации, рассмотрении конкретных примеров. В отечественной педагогике серьезное внимание уделяется глобальным проблемам развития индивидуальных способностей обучаемых и различным подходам в усвоении теоретического и практического учебного материала (Э. К. Брейтигам [4], Т. В. Смолеусова [5], Р. А. Утеева [6], Е. К. Хеннер [7], Р. Ш. Царева, С. А. Царев [8] и др.). В частности, Н. И. Поповым и А. Н. Марасановым рассматривалась методика выявления ключевых примеров и упражнений систем математических задач с последующим построением круговых диаграмм сильных связей между заданиями. Методика основывается на корреляционном анализе, цель которого ‒ определение степени тесноты связей между математическими задачами при помощи специального критерия, характеризующего надежность этих связей [9].

В современных условиях от специалиста требуется не только умение решать организационно-управленческие и производственные задачи, ему необходимы знания и навыки в использовании новых информационных технологий в своей профессиональной деятельности. Информационные технологии в подготовке бакалавров и магистров разных направлений приобретают фундаментальный характер. Кроме того, они активно используются при разработке экспертных систем [10] и интеллектуальных игр [11]. Применение информационно-коммуникационных технологий подразумевает проектирование новых форм и методик обучения с целью повышения эффективности образовательного процесса в высшем учебном заведении (М. А. Родионов [12], Т. Н. Суворова [13], О. М. Гущина, О. П. Михеева [14], М. Д’Соуза, П. Родригес [15], К. Кедрака, Г. Ротиди [16]).

Современная методика обучения математике опирается на «модели инновационного обучения, позволяющие синтезировать новые методические подходы и идеи, внедрять эффективные организационные наработки», которые помогают педагогу-математику управлять учебным процессом с целью получения оптимальных запланированных результатов [17; 18]. В соответствии с требованиями образовательных стандартов нового поколения, основные профессиональные образовательные программы математических курсов и специальных дисциплин в вузе направлены на повышение качества подготовки бакалавров и магистров на основе создания механизмов эффективного формирования у них компетенций, необходимых в дальнейшей профессиональной деятельности. Для решения такой стратегической образовательной задачи рабочие программы и новые курсы разрабатываются с опорой на вариативную часть учебного плана, предполагая при этом максимальное сближение профессиональной подготовки с производственной практикой в условиях конкретного региона.

Проблемам изучения и развития психолого-педагогических способностей обучаемых посвящено немало работ (М. Д’Соуза, П. Родригес [19], Су Чунг-Хо [20], Л. Робертс [21], А. В. Кудряшова, Т. Н. Горбатова, Н. Е. Рожкова [22] и др.). В настоящее время в рамках организации учебного процесса в вузе и средней школе активно используются диагностика интеллектуальных и профессиональных способностей обучаемых, различные виды компьютерного тестирования на этапах обучения. При этом Ч. Боднар, Р. Кларк акцентируют внимание на важности установления позитивных коммуникативных отношений между педагогом и учащимися в учебном процессе [23]. В работе С. Арнаба и С. Кларка отмечаются проблемы отсутствия в некоторых случаях полных методических рекомендаций при использовании информационных технологий в образовании [24]. А. А. Дворяткина и А. А. Дякина выделяют идеи проникновения гуманитарных и математических методов в различные области знаний [25].

Все вышесказанное подтверждает актуальность пересмотра методов, содержания и средств обучения студентов агроинже-нерных направлений подготовки университета в условиях реализации образовательных стандартов нового поколения.

Материалы и методы

Методология исследования опирается на обобщение зарубежного и отечественного педагогического опыта обучения студентов в вузах (Г. И. Саранцев [3], В. С. Се-нашенко [26], Р. Фелдер и соавторы [27], А. Моханти, Д. Даш [28], А. Джохри [29], Р. Лью, И. Хунг [30] и др). В процессе экспериментальной работы использовались методы эмпирического исследования: педагогический эксперимент, проведение педагогических измерений, экспериментальное обучение математике.

Курс высшей математики на агроин-женерных направлениях подготовки университета входит в базовый цикл дисциплин, поэтому изучается студентами на начальном этапе обучения. По нашему мнению, в условиях ранней специализации естественно было бы организовать процесс обучения с помощью методической системы, которая позволила бы студентам эффективно усваивать учебный материал, учитывая при этом межпредметные связи. В этом плане одним из приоритетных направлений является разработка и внедрение в учебный процесс электронных курсов и образовательных ресурсов. Курс высшей математики считается предшествующим для таких дисциплин, как статистические методы в земледелии, основы научных исследований в агрономии, программирование урожаев. Изучение таких предметов, как «Детали машин», «Сопротивление материалов», «Начертательная геометрия и инженерная графика», предполагает наличие базовых знаний и умений по векторной алгебре, аналитической геометрии. Без умений пользоваться математическим аппаратом статистического анализа невозможно освоить дисциплины «Экономическая теория», «Организация и управление производством». Изучение курса общей физики и теплотехники предполагает наличие базовых знаний по математическому анализу и дифференциальным уравнениям. Следовательно, рабочая программа курса математики на агроинженерных направлениях подготовки вуза должна разрабатываться с учетом разделов и тем, необходимых студентам в учебном процессе в дальнейшем.

Процесс обучения студентов Аграрно-технологического института Марийского государственного университета осуществлялся с использованием электронного курса «Математика», разработанного Е. Н. Никифоровой на базе платформы Learning Management System Moodle (LMS Mood-le), и с применением инструментов и сервисов электронного обучения. Курс включал в себя следующие модули:

– структурированный краткий теоретический материал;

– подробный разбор типовых практических заданий;

– тесты для самоконтроля;

– типовые задачи для самостоятельного решения с ответами;

– справочный материал3.

Для организации самостоятельной работы студентов и проведения практических занятий использовались учебники и учебно-методические пособия, в частности, специально разработанные авторами для агроинженерных направлений подготовки вуза: «Элементы линейной и векторной алгебры»4 и «Краткий курс дифференциального исчисления»5. Для проведения аттестации знаний студентов были составлены итоговые тесты, содержащие двадцать заданий и охватывающие следующие разделы рабочих программ курса математики:

– элементы линейной алгебры;

– элементы векторной алгебры;

– аналитическая геометрия на плоскости;

– аналитическая геометрия в пространстве;

– введение в анализ;

– неопределенный интеграл.

В статье приведены результаты исследований с использованием методических подходов, позволивших повысить итоговый показатель успеваемости студентов университета. В рамках экспериментальной работы обучающимся были предложены числовой и арифметический тесты для определения их способностей к анализу количественных данных, выявлению закономерностей, проведению вычислений и логическому рассуждению.

Для обработки результатов педагогического эксперимента были использованы аппарат статистического анализа и методика определения внутрипредметных связей в системах математических задач с применением корреляционного анализа.

Результаты исследования

Для эффективности обучения математике студентов агроинженерных направлений подготовки вуза целесообразно использование в учебном процессе электронного курса дисциплины. С учетом вышесказанного были предложены методические подходы при экспериментальном обучении математике студентов университета.

В своей преподавательской деятельности при работе со студентами-аграриями Е. Н. Никифоровой применялись репродуктивные, объяснительно-иллюстративные, частично-поисковые методы обучения, а также метод поэтапного формирования умственных действий. В качестве средств обучения использовались учебники, специализированные системы математических задач и упражнений, авторские учебно-методические пособия. Кроме того, был разработан и внедрен в образовательный процесс электронный курс «Математика» на базе платформы LMS Moodle, содержащий учебно-методические разработки дисциплины с модульным построением изучаемого материала.

При проведении опытно-экспериментальной работы со студентами существенным образом была использована методика выявления внутрипредметных связей, основанная на выделении ключевых примеров и упражнений в системах математических задач.

С целью определения уровня математических способностей студентов I–II курсов направлений подготовки «Агроинженерия», «Продукты питания животного происхождения», «Технология производства и переработки сельскохозяйственной продукции» ФГБОУ ВО «Марийский государственный университет» и студентов I курса по программам обучения «Электрификация и автоматизация сельского хозяйства», «Механизация сельского хозяйства» Йошкар-Олинского аграрного колледжа ФГБОУ ВО «Поволжский государственный технологический университет» было проведено тестирование с участием 147 респондентов. Для определения способностей к анализу количественных данных, проведению вычислений и логическому рассуждению были использованы числовой и арифметический тесты, включающие задания по воспроизведению закодированной числовой последо- вательности и требующие выполнения определенных математических операций. В течение фиксированного промежутка времени по числовому тесту студентам необходимо было выполнить максимальное количество заданий из 20 предложенных, а по арифметическому тесту – из 30 предложенных. Конечно, делать окончательные выводы об уровне математических способностей студентов по результатам двух тестов преждевременно, но уже на данном этапе исследования можно отметить следующее: высокие показатели тестируемых могут выявить скрытый потенциал для выбора той или иной профессии, в нашем случае инженерной, требующей умения анализировать узкоспециализированную информацию и проводить необходимые технические расчеты. Из статистических данных таблицы 1 следует, что по числовому тесту во всех академических группах средний показатель испытуемых соответствует способностям выше среднего, по арифметическому тесту также получены высокие результаты.

Для проведения аттестации знаний студентов по изученным (вышеуказанным) разделам математики были использованы итоговые тесты, содержащие двадцать заданий. Результаты тестирования с указанием академических групп представлены в таблице 1.

Отметим, что переход на федеральные государственные образовательные стандарты нового поколения предполагает

Т а б л и ц а 1. Среднее количество выполненных студентами заданий по тестам

T a b l e 1. Average number of completed questions in all tests

Группа / Group	Количество студентов / The number of students	Среднее количество выполненных заданий / The average marks for completed questions
		Числовой тест / Find the pattern tests	Арифметический тест / Numeracy test	Итоговый тест (20 заданий) / Final test (20 questions)
ПП	28	8,82	16,32	16,96
ТС-12	20	8,95	18,95	16,35
АИ-17	15	8,8	16,47	18,8
АИ-27	19	9,11	16,26	12,63
ТС-11	15	8,8	18,07	10,2
ТТО-11	27	7,26	12,96	9,85
ЭАСХ-11	23	8,48	14,26	10,78

необходимость организации учебной деятельности студентов с использованием интерактивных средств обучения. Электронный курс «Математика» был апробирован в 2015–2017 гг. при обучении студентов-аграриев Марийского государственного университета и Йошкар-Олинского аграрного колледжа. В ходе педагогического эксперимента в 2016–2017 гг. осуществлялось комплексное использование авторских учебно-методических пособий, электронного курса, компьютерных тестов и методики определения ключевых примеров и упражнений в системах математических задач. При обучении студентов математике в экспериментальных академических группах (ПП, ТС-12, АИ-17, ТС-11) Е. Н. Никифоровой применялся следующий подход: комплексное использование традиционной объяснительно-иллюстративной подачи учебного материала, электронного курса «Математика» и компьютерных тестов для проведения лекционных и практических занятий предполагало также применение в учебном процессе методики выявления ключевых примеров и упражнений в системах математических задач. В контрольных академических группах (АИ-27, ТТО-11, ЭАСХ-11) указанные методика и электронный курс не использовались.

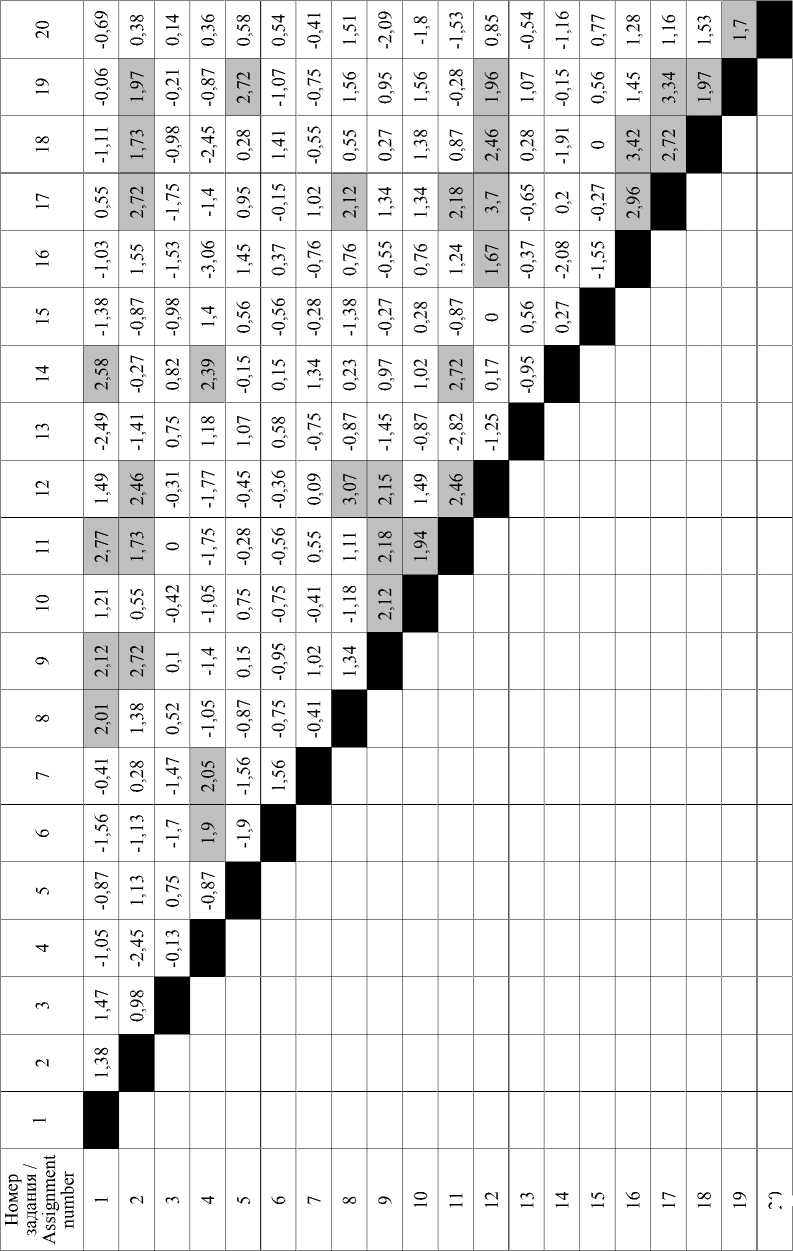
Как отмечалось ранее, для аттестации знаний студентов мы использовали тест, содержащий двадцать заданий из разных математических разделов рабочей программы. Результаты итогового тестирования в экспериментальных группах были подвергнуты тщательному анализу. В процессе исследования составлены сводные таблицы статистических данных, где для всех обучаемых указывались отметки о количестве правильно выполненных заданий. Кроме того, при анализе данных применялся метод сведения к дихотомии: баллы 0, 1, 2 и 3, выставленные за каждое задание, заменены на 0, а баллы 4 и 5 – на 1. Такая операция упрощает введение в память компьютера статистической информации. Далее для значений столбцов полученных таким образом ма- триц, состоящих из единиц и нулей, были вычислены коэффициенты корреляции, выражающие тесноту связей между заданиями данного теста, а также значения t-критерия достоверности этих связей [9]. Поскольку матрица значений t-критерия, элементы которой представлены в таблице 2, симметрична относительно главной диагонали, выделенной прямоугольниками, то таблица заполнена лишь наполовину. Значения t-критерия для малых выборок следует сравнивать с числом 1,64. Поэтому в таблице значения t при t ≥ 1,64 выделены темным фоном, для них достоверность вывода составляет не менее 90 %. Последнее означает, что связь между такими заданиями значимая, сильная и очень сильная6.

На основе данных таблицы 2 была построена круговая диаграмма сильных связей между заданиями итогового теста (рис. 1). Номерам кружков на ней соответствуют номера заданий теста. Если между заданиями существует сильная связь, что соответствует значениям t ≥ 1,64, то круги с такими номерами соединены сплошными линиями, если связь слабая – пунктирными. Во избежание излишней громоздкости и для наглядности диаграммы на рисунке 1 обозначены лишь три пунктирные линии.

На представленной схеме кружочками с темным фоном обозначены задания, имеющие много связей с другими упражнениями теста и невысокий средний балл при выполнении студентами. В нашем случае, это задачи № 2 и № 19, имеющие по шесть сильных связей, № 9 и № 18 – по пять, № 11 и № 17 – по семь, № 12 – восемь. Обратим внимание на задачу № 12, которая имеет наибольшее количество связей, а именно с заданиями № 2, 8, 9, 11, 16, 17, 18, 19 из раздела «Введение в анализ». В данном случае наличие большого количества связей обусловлено тем, что последние указанные задания из теста относятся к одному разделу математики. Если на консультации со студентами задаче № 12 уделить особое внимание в плане теоретического разбора учебного материа-

Т а б л и ц а 2. Матрица значений t -критерия

T a b l e 2. T -criteria matrix of values

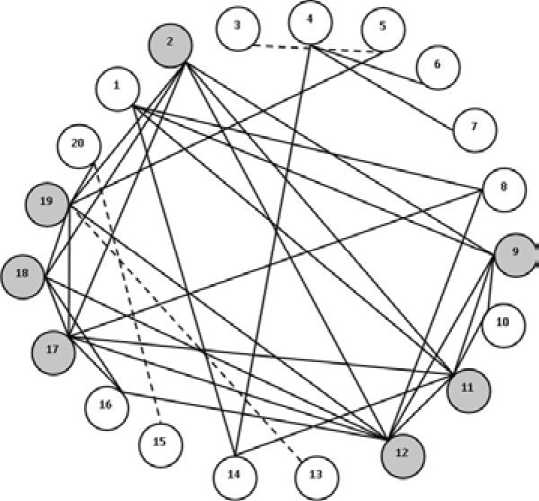
Р и с. 1. Круговая диаграмма связей между заданиями теста F i g. 1. Сircular diagram of the inter-links of the test questions

ла и практического закрепления умений и навыков решения такого типа задач, то, на наш взгляд, это должно улучшить результаты выполнения не только самого задания № 12, но и тех упражнений, с которыми данное задание имеет сильные связи. Поэтому подобные задачи, а в нашем случае еще и примеры № 2, 9, 11, 17, 18, 19, можно назвать ключевыми для предложенного теста.

Использование электронного курса «Математика», методики определения ключевых примеров в системах математических задач, авторских учебно-методических пособий при обучении студентов позволило в 2017 г. получить более высокие показатели в экспериментальных группах по сравнению с контрольными по среднему количеству выполненных обучаемыми заданий по итоговому математическому тесту (рис. 2). При этом отметим, что в экспериментальной и контрольной группах студенты примерно одинаково справились с числовым тестом, предложенным обучаемым в начальной стадии опытно-экспериментальной работы.

Педагогические эксперименты, проведенные ранее, также подтвердили, что выделение ключевых примеров и упражнений в системах математических задач и их наработка позволяют повысить качество знаний обучаемых7.

Обсуждение и заключения

При экспериментальном обучении математике студентов агроинженерных направлений подготовки вуза Е. Н. Никифоровой было осуществлено комплексное использование в образовательном процессе электронного курса, учебно-методических пособий, компьютерных тестов и методики выделения ключевых примеров в системах математических задач. После изучения курса высшей математики было проведено итоговое тестирование студентов. В результате в экспериментальных группах были получены более высокие показатели по сравнению с контрольными. Если в контрольных группах обучаемые успешно решали в среднем 55 % предложенных задач, то в экспериментальных группах – 78 %. Исследования, прове-

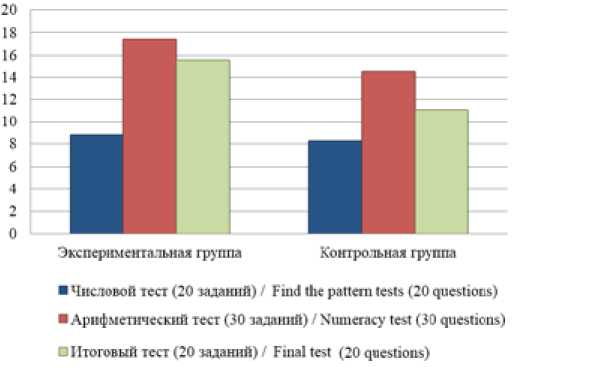
Р и с. 2. Среднее количество решенных задач студентами экспериментальной и контрольной групп

F i g. 2. Average number of completed questions in experimental and control groups денные в 2015–2017 гг., подтвердили, что предложенные авторами методические подходы эффективно влияют на усвоение обучаемыми теоретического и практического учебного материала, тем самым обоснована возможность и целесообразность их внедрения в образовательный процесс университета. Таким образом, основная цель экспериментального исследования достигнута.

Отметим, что необходимо обращать особое внимание студентов на межпредметные и внутрипредметные связи дисциплины при обучении математике. Они способствуют установлению логических связей между математическими понятиями, развитию аналитического мышления обучаемых и, в конечном счете, формированию у студентов научного мировоззрения.

При проведении исследований мы опирались на методику выявления вну-трипредметных связей с использованием ключевых примеров и упражнений в системах математических задач. Как подтвердила опытно-экспериментальная ра-

бота, указанные примеры имеют много пересечений с другими заданиями контрольных работ и тестов, поэтому им необходимо уделять особое внимание при теоретическом разборе изучаемого материала, а также закреплении умений и навыков решения задач на практике. Круговые диаграммы сильных связей между математическими заданиями наглядно иллюстрируют, каким именно конкретным задачам преподаватель должен уделить пристальное внимание на консультациях с целью повышения качества знаний обучаемых.

Результаты экспериментальной работы будут полезными для педагогов-предметников и работников системы образования. Считаем, что методические подходы, использованные при обучении студентов математике, в своей профессиональной деятельности могут успешно применять, в частности, преподаватели физики, химии и биологии в высшем учебном заведении и средней общеобразовательной школе.

СПИСОК

ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Поступила 19.07.2017; принята к публикации 24.11.2017; опубликована онлайн 30.03.2018.

Об авторах :

Попов Николай Иванович, заведующий кафедрой физико-математического и информационного образования ФГБОУ ВО «Сыктывкарский государственный университет им. Питирима Сорокина» (167001, г. Сыктывкар, Октябрьский пр., д. 55), доктор педагогических наук, кандидат физико-математических наук, ORCID: , Researcher ID: P-7428-2015,

Hикифорова Елена Hиколаевна, старший преподаватель кафедры математического анализа и теории функций ФГБОУ ВО «Марийский государственный университет» (424000, г. Йошкар-Ола, пл. Ленина, д. 1), ORCID: , Researcher ID: P-8776-2015,

Заявленный вклад авторов :

Попов Н. И. – научное руководство; развитие методологии; администратор проекта; критический анализ и доработка текста.

Никифорова Е. Н. – представление данных в тексте; компьютерные работы; подготовка начального варианта текста; проведение экспериментов.

Все авторы прочитали и одобрили окончательный вариант рукописи.

REFERENСES

Nikolay I. Popov, Head of Сhair of Physico-Mathematical and IT Education, Pitirim Sorokin Syktyvkar State University (55 Oktyabarskiy Prospekt, Syktyvkar 167001, Russia), (Pedagogy), Ph.D. (Physics and Mathematics), ORCID: , Researcher ID: P-7428-2015,

Elena N. Nikiforova, Seniour Lecture of Сhair of Mathematical Analysis and Theory of Functions, Mari State University (1 Lenin Sq., Yoshkar-Ola 424000, Russia), ORCID: , Researcher ID: P-8776-2015,

Contribution of the authors :

Popov N.I. – research and project management; development of methodology; critical analysis and final editing the text.

Nikiforova E.N. – collecting the data; computer processing; writing the draft; conducting the experiment.

All authors have read and approved the final manuscript .