Методика обучения будущих учителей математики решению текстовых задач

Одним из главных вопросов методики преподавания математики является формирование у обучающихся умений и навыков решения текстовых задач. Подобные задачи способствуют развитию у субъектов образовательного процесса умений применять знания, приобретённые ими при изучении математики, для решения проблем, возникающих в повседневной жизни.

Текстовые задачи выполняют различные функции в процессе обучения математике. Они являются эффективным средством для усвоения обучающимися терминов и понятий, играют огромную роль в воспитании, в развитии мышления, в формировании умений и навыков практического применения математики. Это одна из причин того, почему изучению текстовых задач отводится значительное место в курсах точных наук.

Задачи в математике в целом являются одновременно и целью, и методом преподавания. Решение позволяет формировать у обучающихся систему математических знаний, развивать творческое мышление, способствует развитию интеллекта и повышает уровень познавательных потребностей в обучении. Однако при всей пользе такого метода имеет место некий парадокс, заключающийся в том, что современные молодые люди испытывают сильные отрицательные эмоции при необходимости решить задачу – около половины обучающихся на контрольной работе или экзамене даже не приступают к этому сложному, на их взгляд, процессу.

Анализ результатов Единого государственного экзамена (ЕГЭ) по математике показывает, что с решением текстовых задач в среднем справляются 30 % учащихся. Большинство старшеклассников просто не знают, как это делать. Причиной всему является то, что учителя математики, зная о роли различных методов решения текстовых задач в развитии мышления учащихся, все же не используют их в полной мере в преподавании школьного курса математики, так как и сами не владеют необходимыми для этого знаниями и умениями. Очевидно, что истоки проблемы следует искать в вузовском образовании, не обеспечивающем качественную подготовку будущих учителей математики к обучению решению текстовых задач различными методами.

Процесс решения интересующих нас задач в методике преподавания математики делят на четыре ступени:

• 1.    Осмысление условия задачи.

• 2.    Составление плана решения задачи.

• 3.    Осуществление плана решения.

• 4.    Изучение найденного решения [1].

Л.М. Фридман определяет текстовые задачи из курса математики как словесные модели, в которых требуется найти значение одной или нескольких величин через известные данные других величин, имеющих с искомой те или иные взаимные связи [2].

Методика обучения решению текстовых задач отражена в трудах таких учёных, как Р.Ю. Костюченко [3], Е.И. Лященко [4], А.С. Монгуш [5], Д. Пойа [6] и других.

На занятиях по математике задействуются все существующие формы мышления: понятия, суждения, умозаключения [7]. Для того чтобы научиться решать текстовые задачи, нужно их просто решать – решать разные задачи, используя доступные способы, анализируя все возможные варианты, сравнивая их. В результате такой регулярной работы обучающиеся обнаружат преимущества и недостатки всех существующих приемов решения подобных задач и выберут для себя наиболее подходящий.

В психолого-педагогических и методических исследованиях отмечается также необходимость использования в обучении общих подходов к задаче как к объекту изучения, ее анализу и поиску решений. В соответствии с этим преподаватель ориентирован на формирование у обучающихся такого подхода к решению текстовых задач, при котором любая из них стала бы рассматриваться в качестве объекта для анализа или исследования, а ее решение заключалось бы в конструировании и изобретении способа нахождения ответа [8].

Существует шесть этапов решения текстовой задачи (рис. 1).

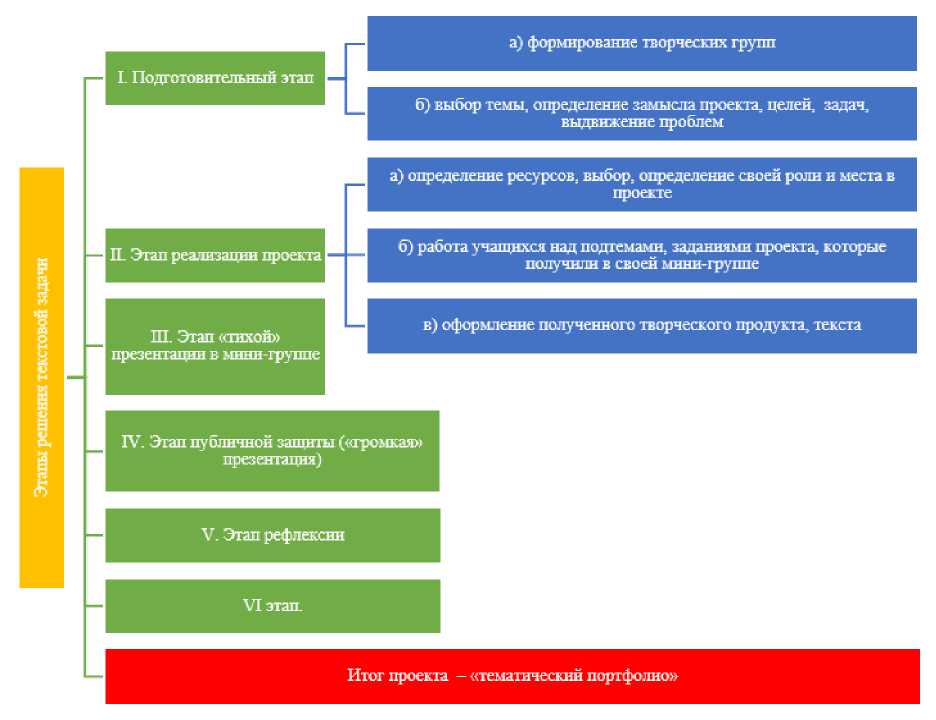
Рисунок 1 – Основные этапы решения текстовой задачи

Рассмотрим более подробно действия преподавателя и обучающихся с целью эффективного решения текстовой задачи.

• I.    Подготовительный этап:

• –    действия преподавателя: для работы над проектом предлагает студентам разбиться на 4 группы и выбрать темы;

• –    действия студентов: делятся на группы в соответствии со своими интересами, выбирают темы из предложенных преподавателем.

• II.    Этап реализации проекта:

• –    действия преподавателя: предлагает студентам найти информацию по выбранной теме;

• –    действия студентов: работают с источниками информации.

• III.    Этап «тихой» презентации в мини-группе:

• –    действия преподавателя: проводит «тихую» проверку, редактирует, уточняет и детализирует, указывая обучающимся на недочеты;

• –    действия студентов: первый раз в мини-группе представляют свой продукт в виде текста.

• IV.    Этап публичной защиты («громкая» презентация):

• –    действия преподавателя: на данном этапе работы он является экспертом, который производит оценку представленных докладов и выступлений обучающихся в целом;

• –    действия студентов: защищают подготовленный доклад.

• V.    Этап рефлексии:

• –    действия преподавателя: оценивает итоговую работу таким образом, чтобы каждому были понятны его ошибки или удачные решения;

• –    действия студентов: анализируют выступления одногруппников, а также роль каждого в создании итогового проекта.

• VI    этап. Итог проекта – «тематический портфолио»:

• –    действия преподавателя: выступает в роли тьютора;

• –    действия студентов: представляют оформленный продукт проекта в виде текста [9].

Практика преподавания показывает, что математику любят те обучающиеся, которые умеют решать текстовые задачи. И это наводит на мысль о том, что можно привить интерес к математике всем студентам, если научить их решать задачи. При правильном построении процесса у обучающихся развивается наблюдательность, сообразительность, находчивость, смекалка, логическое и абстрактное мышление, умение применять теорию к решению конкретных задач, а также происходит закрепление на практике приобретенных знаний [10].

Сказанное свидетельствует о том, что решение задач должно быть включено в каждое занятие по математике. Особое значение эта рекомендация имеет именно для студентов педагогических вузов, обучающихся по специальности «Математика» с тем, чтобы будущие учителя и сами умели решать текстовые задачи, и могли научить этому школьников. Тем более что в ходе решения задач общее развитие молодых людей (и студентов, и учеников общеобразовательных школ) получает дополнительный стимул за счет развития логики и мышления [11]. Изучение методики обучения будущих учителей математики решению текстовых задач в свете широты применения сегодня в образовательном процессе дистанционных технологий, предполагающих текстовую форму заданий, лишь подчеркивает актуальность данного процесса в современных условиях преподавания математики.

Ссылки:

• 1.    Аминова З.А. Методические особенности решения текстовых задач по математике // Вестник Череповецкого государственного университета. 2012. № 4-2 (43). С. 110–113.

• 2.  Фридман Л.М. Сюжетные задачи по математике. История, теория, методика. М., 2002. 204 с.

• 3.  Костюченко Р.Ю. Методика обучения учащихся решению математических задач: содержание этапов решения//

  Вестник Сибирского института бизнеса и информационных технологий. 2018. № 4 (28). С. 117–123.

• 4.  Лабораторные и практические работы по методике преподавания математики / Е.И. Лященко [и др.]. М., 1988. 223с.

• 5.  Монгуш А.С., Танова О.М. О методике обучения решению задач ЕГЭ с социально-экономическим содержанием//

  Вестник Тувинского государственного университета. Педагогические науки. 2015. № 4 (27). С. 65–71.

• 6.    Пойа Дж. Математическое открытие. Решение задач: основные понятия, изучение и преподавание. М., 1976. 448 с.

• 7.   Менчинская Н.А., Моро М.И. Вопросы методики и психологии обучения арифметике в начальных классах. М., 1965. 224 с.

• 8.   Генкин Г.З., Глейзер Л.П. Преподавание в классе с углубленным изучением математики // Математика в школе. 1991.

• 9.    Далингер В.А. Совершенствование процесса обучения студентов решению текстовых задач // Омский научный вестник. 2011. № 2 (96). С. 168–170.

• 10.    Забрамная С.Д., Исаева Т.Н. Некоторые психолого-педагогические показатели разграничения степеней умственной отсталости у детей на начальном этапе школьного обучения // Коррекционная педагогика: теория и практика. 2008. № 1 (25). С. 5–13.

• 11.    Митенева С.Ф. Роль математики в развитии логического мышления школьников // Современные вопросы науки и образования – XXI век : сборник научных трудов по материалам Международной заочной научно-практической конференции: в 7 частях. Ч. 5. Тамбов, 2012. C. 93–94.

№ 1. С. 20–22.

Редактор: Ситникова Ольга Валериевна Переводчик: Кочетова Дарья Андреевна