Методика обучения будущих учителей начальных классов решению косвенных задач при обучении математике

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 373..1.                                          

Задача, в которой два числа относятся к одному и тому же объекту, а требование (вопрос) которой запрашивает количества второго объекта, называется задачей, выраженной в косвенной форме [3].

Поэтому в таких задачах один и тот же объект обозначается двумя числами: первое число — это числовая характеристика данного объекта, а второе число — числовое отношение первого объекта ко второму. При этом о количественных характеристиках

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №5 2025 второго объекта не упоминается. По требованию задачи ее следует найти. В текстах таких задач используются слова «это», «их», «больше», «больше в раз», «меньше» и «меньше в раз».

Л. Н. Скаткин в своей педагогической теории подчеркивал важность использования косвенных (косвенно-практических) задач при обучении математике [4]. Его взгляд на этот вопрос заключается в следующем. Косвенные задачи — это задачи, которые требуют от учеников не только применения математических знаний, но и развития творческого, логического мышления, а также способности применять теоретические знания на практике. Такие задачи помогают учащимся глубже осмысливать материал и развивать навыки решения проблем в реальных условиях. Обучение математике должно быть направлено не только на усвоение формул и теорий, но и на развитие способности к абстрактному и логическому мышлению, а также на формирование умений решать более сложные и нестандартные задачи. Важным аспектом его методики является использование косвенных задач, через которые ученики учат применять математику в различных жизненных ситуациях, тем самым развивая аналитические способности и практические навыки. Через такие задачи можно обучать учащихся не только математическим методам, но и развивать их способность к самостоятельному поиску решений, что является важной частью педагогической практики. Задачи на увеличение (уменьшение) числа на несколько единиц или на увеличение (уменьшение) числа в несколько раз, содержащие словосочетания «это больше на», «это меньше на», «это больше во столько раз» и «это меньше во столько раз», выраженные в кос-венной форме обозначается в общем случае, при помощью стрелки в виде ломаной линии:

А. В. Белошистая в контексте преподавания математики также высказывала свои взгляды по поводу моделей и их применения в обучении [2]. Взгляды А. В. Белошистой по использованию моделей:

Создание и использование моделей — это наиболее эффективный способ абстрагирования математических понятий. подчеркивается, что использование моделей помогает наглядно объяснить абстрактные идеи, делая их более доступными для понимания. Модели помогают упростить сложные математические концепции и связывают их с реальным опытом учащихся.

Роль моделей в косвенных задачах — А. В. Белошистая предложила использовать модели как средство для решения косвенных задач. Через модели дети могут научиться применять математические методы и понятия на практике. Модели помогают развивать логическое мышление, показывают, как теория применяется в реальной жизни и дают возможность учащимся работать с абстрактными задачами.

К. Байгазиев при обучении математике придавал большое значение использованию косвенных (косвенных) задач [1]. Он утверждал, что такие задачи играют важную роль в математическом обучении по следующим причинам:

Развитие логического мышления : косвенные задачи способствуют развитию логического, аналитического и творческого мышления учащихся. С помощью таких задач ученики учат решать абстрактные проблемы на практическом уровне.

Глубокое понимание математических понятий: косвенные задачи помогают учащимся более глубоко понять математические принципы и методы.

Улучшение навыков решения проблем : косвенные задачи помогают ученикам находить новые методы и стратегии для решения задач, что расширяет их математические горизонты [1].

Составные задачи, выраженные в косвенной форме на увеличение и уменьшение числа на несколько единиц (в раз).

Словесная модель задачи —ее текст.

На первой полке 13 книг. Это на 5 меньше, чем книг на второй полке. А на третьей полке в 2 раза больше книг, чем на второй. Сколько книг на трёх полках?

Высказывательная модель задачи:

• 1)    На I полке 13 книг;

  ► условие

  требование

  
  

• 2)    На I полке на 5 меньше, чем книг на II;

• 3)    На III полке в 2 раза больше книг, чем на II;

• 4)    Cколько книг на трёх полках?

Графическая модель задачи

• а)    Модель схематический чертёж.

13 штук

I полка–

? штук

2 раза

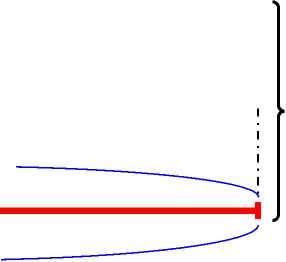
ii полка –

III полка –

• б)    модель схема

  
  
  

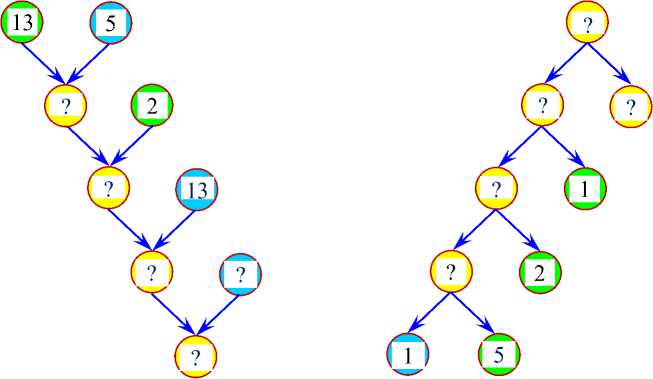
Математическая модель задачи:

13 штук — количество книг на I полке;

на 5 меньше — на I полке на столько меньше книг, чем на II;

(13+ 5) — количество книг на II полке;

(13+ 5) · 2 — количество книг на III полке;

((13+ 5) · 2 + 13) — количество книг на III полках;

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №5 2025

Решение:

• 13 + 5 = 18 штук — количество книг на II полке;

• 18 · 2 = 36 штук — количество книг на III полке;

• 36 + 13 = 49 штук — количество книг на I и III полках;

• 49 + 18 = 67 — количество книг на трёх полках.

Ответ: на трёх полках 67 книг.

Учителя начальных классов при обучении математике косвенным задачам должны использовать примеры из реальной жизни, а также обучать математическим моделям и методам решения. Учитель должен четко объяснять процесс решения задачи, показывать различные динамичные и практические примеры, развивая математическое мышление учеников. Важно также проверять понимание материала и учитывать индивидуальные интересы и уровень каждого ученика.