Методика проведения занятий на основе сочетания натурного и вычислительного эксперимента
Автор: Терегулов Денис Федорович, Попов Семен Евгеньевич
Журнал: Современная высшая школа: инновационный аспект @journal-rbiu
Рубрика: Инновационные технологии в вузе
Статья в выпуске: 4 (30), 2015 года.
Бесплатный доступ
Рассматривается проблема использования математического компьютерного моделирования при обучении будущих учителей физики. Выявлены три различных варианта эффективного сочетания натурного и вычислительного эксперимента. Даются краткие методические рекомендации по их использованию, как при освоении теории, так и при обучении экспериментальному методу анализа протекания физических явлений. Основной акцент сделан на представлении структуры учебного исследования, организованного по схеме совмещенного натурно-вычислительного эксперимента. Излагается последовательность использования данного подхода при изучении явления теплопроводности в учебной физической лаборатории. Обсуждаются математические модели явления, приводится схема экспериментальной установки, описаны методы определения ее параметров и анализируется соответствие экспериментальных данных и табличных значений.
Методика обучения физике, лабораторный практикум, натурный эксперимент, вычислительный эксперимент, явление теплопроводности
Короткий адрес: https://sciup.org/14240002
IDR: 14240002 | УДК: 378.6 | DOI: 10.7442/2071-9620-2015-4-114-122
Текст научной статьи Методика проведения занятий на основе сочетания натурного и вычислительного эксперимента
В современных условиях одним из основных направлений модернизации высшего профессионального образования является внедрение в образовательный процесс компьютерной техники и развитие на ее основе соответствующих информационных технологий. В частности, при обучении физике широко используется математическое компьютерное моделирование – вычислительный эксперимент [3], который применяется как при освоении теории, так и при обучении экспериментальному методу изучения физических явлений в учебных лабораториях.
Вместе с тем, следует отметить, что методика обучения физике с использованием компьютерного моделирования в настоящее время интенсивно формируется и активно обсуждается во всех ее аспектах. Так, остается проблемным определение места компьютерного моделирования в лабораторном физическом практикуме, эффективное сочетание натурного и виртуального эксперимента [4].
Проведенное нами исследование позволило выявить три варианта сочетания натурного и вычислительного эксперимента при проведении занятий в учебной физической лаборатории [5].
Параллельное выполнение натурного и вычислительного эксперимента
Отличительной особенностью этого варианта является возможность сравнения результатов натурного и вычислительного эксперимента, после чего могут быть сделаны выводы о достоверности итогов в случае совпадения результатов или о необходимости вернуться к этапу планирования с целью выявления и устранения допущенных ошибок. В учебном процессе обращение к параллельному выполнению натурного и вычислительного экспериментов целесообразно на этапе знакомства учащихся с технологией компьютерного моделирования. Например, при исследовании движения тел в вязких и плотных средах.
Последовательное выполнение натурного и вычислительного эксперимента
На практике подобная схема учебного физического исследования реализуется из двух последовательно (поочередно) выполняемых экспериментов. При этом роль второго может сводиться как к расширению границ применимости первого, так и к углублению содержательной стороны исследования. Возможны две вариации предложенной схемы: проведение вычислительного эксперимента по результатам натурного (компьютерный эксперимент подбирается к уже проводимому классическому натурному эксперименту, дополняя его) и постановка натурного эксперимента по завершению вычислительного.
Так, при изучении электростатического поля на первом этапе выполняется натурный эксперимент с получением картины эквипотенциальных поверхностей и силовых линий для плоских и цилиндрических электродов. Использование одних моделирует электростатическое поле конденсатора, других – поле точечных зарядов одинаковых по величине и противоположных по знаку. На втором этапе работы учащиеся строят компьютерную модель и выполняют серию вычислительных экспериментов по изучению электростатического поля сложной конфигурации, образованного большим числом заряженных тел.
Совмещенный натурно-вычислительный эксперимент
В некоторых случаях реализации натурного эксперимента препятствует возникновение на определенном этапе работы «неопределяемого» параметра. При этом уже полученных результатов может быть достаточно для организации вычислительного эксперимента с целью нахождения нужного параметра. Это дает основание для появления возможности продолжения натурного опыта. Обобщенную модель такого эксперимента можно представить в виде схемы, изображенной на рис. 1.
Методика проведения занятий на основе сочетания натурного и вычислительного эксперимента
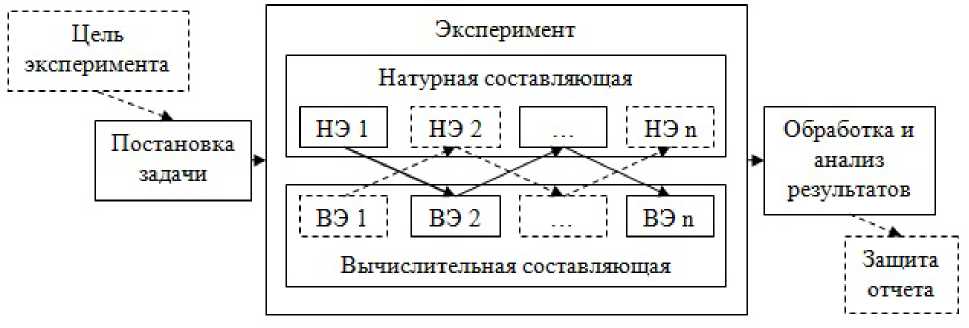
Рис. 1. Схема совмещенного натурно-вычислительного эксперимента
Учебные эксперименты, организованные по представленной схеме, имеют в методологическом плане максимальное соответствие структуре современных научных экспериментов. Их включение в содержание обучения будущих учителей физики оправдано и целесообразно.
Рассмотрим методику проведения занятия, организованного по схеме совмещенного натурно-вычислительного эксперимента на примере исследования явления теплопроводности металлов (таблица 1).
Таблица 1. Дидактическая структура натурно-вычислительного эксперимента
Д.Ф. Терегулов, С.Е. Попов
|
Этапы натурно-вычислительного эксперимента |
Содержание структурных этапов эксперимента |
Деятельность преподавателя |
Деятельность студентов |
|
Постановка задачи совмещенного эксперимента |
постановка задачи включает:
|
формулировка условий задачи; организация дискуссии относительно законов, лежащих в основе явления теплопроводности и их математического описания |
участие в беседе, конспектирование |
|
Натурный эксперимент |
проведение экспери мента:
точных результатов |
организация экспериментальной работы студентов:
|
измерения значений координат x ( x1 , x2 , x3 , x4 , x5 ) грузиков и времени их выпадения с каждого стержня t ( t1 , t2 , t3 , t4 , t5 ); повторение эксперимента несколько раз, вычисление средних значений времени tср |
|
Этапы натурно-вычислительного эксперимента |
Содержание структурных этапов эксперимента |
Деятельность преподавателя |
Деятельность студентов |
|
Вычислительный эксперимент для нахождения характеристик установки |
численное решение системы нелинейных уравнений для нахождения характеристик установки ( с и а ) |
помощь в проведении вычислительного эксперимента: 1) обсуждение алгоритма по решению систем уравнений с помощью блока функций Given/ Find ; 2) наблюдение и консультировании |
численное решение нелинейных уравнений с двумя неизвестными; актуализация учебного материала курсов «Информационные технологии», «Численные методы» |
|
Вычислительный эксперимент для нахождения коэффициента температуропроводности |
нахождение коэффициента температуропроводности (χ) |
обсуждение ал горитма решения уравнений с помощью встроенной функции root |
численное решение нелинейного уравнения с одной неизвестной |
|
Обработка и анализ результатов |
расчет значения коэффициента теплопроводности k . по известным величинам плотности и удельной теплоемкости образцов, а также найденному коэффициенту температуропроводности χ |
проверка результатов |
вычисление значений коэффициента теплопроводности k; оценка отклонений от табличных значений |
Натурно-вычислительный эксперимент начинается с выбора объекта изучения и формулировки цели [1; 2] – изучение теплопроводности металлов в нестационарном режиме, определение коэффициентов теплопроводности.
Постановка задачи совмещенного эксперимента
После выбора объекта исследования можно приступать к первому этапу, результатом которого будет содержательная постановка задачи. На этом этапе исследовательская деятельность студентов заключается в теоретическом изучении явления теплопроводности с целью выявления основных факторов, влияющих на его протекание, опреде-
лении соответствующих параметров, позволяющих описывать исследуемое явление. Основываясь на полученной информации об объекте исследования формулируется постановка задачи, которая в последующем может уточняться и конкретизироваться.
Однородные металлические стержни, нагреваются с одной стороны. Необходимо определить коэффициенты теплопроводности, фиксируя изменение показаний температуры различных точек стержней с течением времени.
Вслед за содержательной формулируется концептуальная постановка задачи. Это перечень вопросов о явлениях переноса, а также совокупность гипотез
Методика проведения занятий на основе сочетания натурного и вычислительного эксперимента
относительно законов протекания процесса теплопроводности:
-
1) процесс распространения тепла в образцах осуществляется путем теплообмена (конвекции нет);
-
2) поток тепла проходит в направлении, параллельном оси X (вдоль стержней);
-
3) с поверхности образцов часть тепла рассеивается в окружающую среду.
При отсутствии источников и стоков тепла распределение температуры вдоль металлического стержня можно описать классическим уравнением теплопрово- дности:
ат , а2г рс„— = к—-r v at а %?
Для учета стоков тепла (рассеяния тепла в окружающую среду) в уравнении (1) необходимо учесть поток тепла qc, отводимого с поверхности стержня. Так как разность температур тела и окружающей среды невелика, можно использовать уравнение Ньютона:
^ = ^-Г:) (2), где а - коэффициент внешней теплопроводности (α=b2рcv), Т – температура поверхности стержня, Т0 – температура окружающей среды. Для учета источни- ка тепла qu допустим, что количество теплоты, выделяемое им, полностью идет на нагревание:
(3), считая c, m постоянными величинами, и пренебрегая Т0 по сравнению с T, получим:
Д.Ф. Терегулов, С.Е. Попов
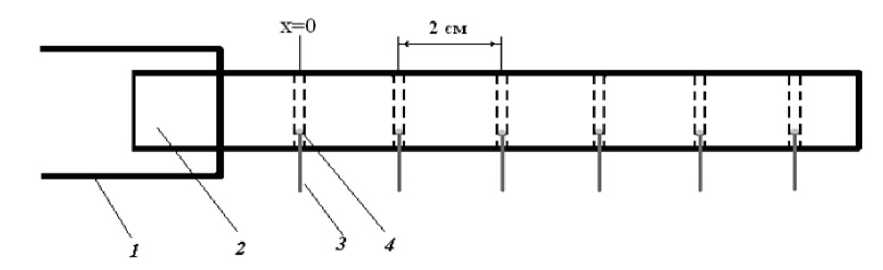
Рис. 2. Схема установки для определения зависимости T(x, t)
В нагревательный элемент (1) помещается исследуемый металлический (алюминиевый либо стальной) стержень – (2). В каждом стержне на расстояние два
Тогда уравнение теплопроводности для случая с источником и стоком будет иметь следующий вид:
^■■Т?= ^Р-'^ " <' " ^ (5).
Введем обозначения: (6),
_ к
Получим уравнение для распространения температуры (уравнение температуропроводности):
дт д2Т , „
7 7 -•'•:- (8), где х — коэффициент температуропроводности, T – температура в точке x в момент времени t. Это уравнение и является основой предлагаемого метода определения коэффициента теплопроводности в нестационарном режиме. Оно имеет следующее фундаментальное решение, которое подтверждается прямой подстановкой:
Т(х, t) = с—^=е 4xteat
Из уравнения (9) видно, что для определения характеристик теплопрово- дности нужно знать зависимость температуры различных частей стержня с течением времени. Для определения этой зависимости проводится натурный эксперимент.
Натурный эксперимент.
Схема экспериментальной установки представлена на рис. 2.
сантиметра друг от друга просверлены отверстия, в которые с помощью парафина (4) крепятся грузики равной массы («английские» булавки) – (3).
Перед проведением опыта необходимо растопить парафин. Затем, обмакивая в него шляпки «английских» булавок, закрепить их в отверстиях исследуемого стержня, как показано на рис. 2.
После включения установки стержень будет нагреваться и, когда температура около первого отверстия (точка отсчета по оси X ) будет равной температуре плавления парафина, грузик вы-
Таблица 2. Результаты натурного эксперимента
|
Алюминий |
Сталь |
|||||||||
|
№ опыта |
t1, (с) |
t2, (с) |
t3, (с) |
t4, (с) |
t5, (с) |
t1, (с) |
t2, (с) |
t3, (с) |
t4, (с) |
t5, (с) |
|
1 |
18.07 |
33.26 |
54.80 |
64.28 |
76.98 |
32.63 |
79.16 |
122.42 |
188.32 |
201.26 |
|
4 |
14.36 |
28.47 |
46.45 |
58.95 |
68.67 |
38.20 |
77.59 |
130.58 |
186.11 |
210.51 |
|
tср |
15.7 |
30.00 |
47.70 |
61.6 |
70.6 |
34.39 |
80.31 |
128.1 |
180.02 |
202.4 |
Учитывая, что за точку отсчета принимается момент выпадения первого груза, через t1 обозначено время выпадения второго грузика, t2 – третьего и т.д.
Вычислительный эксперимент для нахождения характеристик установки
Из уравнения (9) для источника в x 0 =0 видно, что температура зависит от координаты x , времени t , а также от характеристик установки (c, α) . Учитывая, что нагрев стержня по длине происходит неравномерно, одна и та же температура (плавления парафина) достигает определенных участков стержня за различное время. Так, T(x1, t1)=T(x2, t2) .
Составим уравнение:
^ Z1L xz2 (10).
-- р 4Xt2ga^^ = -- Р 4Xt2gat2 2Х.'ПХ^ 2jnXt2 "
Полученное равенство является нелинейным уравнением с двумя неизвестными, одно из которых – эмпирическая характеристика установки α. Для ее нахождения, применяется вычислительный блок Given/Find (Дано/Найти) универсального математического пакета падет из отверстия. В этот момент нужно включить секундомер для фиксации времени выпадения второго и последующих грузиков. Натурные эксперименты проводятся для стержней из алюминия и стали (таблица 2). Зная c, α, T(x, t) можно получить значения коэффициента температуропроводности χ, а, следовательно, и коэффициента теплопроводности k.
Mathcad. Алгоритм численного решения содержит последовательность действий:
-
1) задаются начальные приближения для всех неизвестных, входящих в уравнение (10);
-
2) вводится ключевое слово Given , указывающее, что далее следует уравнение;
-
3) записывается уравнение при помощи логических операторов панели Boolean (Булевы операторы);
-
4) вектору, составленному из решений, присваивается встроенная функция Find. При помощи итерационных методов Mathcad строит последовательность приближений, сходящуюся к искомому решению.
Используя найденное значение α и уравнение (9) вычисляется вторая характеристика установки с. Вычислительный эксперимент по нахождению значений α и с повторяется несколько раз для равенств: T(x2, t2)=T(x3, t3), T(x3, t3)=T(x4, t4), T(x4, t4)=T(x5, t5), T(x5, t5)=T(x1, t1).
Для исследуемых образцов средние значения α и c приведены в таблице 3.
Методика проведения занятий на основе сочетания натурного и вычислительного эксперимента
Таблица 3. Результаты вычислительного эксперимента
|
Алюминий |
Сталь |
|
|
α |
0,02 |
0,0093 |
|
c |
2,75 |
1,93 |
Из формулы (9) видно, что коэффициент температуропроводности не представляется возможным выразить в аналитическом виде, поэтому для его нахождения также применяются численные методы.
Вычислительный эксперимент для нахождения коэффициента температуропроводности
Нелинейное уравнение имеет одну неизвестную и может быть решено с ис- пользованием функции root(f(χ), χ), где f(x) — выражение, равное нулю, х — искомый аргумент.
Уравнение (9) представим в следующем виде: .
/"(у) = С—: е *xteat — Т
Для определения возможных решений строится график функции (рис. 3).
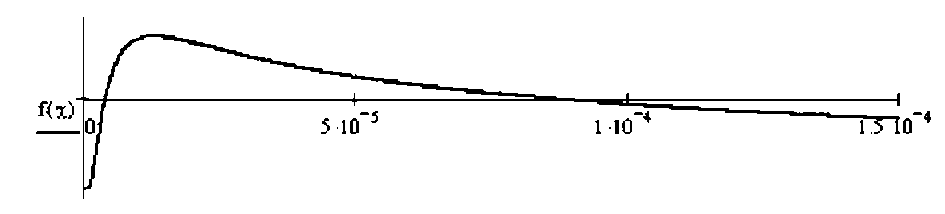
Рис. 3. Графическая оценка начальных приближений
Из графика – пересечение с осью абсцисс - находим начальное приближение и решаем уравнение относительно коэффициента температуропроводности χ :
, у = S,627 х 2 С"".
Обработка и анализ результатов
По найденным значениям коэффициента температуропроводности, известным величинам плотности и удельной теплоемкости вещества, рассчитывается значение коэффициента теплопроводности: (таблица 4).
Таблица 4. Результаты сравнения экспериментальных и табличных значений коэффициентов теплопроводности
Д.Ф. Терегулов, С.Е. Попов
|
Алюминий |
Сталь |
|||
|
эксперимент |
табл. |
эксперимент |
табл. |
|
|
k, Вт/м^К |
201,0 |
209,0 |
44,9 |
45,4 |
|
Отклонение в (%) |
3,8 % |
1,2 % |
||
|
Представленные материалы подтверждают, что вычислительный эксперимент эффективно дополняет натурный, расширяя границы его применения и обогащая новым содержанием. Методика обучения физике на основе сочетания натурного и вычислительного эксперимента обладает огромным потенциалом по формирова- |
нию профессиональной компетентности учителя физики и в значительной части ее информационной составляющей. Библиографический список: 1. Заковряшина О.В. Дидактические условия интеграции виртуального и натурного физического эксперимента // Физика в школе. 2012. № 7. С. 23-29. |
|||
-
2. Заяц М.Л., Попов С.Е. Технология проектного обучения основам вычислительного обучения студентов технических вузов // Вестник Орловского государственного университета. Новые гуманитарные исследования. 2011. № 2 (16). С. 135-138.
-
3. Заяц М.Л., Попов С.Е., Терегулов Д.Ф. Введение в Mathcad: учеб.-метод. пособие. Екатеринбург: УрГУПС, 2010. – 56 с.
-
4. Заяц М.Л., Попов С.Е., Терегулов Д.Ф. Специфика курсов компьютерного моделирования для студентов технических специальностей // Физическое образование в вузах. 2011. № 1. т. 17. С. 84-91.
-
5. Матвеев О.П., Фискинд Е.Э. Использование компьютеризированной лабораторной установки для проведения учебного исследования по оптике // Физическое образование в вузах. 2011. Т. 17. № 2. С. 90-96.
-
6. Попов С.Е. Концептуальные проблемы системы подготовки учителя фи
зики: Вычислительная физика // Физическое образование в вузах. 2005. № 3. т 11. С. 68-79.
-
7. Попов С.Е. Методическая система подготовки учителя в области вычислительной физики: Монография. Нижний Тагил: НТГСПА, 2005. – 227 с.
-
8. Старовиков М.И., Старовикова И.В. Натурно-вычислительный эксперимент в лабораторном практикуме по физике // Открытое и дистанционное образование. 2015. № 1. С. 70-77.
-
9. Терегулов Д.Ф. Модель информационной компетентности учителя физики // Фундаментальные исследования. 2014. № 12-10. С. 2235-2239.
-
10. Терегулов Д.Ф., Попов С.Е. Сочетание натурного и вычислительного эксперимента в лабораторном физическом практикуме // Современные проблемы науки и образования. 2015. № 1 // [Электронный ресурс]: www.science-education.ru .
Поступила 09.12.15
-
Об авторах:
Список литературы Методика проведения занятий на основе сочетания натурного и вычислительного эксперимента
- Заковряшина О.В. Дидактические условия интеграции виртуального и натурного физического эксперимента//Физика в школе. 2012. № 7. С. 23-29.
- Заяц М.Л., Попов С.Е. Технология проектного обучения основам вычислительного обучения студентов технических вузов//Вестник Орловского государственного университета. Новые гуманитарные исследования. 2011. № 2 (16). С. 135-138.
- Заяц М.Л., Попов С.Е., Терегулов Д.Ф. Введение в Mathcad: учеб.-метод. пособие. Екатеринбург: УрГУПС, 2010. -56 с.
- Заяц М.Л., Попов С.Е., Терегулов Д.Ф. Специфика курсов компьютерного моделирования для студентов технических специальностей//Физическое образование в вузах. 2011. № 1. т. 17. С. 84-91.
- Матвеев О.П., Фискинд Е.Э. Использование компьютеризированной лабораторной установки для проведения учебного исследования по оптике//Физическое образование в вузах. 2011. Т. 17. № 2. С. 90-96.
- Попов С.Е. Концептуальные проблемы системы подготовки учителя физики: Вычислительная физика//Физическое образование в вузах. 2005. № 3. т 11. С. 68-79.
- Попов С.Е. Методическая система подготовки учителя в области вычислительной физики: Монография. Нижний Тагил: НТГСПА, 2005. -227 с.
- Старовиков М.И., Старовикова И.В. Натурно-вычислительный эксперимент в лабораторном практикуме по физике//Открытое и дистанционное образование. 2015. № 1. С. 70-77.
- Терегулов Д.Ф. Модель информационной компетентности учителя физики//Фундаментальные исследования. 2014. № 12-10. С. 2235-2239.
- Терегулов Д.Ф., Попов С.Е. Сочетание натурного и вычислительного эксперимента в лабораторном физическом практикуме//Современные проблемы науки и образования. 2015. № 1//: www.scienceeducation.ru.
- Zakovryashina O.V. Didactic conditions of full-scale integration of virtual and physical experiment. Fizika v shkole. 2012. No. 7. P. 23-29.
- Zayats M.L., Popov S.E. Technology of design training to bases of computing training of students of technical colleges. Vestnik Orlovskogo gosudarstvennogo universiteta. Novye gumanitarnye issledovaniya. 2011. No 2 (16). P. 135-138.
- Zayats M.L., Popov S.E., Teregulov D.F. Introduction to Mathcad. Ekaterinburg, izd-vo. UrGUPS. 2010. P. 56.
- Zayats M.L., Popov S.E, Teregulov D.F. Specifics of rates of computer modeling for students of technical specialities. Fizicheskoe obrazovanie v vuzakh. 2011. No 1. P. 84-91.
- Matveev O.P., Fiskind E.E. The use of computerized laboratory setup for training research in optics. Fizicheskoie obrazovanie v vuzakh. 2011. No. 2. P. 90-96.
- Popov S.E. Conceptual problems of system of preparation of the teacher of physics: the Computational Physics. Fizicheskoe obrazovanie v vuzakh. 2005. No 3. P. 68-79.
- Popov C.E. Methodological system of teacher training in the field of Computational Physics. Nizhniy Tagil, izd-vo. NTGSPA. 2005. P. 227.
- Starovikov M.I., Starovikova I.V. Real-computational experiment in the laboratory workshop in physics. Otkrynoe i distantsionnoe obrazovanie. 2015. No 1. P. 70-77.
- Teregulov D.F. Model of informational competence of the teacher of physics. Fundamentalnyie issledovania. 2014. No. 12-10. P. 2235-2239.
- Teregulov D.F., Popov S.E. Combination of natural and computing experiment in the laboratory physical practical work. Sovremennye problemy nauki i obrazovaniya. 2015. No 1.//: www.science-education.ru.


