Миграция зоны наименьшего прогревания в гетерофазной модельной пищевой системе при стерилизации

Введение. Промышленную стерильность вырабатываемых консервов, гарантирующую микробиологическую стабильность и безопасность в течение установленного для них срока годности, должен обеспечивать выбор главных параметров режимов стерилизации – температуры продукта T(τ) и экспозиции τ и давления в упаковках.

Консервы отвечают требованиям промышленной стерильности, если фактическая летальность L процесса тепловой обработки продукта равна или превышает требуемую летальность F [1], т. е. L ≥ F .

L определяют в процессе тепловой обработки при измерении температуры продукта T(τ) в SHZ по формуле 1 [2], а F рассчитывают исходя из необходимого стерилизующего эффекта по формуле 2 [1]:

T~Tref

L = ∫7 10 ^z_∙ , (1)

F = D_T ∙( ig- ^{∙ v}- ^∙ ^ ^% ) , (2)

где Tref – референтная температура стерилизации для целевых микроорганизмов, °С; z – вариация температуры стерилизации при изменении времени термической смерти целевых микроорганизмов в 10 раз, °С; DТ – время десятикратного снижения численности стерилизуемых при температуре T целевых микроорганизмов (споровой суспензии), мин; С0 – начальная кон- центрация целевых микроорганизмов в стерилизуемой упаковке с продуктом, спор/см3; V0 – объем продукта в единице стерилизуемой упаковки, см3; S – допустимый микробиологический брак консервов, %.

Ключевым фактором теплообмена любой гетерофазной системы с жидкой дисперсионной средой, независимо от используемого алгоритма расчетов, является возможность возникновения и параметры развития конвективных течений в процессе тепловой обработки [3–5]. Динамика и выраженность этих явлений определяется целым спектром параметров, таких как вязкость, плотность, геометрия упаковки, объемная доля частиц дисперсной фазы и др.

Теплопередача в гетерофазных FS с дисперсной фазой значительно отличается по сравнению с жидкими пищевыми продуктами, потому что наличие твердых частиц в упаковке затрудняет движение жидкости за счет естественной конвекции, в результате чего SHZ мигрирует вверх.

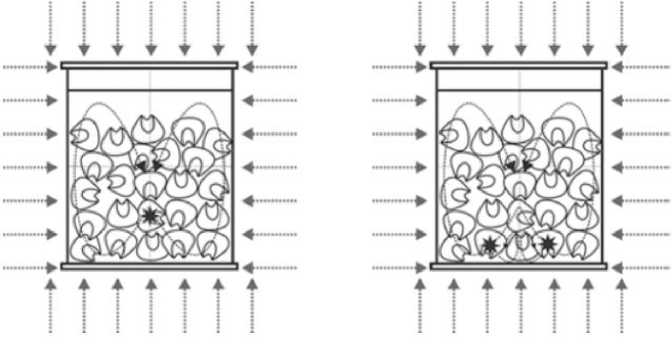
Авторы [6] считают, что в гетерофазных крупнодисперсных FS теплообмен теплопроводностью менее эффективен, чем теплопередача конвекцией. На рисунке 1, а схематично показано расположение SHZ для дисперсионной среды с высокой вязкостью. Она расположена, по мнению авторов [6], в частицах дисперсной фазы, лежащих по центральной оси банки выше, чем в случае с аналогичной системой, но с маловязкой дисперсионной средой (рис. 1, б).

а

б

Рис. 1. Схема расположения SHZ (*) в различных FS: а – гетерофазные продукты с вязкой дисперсионной средой; б – то же с маловязкой дисперсионной средой по данным [4]

Сложность выявления и идентификации SHZ гетерофазных продуктов в упаковках при тепловой обработке в связи с наличием вероятности ее миграции и величиной погрешности приборных экспериментальных методов исследований отмечена в работах [7–10].

Приведенный анализ методов установления и валидации режимов тепловой обработки показывает, что известные процедуры расчета режимов процесса, основанные на установлении значения L по температуре T в SHZ для гетерофазных консервируемых продуктов с жидкой дисперсионной средой, не обеспечивают необходимой точности.

Цель исследования – изучение зависимости динамики миграции SHZ в процессе стерилизации гетерофазных модельных FS в невовле-каемой в конвекционный поток дисперсной фазе от вязкости дисперсионной среды.

Задачи исследования. Учитывая недостаточную обоснованность и малую вариативность установления режимов стерилизации гетерофазных FS, актуальной задачей является выбор и проверка адекватности объективного фактора, более достоверно отражающего термическое воздействие на популяцию целевых микроорганизмов в упаковке с гетерофазными FS.

Объекты и методы исследования. В качестве объекта исследования использовали модельные FS с дисперсной фазой, состоящей из шариков Ø8 мм из стирол-акрило-нитрила (далее AS) с термостойкостью 103 °С, фактически измеренной плотностью 1,67 г/см³, массой по

0,4±0,05 г. Дисперсионная среда модельных систем включала: маловязкую, имитирующую заливку зеленого горошка (1,5 % водный раствор NaCl и сахарозы), и средневязкую – 11 % водный раствор сахарозы (относительная вязкость – 1,6 по сравнению с маловязкой средой).

Исследуемую среду помещали в стеклянные банки (тип III-52-190) для детского питания по ГОСТ 32671-2014, в 10 слоев общей высотой 74 мм и высотой свободного пространства до крышки 20 мм.

Рабочий спай МК термопары Ø 1,2 мм фиксировали на высоте 3; 6; 9; 12; 15 и 18 мм от дна по оси банки. Банку с FS, имевшей постоянную начальную температуру 30±0,1°С, прогревали в водяном циркуляционном термостате модели WCH-12 (Корея) при постоянной температуре со значениями 75; 80; 85; 90 и 95 °С в каждой из указанных зон измерений в трехкратной повторности. После термостатирования с экспозицией 20 мин банку помещали в холодную воду (t w = 21±0,1 ºС) для охлаждения на 10 мин.

Регистрировали температуру в зонах измерений автоматическим многоканальным термометром CTF9008 (Ellab) с дискретностью 30 с и передачей данных в СОМ-порт РС.

Для математической обработки экспериментальных данных для их аппроксимации функциями, соответствующими теплоинерционным свойствам FS, использовали ПО TableCurve 2D v.5.01 (SYSTAT Software Inc.), Wolfram Mathema-tica 10.4 и VBA MS Excel 2010.

Результаты исследования. Основным постулатом существующих подходов к установлению режимов термической стерилизации консервируемых FS является достаточность создания в SHZ условий гарантированной инактивации целевой микрофлоры. Базовым показателем, определяющим возможность создания таких условий, является динамика температуры FS в SHZ при стерилизации.

В гетерофазных FS с жидкой дисперсионной средой дополнительным возмущающим фактором являются твердые частицы дисперсной фазы. Наличие, размеры, объемная доля частиц дисперсной фазы предполагают нарушение ими

Вестник КрасГАУ. 2021. № 11 общей динамики тепловых конвекционных потоков, вследствие чего должны изменяться вид и выраженность локализации SHZ в процессе термической обработки [11, 12].

Анализ результатов экспериментальных данных температуры T(τ) в зонах FS по оси банки на разной высоте h показал неприемлемость использования показателя L в качестве первичной функции отклика для определения динамики миграции зоны наименьшего прогревания в исследуемых модельных системах в силу ее малой вариативности при изменениях температуры T st и h (рис. 2).

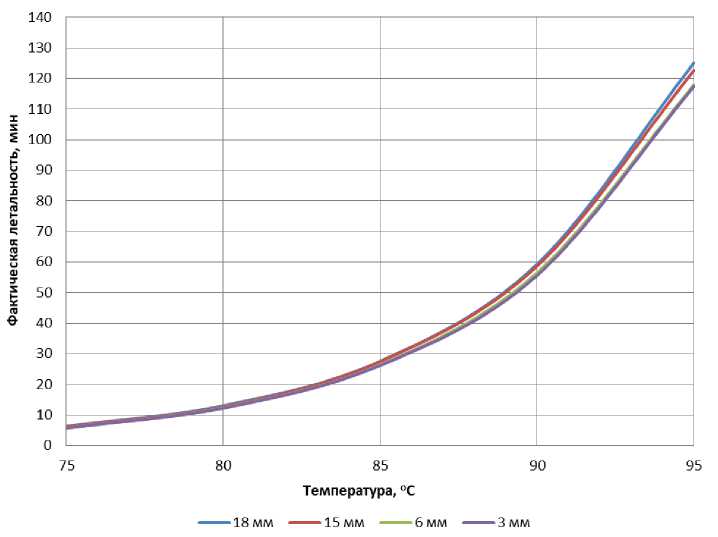
Рис. 2. Зависимости фактической летальности от температуры термостатирования в интервале значений геометрической высоты расположения термопары

По этой причине была изучена возможность использования метода, известного как «время установления системы» [13] к определению локализации SHZ в зависимости от T st . При стерилизации FS, расфасованного в герметичную упаковку, кривая з T(τ) в каждой дискретной точке объема представляет собой S-образную функцию времени τ , ограниченную двумя горизонтальными асимптотами. Для аппроксимации безразмерной температуры продукта θ(τ) эмпирическая функция имеет вид

0 (т) = ехр (- exp (-f (т))) , (3)

причем

в(т) = Т^- .          (4)

1 st- 1 о

Для упрощения аппроксимации значения температуры переводили в безразмерную логарифмическую форму D:

D (т) = -1п (-ln ( 0(т)) ) .      (5)

Нижнюю температурную границу принимали T 0 = 29 °С для всех исследованных значений T.

На основании преобразованных исходных данных численными методами была определе- на при помощи программы Table Curve аппрок симация зависимости D(t) функцией вида          T=exp(--exp(-(a+b*(1 -exp(-с*т))))y(Tst-To) + To. (7)

D(τ)=a+b·(1-ехр(с·θ)) ,  (6)

где a – безразмерная константа; b и c – безразмерные коэффициенты.

При этом полное математическое описание динамики температуры прогревов T в экспериментально заданных точках представляет собой функцию τ вида

Аппроксимирующая функция (7) имеет верхнюю горизонтальную асимптоту Tst, поэтому для определения продолжительности нагрева целесообразно взять реперное значение температуры, отстоящее от максимального на некоторую фиксированную величину ΔT (рис. 3), значение ΔT = 0,5 оС.

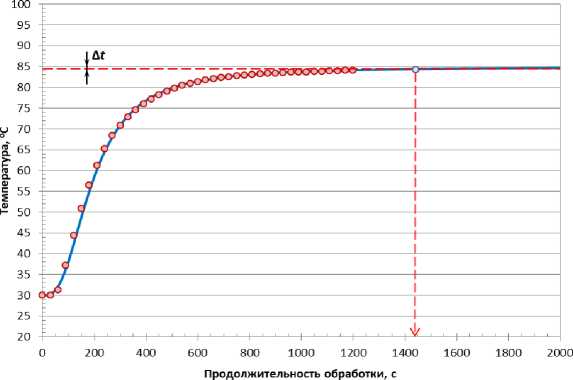
---Модель О Эксперимент

Рис. 3. Продолжительность нагрева на основании аппроксимации экспериментальных данных для реперной температуры T=T st –ΔТ

В этом случае продолжительность нагрева, при которой в исследуемой зоне достигается температура T st –ΔТ , рассчитывали как

=                  ,             (8)

Δ,

где         =-  (-             ) .    (9)

В соответствии с принятыми допущениями геометрической высоте локализации зоны наименьшего прогревания соответствует максимум продолжительности нагрева для достижения температуры T st – ΔТ. Данное условие соблюдается при равенстве производной функции нулю:

^′ =     ^{√        (  )}     =0․     (10)

√         (   )

Численными методами были определены локализации зон SHZ для каждого экспериментального значения T st . Полученное аналогичной аппроксимацией термограмм математическое описание зависимости геометрической высоты h SHZ локализации SHZ имеет следующий вид:

һ =            ,

где h – геометрическая высота локализации зоны наименьшего прогревания, мм; T – температура FS , °С; a – константа; b , c , d , e и f – коэффициенты.

Анализ результатов моделирования показывает, что в процессе нагревания в диапазоне от 70 до 78 оС имеет место незначительная миграция SHZ на ≈ 1,6 мм вниз, после чего дальнейшее увеличение температуры не приводит к сколько-нибудь существенной смене ее локализации (рис. 4).

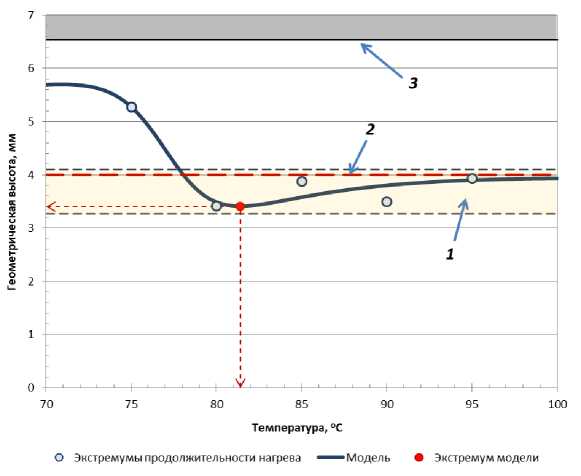
Рис. 4. Динамика изменения высоты расположения SHZ в процессе тепловой обработки: 1 – область девиации SHZ; 2 – горизонтальная ось I слоя;

3 – верхняя аксиальная граница ячейки, образованной тетраэдром частиц

Таким образом, искомая hSHZ = 2,53 мм над горизонтальной осью I слоя (рис. 5). В результате при температуре 75 °С SHZ локализована в свободной области пространства, заключенной между шариками I и II слоя вблизи вертикальной оси банки.

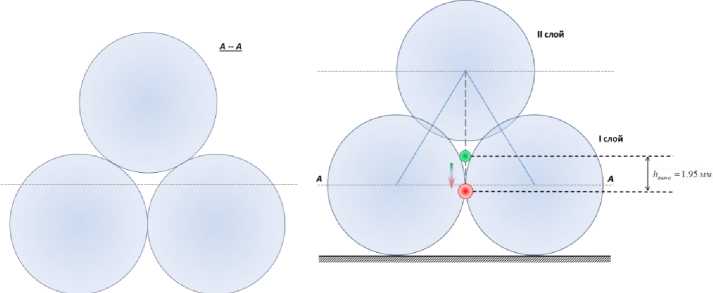
Рис. 5. Миграция SHZ в пределах слоев частиц дисперсной фазы для системы с 11 % раствором сахарозы

Математическое описание зависимости τ от h SHZ для всех исследованных значений T st имеет

Т ’ =

1, 5bh0-5 +2,5 ch 1’

(а+bh ^1,5+ch^2,5) ² = 0 .

вид

т =---—--— . а+bh 1 ■ 5+ с h 2 ■ 5

где a – константа; b и c – коэффициенты.

Тогда, по определению, существование SHZ для каждого значения T(τ) определено величиной h SHZ , при которой справедливо выражение

Расчетные данные о локализации SHZ при разных значениях T st могут быть адекватно аппроксимированы функцией вида:

(d+1 )

^hL Н Z = ^{a +}       -------j-----“2 ,   ⁽¹⁴⁾

t M+1) (d- 1 +^[d+1])

где a – константа; b , c и d – коэффициенты.

Результаты моделирования динамики ми-  исследованных FS представлены на рисунке 6.

грации SHZ в процессе тепловой обработки для

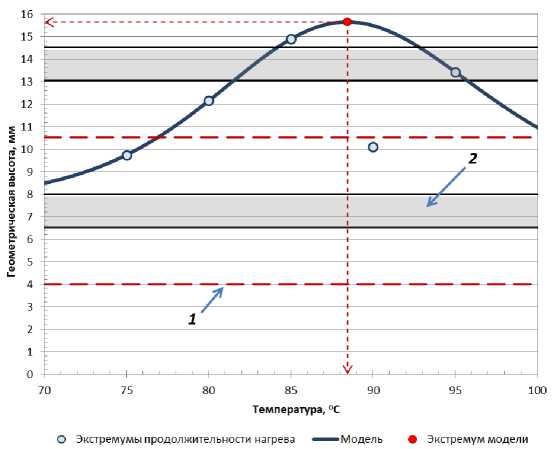
Рис. 6. Динамика миграции SHZ в процессе тепловой обработки:

1 – горизонтальная ось слоя; 2 – область суженного перехода между смежными по высоте ячейками, образованными сферическими частицами дисперсной фазы

Анализ результатов моделирования показал, что следствием замены дисперсионной среды на менее вязкую (в 1,6 раз) является значительное изменение динамики миграции SHZ при стерилизации. Так, при нижней границе исследованного температурного диапазона (75 °C) локализация SHZ смещена относительно другой FS в ячейку, образованную одной сферической частицей дисперсной фазы I слоя, тремя – II, и одной – III слоя.

При Tst → 95 °C и h → max и дальнейшей ее миграции через узкий межшаровой зазор в смежную ячейку, образованную шариком II слоя, тремя – III и одним – IV (рис. 7). После достижения h = max при T(τ) ≈ 87 °С при дальнейшем увеличении T(τ) направление миграции SHZ меняется на обратное.

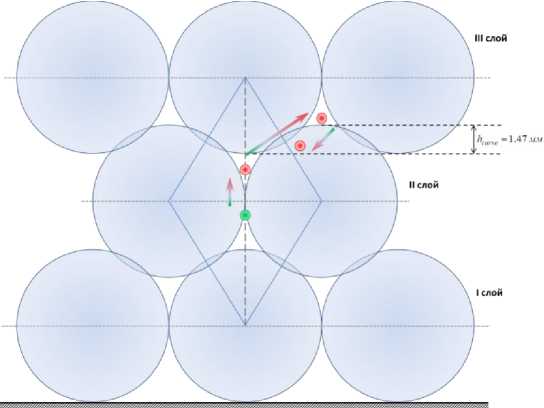
Рис. 7. Схема миграции SHZ в пределах слоев частиц дисперсной фазы FS с дисперсионной средой (1,5 % NaCl и 1,5 % сахарозы)

Таким образом, снижение вязкости дисперсионной среды в FS с не вовлекаемыми в конвекционные потоки частицами дисперсной фазы в 1,6 раз способствовало более свободному конвективному перемещению дисперсионной среды в процессе тепловой обработки. Это приводит к смещению диапазона миграции SHZ в область, вовлекающую более высоко расположенные ячейки, и увеличению интервала геометрической высоты h локализации SHZ в процессе миграции.

B результате проведенных исследований установлено, что в случае, когда дисперсность и плотность частиц твердой фазы не позволяет им быть вовлеченными в общий конвекционный поток, гетерофазная система ведет себя как ячеистая структура с суперпозицией конвективного и кондуктивного теплообмена. Поэтому диапазон миграции SHZ оказывается запертым между двумя-тремя слоями частиц дисперсной фазы, с уменьшением геометрической высоты h границ и диапазона миграции при увеличении начальной вязкости дисперсионной среды.

Выводы. Установленные закономерности миграции SHZ следует принять за основу методики определения кинетики прогревов гетерофазных FS с целью получения максимально адекватных данных для разработки режимов тепловой стерилизации со сниженной термической нагрузкой на FS.

Предложен используемый в технике измерений метод «времени установления системы» для оценки термического воздействия на популяцию целевых микроорганизмов в исследуемой зоне FS, основанный на расчете режима тепловой обработки по максимальному времени установления реперного значения температуры, зависящего от заданной температуры стерилизации T st и миграции исследуемой зоны в фазе нагрева.