Моделирование электромагнитного поля в горизонтально-слоистых радиально-неоднородных анизотропных средах

Изучение рассеивания электрических и магнитных полей в квази-трехмерных геологических структурах (например, в околоскважинном пространстве в методах геофизических исследований скважин) имеющих анизотропию по удельной электропроводности и магнитной проницаемости [1, 2] – практически значимая задача. В процессе бурения скважины вокруг ствола появляются ослабленные зоны, выражающиеся в образования радиальных и азимутальных трещин отрыва (необратимые деформации). К аналогичным изменениям околоскважинного пространства приводит фильтрация флюидов (обратимые процессы). Эти изменения околоскважинного пространства приводят к горизонтально-слоистой и радиально-неоднородной анизотропной модели геоэлектрической среды, обладающей осевой симметрией. К настоящему времени на основе аналитических решений достаточно полно исследованы одномерные радиально-неоднородные и горизонтально-слоистые модели [2, 3]. С использованием численных методов решение получили более сложные задачи – радиально неоднородные горизонтально-слоистые анизотропные, с наклонным расположением слоев [4].

В общем случае электрофизические параметры – удельная электропроводность и магнитная проницаемость, являются тензорами второго ранга. Они обладают частотной дисперсией, что требует нахождения решения прямой задачи в широком диапазоне частот – от первых герц до мегагерц с изменением толщин слоев как в вертикальном, так и в горизонтальном направлениях, начиная от первых миллиметров и сантиметров.

Важным приложением таких задач является разработка скважинной аппаратуры, где требуется учесть пространственные размеры источников и приемников, а также особенности конструкции скважинного снаряда, их физические и геометрические характеристики. Предварительное математическое моделирование позволяет разработать технические требования к скважинной аппаратуре, позволяющие решать конкретные геологические задачи. Одной из таких перспективных задач является задача поиска и исследования газогидратов, которые стандартными методами геофизических исследований скважин не выявляются. Особенностью газогидратов, широко распространенных в районах вечной мерзлоты, является дисперсия удельной электропроводности, проявляющаяся на высоких частотах [4].

1. Решение прямой задачи электродинамики в цилиндрической системе координат

Рассмотрим азимутально-однородную горизонтально-слоистую среду. Положим, что поле обладает осевой симметрией и не зависит от азимутальной координаты. Тогда система уравнений Максвелла для анизотропной среды в цилиндрической системе координат, записанная в частотной области, приобретет вид:

∂∂

Hr — ~^rHz + aeeEe + J , ∂z ∂r

∂

„dzH

‘d E^-E,

∂z∂r

∂

-a rr E r

ex

- J _r ,

-

i^P ee H e - iuB ex ,

—Ee = шц„ H r + iuB_r , ∂z

(ГдЕ '^{))) +    (} i^B ex ),

E z — —(1 у (rH )) - — J zx , σ zz r ∂r          σ zz ^z

H z — —( µ zz

-

где H _r , E _θ , H _z – компоненты электромагнитного поля в проекции на оси пространственных координат {r,d,z} (ось z направлена вниз, вглубь земли); a _rr ,a _ee ,a _zz - удельные электропроводности среды по радиальному, азимутальному и вертикальному направлениям, соответственно – комплексные функции частоты ω ; µ _rr , µ _θθ , µ _zz – магнитные проницаемости среды по радиальному, азимутальному и вертикальному направлениям, соответственно – также комплексные функции частоты ω ; J _r ^ex , J _θ ^ex , J _z ^ex – компоненты вектора стороннего электрического тока; B _r ^ex , B _θ ^ex , B _z ^ex – компоненты вектора сторонней магнитной индукции; i = ^/-1. Источники электромагнитного поля могут находиться как внутри скважины, так и в околоскважинном пространстве при условии сохранения осесимметричности задачи.

Воспользуемся преобразованием Фурье - Бесселя [5] порядка n: F(р) — ∞

IFJ^dr, для которого существует обратное преобразование F (r) ^— 0

∞

У F(p') J n (p ‘ r) р ‘ dp ’ , где J n (x) - функция Бесселя n-го порядка.

Найдем преобразование Фурье – Бесселя порядка n от правой части выражения d-Ez = дт 1(1 д (rHe)).

∂r      ∂r σ _zz r ∂r

Будем иметь

∞

[ ^д~ (—(1 Н е + ^Не IWpr'irdr ∂r σ _zz r ∂r

—Н е ((n + 1)J n (pr) — prJ n+i (pr)) | “ + / σ zz

= -(-H e + ^Не)J n (pr)r Г σ _zz r ∂r

∞

-

i Н е (-rp 2 + - σ zz

-

r

- )J n (pr)dr+

∞ d 1 + I (^--)Н е ((n + 1J n (pr) — prJ n+i (pr))dr.

∂r σ zz

Отсюда следует, что только в случае п ² = 1 можно воспользоваться интегралами Ломмеля [5] и, таким образом, вычислить интегралы по радиальной координате в явном виде через функции Бесселя. В противном случае интегралы в явном виде не имеют аналитического выражения и, в вычислительном плане, это создает сложную проблему.

∞

В силу этого полагаем Н _е = Н _е (r) = f Н _е (p ' )J ₁ (rp ' )pdp. Тогда

∞

∞∞

[ ^д~ (—(1 Н е + ^-Не ))J i (pr)rdr = — / / — JPrpJ(pr)rdrp 2 H e (p)p'dp ' + ∂r σ zz r ∂r                         σ zz

∞∞

+ / /( ЕГ — JJp^rPJJpP^rPr^rpH е (p ’ )pdp.

_{0 0} ∂r σ zz

Для кусочно-постоянной модели среды по радиальной координате с числом гра- ниц N ((N + 1)-ая граница находится меля, получим в бесконечности), используя интегралы Лом-

∞

У — J 1 (rpJ (pr)rdr

₀ zz

N i r k+

= $2 ~    ji(rp,)ji(pr)rdr k=1 σzz rk

и

∞

[ (- -

∂r σ zz

N1                         1

^)J i ⁽ rp ^)J 0 ⁽ pr ^)rdr = 5 jA—IJ i r k p ^)J 0 ⁽ pr k ^)r k , A— = σ z^kz                          σ z^kz

k=1

k +1 σ zz

-

k ^. σ zz

Таким же образом, используя преобразование Фурье – Бесселя первого порядка для второго и третьего уравнений, получим:

м N     r k + 1

д^Н е = — [E ^a rr [ Jprp'JpprpdpE r (p ' )pdp — J px ;

₀ k =1      _{r k}

F

E _r ∂z

Ж n      r k + 1

^- /[Ё a^k zz / ^J i ^(rp)J i ⁽ pr) ^rdr ]p ² He ^(p )p'dp ‘ +

I ^k=1    r k

∞ _N

+   £(a— ^)J i ^(r k p'Mpr k ^)r k pH o ⁽ p )pdp

0 k=1    ^a z^z

xH _e(p ’ )pdp + / — J Z^x J o (pr)prdr - σ zz

R s

OO n      r k+1

iu j^ V™ / Ji(rp)J1 (pr)rdr o k=1

r k iωB _θ ^ex ,

X

где R _s – радиус источника по радиальной координате;

( -p'r k+ Mfir k+1 'JWrk +1 ) + pr k+1 J 1 (pr k+1 )J o (pr k+1 )

+

r k + 1

У J1(rp’')J1(pr)rdr rk

^{p 2} - p²,

, pr k J 1 (pr k )J o (p r k ) - pr k J 1 (pr k )J o (pr k ) ‘ /

⁺               p ‘ ² - p 2                ^,p = ^

pr k+1 J 1 (pr k+1 ) ² - 2r k+1 J 1 (pr k+1 )J o (pr k+1 )+ pr k+1 J o (pr k+1 )

+

2p

-pr k J i (pr k ) ² + 2r k J^pV k )J o (pr k ) - pr k J o (pr k ) ²

- +

2p

,p ‘ = p

– есть интеграл Ломмеля [5].

В случае однородной среды, используя свойство

∞ f Jn(pr)Jn(p'r)rdr = 16(p - p’) = 16(p - p’), ρρ′

где p 5(p) - дельта-функция Дирака в цилиндрической системе координат, получим

∂

7T H O = ^{- a} rr E r ⁽ p) ∂z

ex

- J _r ,

^d F - Л ^E r ∂z

1            fl™,..,

(—p ² + '^P oo ) H q (p) +   —J_z J o (pr)prdr - v^Bq .

σ zz                         σ zz

R s

В противном случае, в случае радиально-неоднородного слоя, остаются формулы (1).

Для каждого слоя добавим и вычтем выражения, связанные с внешним бесконечным слоем с удельной электропроводностью σ _r ^N _r , σ _z ^N _z и магнитной проницаемостью ^µ θ^Nθ ^:

∂

7T- H O = ^- ∂z

“ N - 1

£<■*

o k-1

a N ) / J i (rp)J i (pr)rdr]E (p’)pdp - r k

a N E r (p)

- J rx   (2)

^d w

E _r ∂z

r k +1

-4) [ Mrpv^prydrwH о (p^p'd^ ^σ zz

7 N - 1 !

^- /i E⁽

σ

₀ k -1

∞ _N

+ [ ES^A~k^{J (r} k ^p)J 0 ⁽ pr k ^)r k pH 9 ^(p Wdp ' ^σ

₀ k-1

r k +1

-

r k

-

∞ _N

'^ [E^ ko ^- P No ) / ^JA^rp PAprJdrVJ о ⁽ p'ydp ' — (^p ² + iwp N ^)H о ⁽ p ^{) + σ}

0 k^-1

zz

r k

+ [ —jg^Jo^prdprdr σ zz

- iωB _θ ^ex .

R s

Для вертикальной составляющей вектора стороннего тока радиуса a найдем [6]:

a   aa

[ — Je^x J g (pr)prdr = —Jf? J Jo(ppprdr = -Jf^x- J Jp(pr)prdpr = — Jf^xaJ-^ap). σ                σ                   σ ρ               σ ρ

0                                          0                                   0

Функция Хевисайда в цилиндрической системе координат имеет вид Г U (r — a), поскольку 1 dr (r Г U(r — a)) = 1 5(r — a) - дельта-функция Дирака в цилиндрической системе координат.

Для J ex = I[U(z + Az) — U(z — Az)] 1 [U(r) — U(r — a)], где I - сила тока на токовом электроде, стекающего из электрода (либо втекающего в электрод) высотой 2Az s радиусом a , получим

∞∞

J re^x (z,p) = J J ex (r)rdr = I[U(z + Az) — U(z — Az)] J ^[U(r) — U(r — a)]J 1 (pr)rdrJ r ^ex 00

a

= I[U(z + Az) — U(z — Az)] / J ₁ (pr)rdr = —I[U(z + Az) — U(z — Az')]-(J ₀ (pa) — 1). ^ρ

Аналогично получим для B ^x , с учетом кольца с внутренним радиусом а ₀ и внешним радиусом a,

∞∞

_{B θ}ex

= У BJrdr = I[U(z + Az) — U(z — Az)] У r [U(r — o) — U(r — a)]J 1 (pr)rdrJ _r ^ex 00

a

= I[U(z + Az) — U(z — Az)] / J1(pr')rdr = —I[U(z + Az) — U(z — Az)]-(J0(pa) — J0(pa0)). ρ a0

Проведем интегрирование по центральной координате источника zg, и высоте ис- zo+Дza

- λ | - ^′ | _{dz .}

точника 2Az s функции f e z o - Дz _a

Для z > z ₀ + Az s ,

Z о + Д Zs у e-^z-Z о-Д s

' )d_z‘ — _____e^-^(z - z o )/ pyzsz.,

λ

-

e ^- УХд s ) ) = e

-V x(z - z o ) 2:sinh(VAAz s )

λ

.

Для z < zo — Azs, zo+Azs f ^X(z-z')^ ‘ _ 1    ^A(z-zo)/ -TAAzs _ TAAzs) _ TA(z-zo) 2 sinh(V AAzs)

• — \\                               )                     \A

z o - Az s

Для z ₀ + Az s > z > z ₀ — Az s ,

z

Ie zo -Azs

z o +Az s

:^-^ ^{( z - z, )} dz + у ^--^dz' = y = (2 — e-^ z - z ⁰^ ) z

- e v^(z z o Az s ) )

Отсюда, с учетом последних выражений, заменяя несобственные интегралы конечными суммами в уравнениях (2), получим систему уравнений вида d f [°] L12 A     Vext

S X - U1 [°]J X + Y ’ где X - (HO , He - He (z) и Er — Er (z) - вектор-столбцы, составленные из функций Hθ и Er для каждого значения ρ. Аналогично составляются векторы-столбцы для ([°] A                 (Jerxt\ вариантов в зависимости от типа источника Y — I jext ) , или Yext — I [°] I , или

Yext — | Pit! , или их комбинаций, [°] - нулевой вектор столбец соответствующей Bθ размерности.

Матрицы L ₁₂ и L ₂₁ - есть матрицы соответствующей размерности, зависящие от параметров модели, частоты и значения ρ.

Из последней системы уравнений, исключая вектор Er , получим систему для разных типов источников д2                            д2                    д      д2

H e ^— L 12 L 21 H 0 + L 12 JZ ’ Tf^H e ^— L 12 L 21 H 0 + ~ZT^Jr ’ TiH ^ ^— L 12 L 21 ^H e + L 12 B ’ дz ²                           дz ²                   дz     дz ²

решение которых имеет вид:

He — ve ^z Ci + ve-^z C2 + Hf, где A, (Re (А) > °) - собственные значения матрицы L12L21 — vAv-1, v - матрица, составленная из собственных векторов матрицы L12L21 соответствующих ее собственным значениям; Hf – первичное поле соответствующих источников ext ∂ ext        ext

L 12 J z ’ dz J r ’ L 12 B e ■

Удовлетворяя граничным условиям на границе раздела сред по координате z с номерами 1 и 2 вида [ H e ] — ° [L 1₂dz H 1 — L 1₂dz H 2 ] — °, найдем неизвестные вектора коэффициентов C^ C ₂ и, таким образом, решим прямую двумерную задачу для радиально-неоднородной горизонтально-слоистой модели среды. Используя уравнение E _z — Ay (1 dr (rH _e )) — у¹- J ex , найдем вертикальную составляющую электрического поля. Из уравнения dz H _e — —a _rr E r — Jex получим выражение для радиальной составляющей плотности электрического тока в спектральной области

J r — — . H e + J ex — — (vv^e ^^z C 1 — vv^e^- ^^z C 2 + . H f ) + J ^x .

∂z ^r                                        ∂z ^{θ r}

Следовательно, для нахождения компонент электромагнитного поля достаточно решения уравнения для азимутальной составляющей напряженности магнитного поля.

После нахождения неизвестных коэффициентов перейдем к нахождению полей. При этом учтем, что измерительные электроды и датчики имеют некоторый размер по вертикальной координате. Проинтегрируем найденные компоненты электромагнитного поля по вертикальной координате по отрезку длины 2Az - по высоте датчика.

z+∆z                                                                z+∆z

1 Г       ‘\ 7 ‘       Vxz sh(y^Az)           / г _г sh(\/XAz)         1 f , ‘

H ⁹ =2Az J H ^{( z ) dZ} = ^V e A -■ C 1 ^{+ V} e       \ ,- C 2 ⁺ 2A J H d ^Z '

z - ∆z                                                                       z - ∆z

2.    Алгоритм вычисления неизвестных коэффициентов

В каждом слое с координатами кровли Z k и подошвы Z k+1 (z k+_i > z > Z k ,k = 0, M, M +1 - количество слоев, включая верхнее и нижнее полупространства) решение для H θ может быть представлено в виде

H = Vke^zCki + Vke-^zCk,2 + Hf (z, z0) = = Vke (z-Zk+1)Ski + Vke^(z-zk)Sk,2 + Hf (z, zk), где Sk,i = ev^kZk+1 Ck,i, Sk,2 = e-^kzzkCk,2 - новое обозначение векторов неизвестных коэффициентов; Hkf(z,z0) - первичное поле источника в слое с номером k; zk+1 > z0k > zk .

Введенное переобозначение для неизвестных коэффициентов позволяет выразить решение в слое через убывающие экспоненты:

v o S o , i - V i e ^-/ ^ 1 ^{h 1} S i,i - V i S i,2 = H 1f (z i , z 0 ) - H f (z i ..-.

⁰ L

Xo S0,i — Li2Vi V^ie   x1h1 Si,i + L{2 Vi\/- i,2 =

1 ^∂   1 f 1      0 ^∂   0 f 0

= L i2 d_z H e ^{( z}l , ^z 0 )   L i2 d_z H e ^{( Z}l , ^Z 0 );

^V i S i,i ^{+ V}l^e ^h ¹ ' S i,2 ^{— V} 2 e ^hh S S 2,i — ^V 2 S 2,2 = H f ^{( z} 2 , Z 0 ) ^— H f ^{( z} 2 , ^z 0 );

^{L 1} 12 ^ν 1

λ 1 S

1 , 1

- L i2 V^e ^-      S i,2 - L 22 V 2 _хх 2     h ² S 2,i + L ² ₁₂ V 2 _V^/X2 S 2,2 =

2 ^∂   2 f 2      1 ^∂   1 f      1

= L i2 d_z H 9 ^(Z 2 , ^Z 0 )    L i2 d_z ^H 9 ^(Z 2 , ^Z 0 );

• ^VkSk,k^{+ V}k^e /^khk Sk,2 — ^Vk+i^eV^Ak+1^hk+1 Sk+i,i ^{- V}k+iSk+i,2 = = Hk^k+if(Zk+i, Zo^k+i) - Hf (Zk+i, Z0);

  k+i/7,  ^T           fk+i ^d k+f¹?

  ⁺Li2 ^Vk+rv ^Xk+i^Sk+i,2 = Li2 dZ^H_e

  
  
3.    Результаты компьютерного моделирования

Г k+i,, /Г" C^- V^ k+1^hk+1Q I L _i2 ^V k+rv ^X k+i e ^v S k+i,i + (Z k+i , Z o^{k +i} ) - L k 2^H f (z _k+ i ,z 0 );

T M         q      тМ    /Т ^-y^MhMQ     M+ +1      /\    Q

L 12 ^ν M λ M S M,1 ^- L 12 ^ν M λ M ^{e    M M} S M,2 ^- L 12 ^ν M+1 λ M+1 S M+1,2

M+1 ^∂   M+1f     M+1    M ^∂ Mf M

= L12  dz H3    (zM, z0   )   L12 dz H (zM, z0 ), где hk - толщина k-го слоя, k = 1, M.

Зная неизвестные коэффициенты, электромагнитное поле может быть найдено как на оси скважины, так и в околоскважинном пространстве.

Описанный выше метод вычисления программно реализован. Проведены вычислительные эксперименты для ряда практических геофизических примерных задач.

Пример 1. Низкочастотное приближение.

Для разработки геофизических снарядов с целью изучения околоскважинного пространства на низких частотах необходимо проведение численных экспериментов с целью определения параметров аппаратуры для решения геологических задач. Пусть скважина диаметром 0,1 м с удельной электропроводностью 0,1 См/м пересекает горизонтальный пласт (средний слой) метровой толщины с удельной электропроводностью 0,01 См/м (pис. 1). Области, находящиеся выше и ниже пласта, (верхний и нижние слои) имеют удельную электропроводность 1/30 См/м. Электромагнитное поле возбуждается источником частотой 100 Гц, находящимся в скважине на удалении 0,25 м выше верхней границы пласта. Геометрические размеры источника: радиус a=0,05 м, высота h=0,001 м. На рис. 2 представлены результаты решения прямой двумерной задачи на оси скважины для данной модели среды.

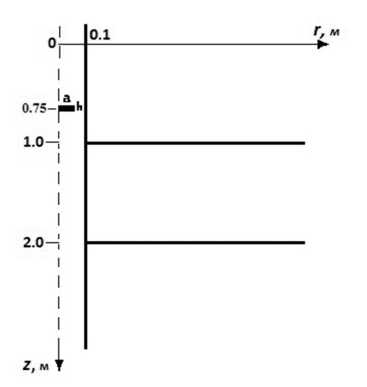
Рис. 1 . Модель среды – скважина пересекает пласт

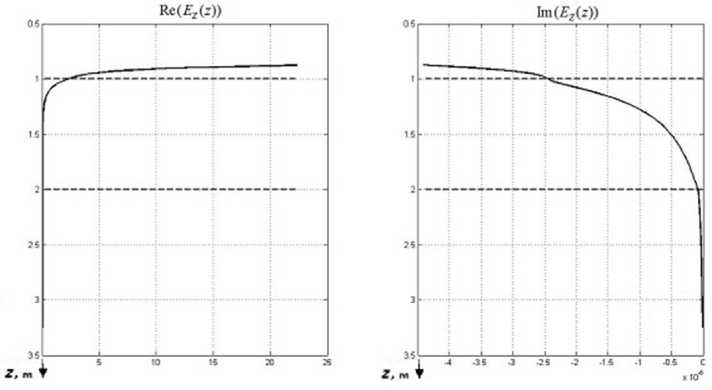
Рис. 2 . Действительная (a) и мнимая (б) части вертикальной компоненты напряженности электрического поля на оси скважины для частоты 100 Гц

Пример 2. Высокочастотное приближение (георадар) для горизонтально-слоистой модели геологической среды.

Одна из практических задач – поиск и разведка месторождений газогидратов. Газогидраты не выявляются с использованием стандартных методов исследования скважин. Однако известно, что они обладают различными диспергирующими свойствами удельной электропроводности по отношению к вмещающим породам [7]. Это требует разработки методических основ изучения таких объектов на основе высокочастотных методов геоэлектрики, каким является георадарный метод в скважинном варианте [8].

На основе предложенного похода к решению прямых задач в скважинном варианте разработанного программное обеспечения моделирования электромагнитных полей в высокочастотном приближении. Основная проблема – необходимость учета широкого диапазона пространственных частот, что реализовано на декадном разделении носителя подынтегральной быстроосциллирующей функции в обратном преобразовании Фурье – Бесселя и переходе к интегрированию с разным шагом на каждой декаде.

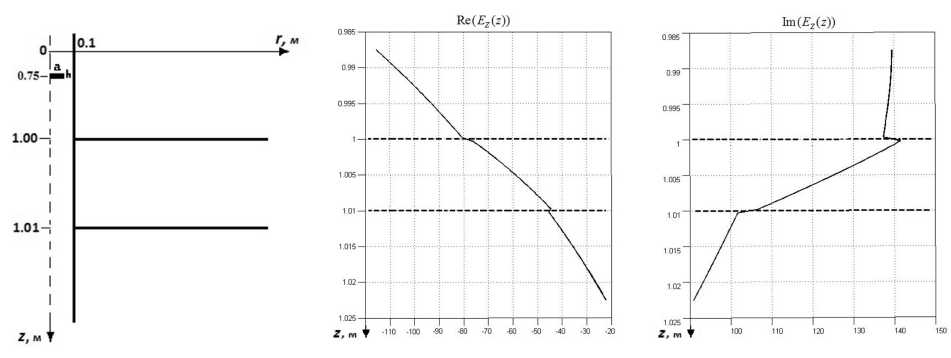
Рис. 3. Модель среды – сква- Рис. 4. Действительная (a) и мнимая (б) части вер-жина пересекает газогидрат- тикальной компоненты напряженности электрического ный пласт                поля на оси скважины для частоты 250 МГц без учета дисперсии диэлектрической проницаемости

Пусть скважина (рис. 3) диаметром 0,1 м с удельной электропроводностью a s = 0,1 + iu Юблу См/м пересекает горизонтальный пласт (средний слой) сантиметровой толщины. Области, находящиеся выше и ниже пласта, (верхний и нижние слои) имеют удельные электропроводности a 1 = a ₃ = 0, 01 + iu Югу См/м. Вертикальное электромагнитное поле с частотой 250 МГц возбуждается источником, находящимся в скважине на удалении 0,25 м выше верхней границы пласта. Геометрические размеры источника: радиус a=0,05 м, высота h=0,001 м.

Вычислительный эксперимент проведен для двух случаев удельной электропроводности газогидратного пласта: I) без учета дисперсии диэлектрической проницаемости (при a ₂ = 310 + iu Югу См/м), и II) с учетом дисперсии диэлектрической проницаемости (при a ₂ = зо^д^ХС^ См/м) - модель Cole-Cole [9].

Результаты расчетов для случая I представлены на рис. 4 – 6. Здесь на рис. 4 показана вариация вертикальной компоненты напряженности электрического поля вдоль оси скважины. Азимутальная компонента напряженности магнитного поля показана на оси скважины (рис. 5) и в плоскости 0 = const (рис. 6).

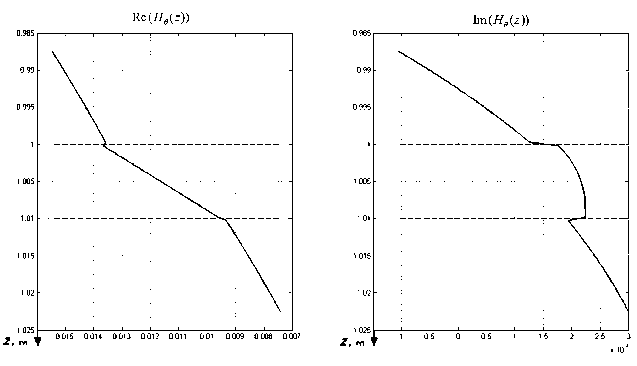
Рис. 5 . Действительная (a) и мнимая (б) части азимутальной компоненты напряженности магнитного поля на оси скважины для частоты 250 МГц без учета дисперсии диэлектрической проницаемости

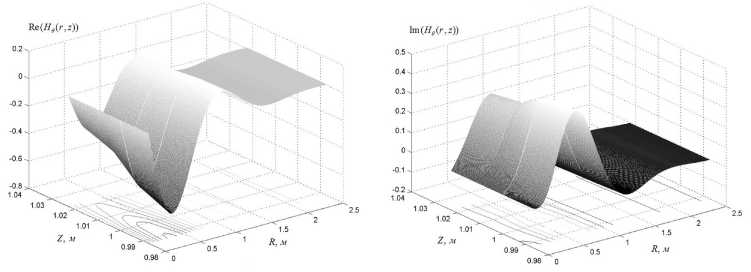
Рис. 6 . Действительная (a) и мнимая (б) части азимутальной компоненты напряженности магнитного поля в плоскости θ = const для частоты 250 МГц без учета дисперсии диэлектрической проницаемости

Учет диспергирующих свойств удельной электропроводности газогитратного пласта (вариант II) демонстрируется на рис. 7 – 9. Здесь на рис. 7 показана вариация вертикальной компоненты напряженности электрического поля вдоль оси скважины. Азимутальная компонента напряженности магнитного поля показана на оси скважины (рис. 8) и в плоскости θ = const (рис. 9).

Пример 3. Высокочастотное приближение (георадар) для радиально-неоднородной горизонтально-слоистой модели геологической среды.

Рассмотрим скважину диаметром 0,1 м с удельной электропроводностью и магнитной проницаемостью бурового раствора в ней соответственно σ _s = 0, 1 + iωε 0 80 См/м и µ _s = 10µ 0 , где µ 0 – магнитная проницаемость вакуума. Скважина имеет электрически слабопроницаемую глинистую корку (r _g = 0, 105 м) с параметрами См/м и σ _g = 0, 00001 + iωε 0 См/м и µ _g = µ 0 , и пересекает горизонтально-слоистую трехслойную среду. Горизонтальный пласт (средний слой) имеет толщину 10 см с электромагнитными характеристиками σ ₂₂ = 0, 01 + iωε 0 См/м и µ ₂₂ = µ 0 . Области,

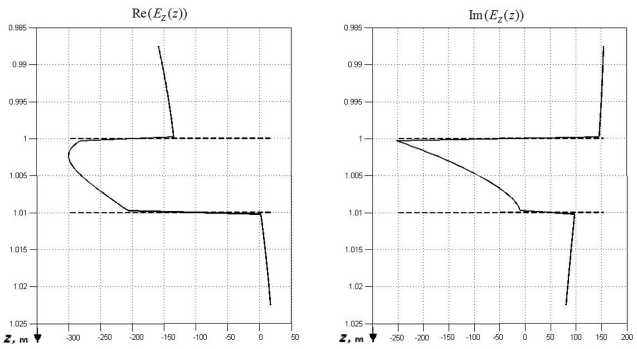
Рис. 7 . Действительная (a) и мнимая (б) части вертикальной компоненты напряженности электрического поля на оси скважины для частоты 250 МГц с учетом дисперсии диэлектрической проницаемости

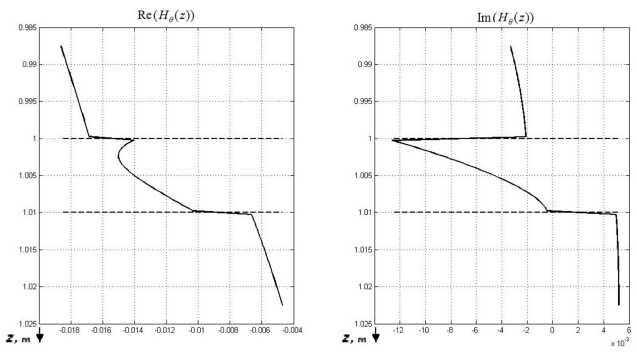
Рис. 8. Действительная (a) и мнимая (б) части азимутальной компоненты напряженности магнитного поля на оси скважины для частоты 250 МГц с учетом дисперсии диэлектрической проницаемости находящиеся выше и ниже пласта, (верхний и нижний слои) имеют одинаковые характеристики а12 = а32 = 0, 001 + iш£0 См/м и ^12 = ^32 = ^0 .В каждом горизонтальном слое фильтрат бурового раствора образует зоны проникновения (рис. 10) радиусы внешних границ которых соответственно r1 = 0, 395 м, r2 = 0,145 ми r3 = 0, 045 м. Электрические и магнитные свойства зон проникновения первого и третьего слоя одинаковы - ац = а31 = 0, 01 + i^e0 См/м и ^11 = ^31 = ^0. Зона проникновения фильтрата бурового раствора второго слоя задана следующими параметрами: ^21 = 30 + гшво См/м, ^21 = ^0•

Вертикальное электромагнитное поле с частотой 250 МГц возбуждается источником, находящимся в скважине на удалении 0,25 м выше верхней границы второго слоя (пласта). Геометрические размеры источника: радиус a=0,05 м, высота h=0,001 м.

Результаты вычислительного эксперимента для примера 3 представлены на рис. 11 – 13. Здесь на рис. 11 показана вариация вертикальной компоненты напря-

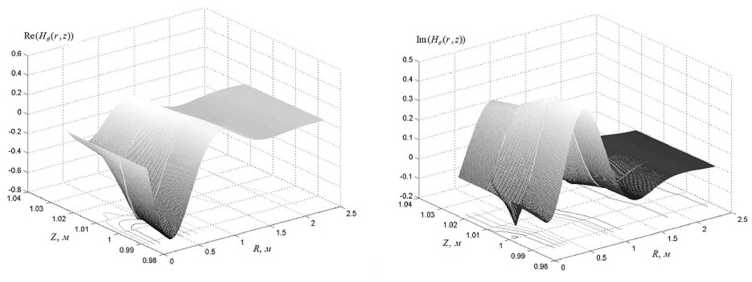
Рис. 9 . Действительная (a) и мнимая (б) части азимутальной компоненты напряженности магнитного поля в плоскости θ = const для частоты 250 МГц с учетом дисперсии диэлектрической проницаемости

женности электрического поля вдоль оси скважины. Азимутальная компонента напряженности магнитного поля показана на оси скважины (рис. 12) и в плоскости θ = const (рис. 13).

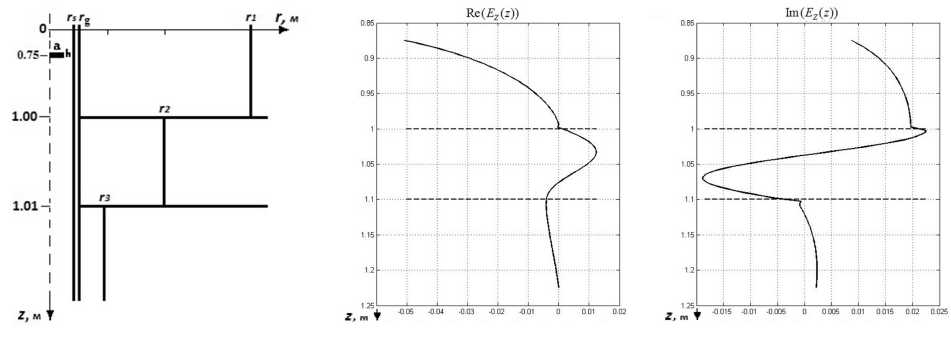
Рис. 11 . Действительная (a) и мнимая (б) части вертикальной компоненты напряженности электрического поля на оси скважины для частоты 250 МГц

Рис. 10 . Модель горизонтально-слоистой радиальнонеоднородной среды

Заключение

Сведение системы уравнений Максвелла к системам обыкновенных дифференциальных уравнений позволяет использовать интегралы Ломмеля, которые в свою очередь создают возможность получить аналитические выражения для некоторых интегралов.

Учет пространственных размеров приемников и источников приближает решение к реальным системам наблюдения. Учет пространственных размеров источников позволяет исключить сингулярности и вычислить поле внутри источников, что является актуальной задачей исследования согласования источника и нагрузки.

Полученное решение позволяет находить электромагнитное поле во временной области, используя обратное преобразование Фурье. Это создает теоретическую основу

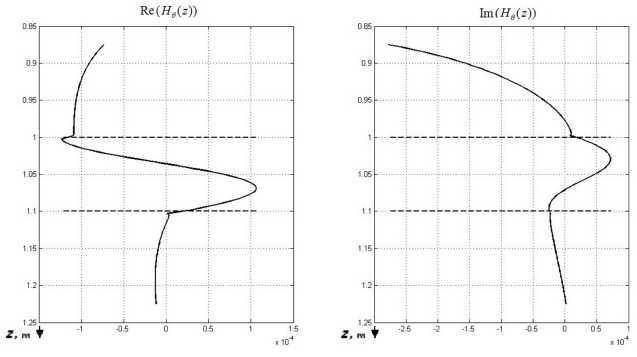
Рис. 12 . Действительная (a) и мнимая (б) части азимутальной компоненты напряженности магнитного поля на оси скважины для частоты 250 МГц

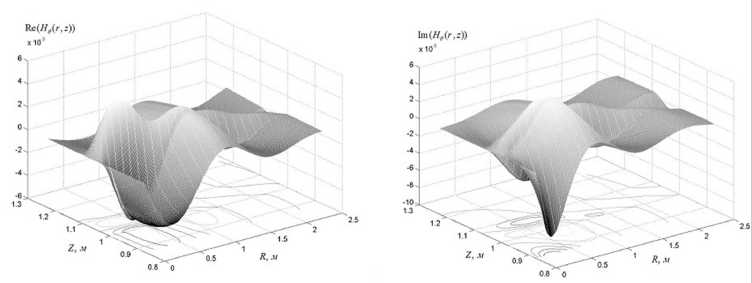
Рис. 13. Действительная (a) и мнимая (б) части азимутальной компоненты напряженности магнитного поля в плоскости θ = const для частоты 250 МГц разработки геордарной технологии в скважинном варианте по обнаружению тонких слоев, обладающих дисперсией удельной электропроводности.