Моделирование процесса деформирования и разрушения образцов соляных пород при сжатии

Стандартные испытания на сжатие образцов цилиндрической формы с различным отношением высоты образца h к его диаметру d при постоянной скорости перемещения траверсы пресса широко применяются для различных соляных пород. Характер разрушения образцов различной высоты h/d при сжатии обусловлен видом напряженного состояния [1, 2], зависящим от краевых эффектов контактной поверхности образца с траверсой испытательной машины и наличием трения [3, 4].

Предел прочности образца при сжатии определяется как отношение максимального усилия к начальной площади образца и суще-

ственно зависит от относительной высоты образца h/d . Этот эффект, объясняемый влиянием краевых эффектов на торцах образца, в инженерных соотношениях учитывается путем введения, так называемого, коэффициента формы [5, 6].

Известно, например [5, 6], что как в режиме активного нагружения, так и в режиме ползучести, соляные породы деформируются с образованием множественных микродефектов (микротрещин). Поэтому критерий прочности (потери несущей способности) соляных пород должен основываться на величине накопленной поврежденности в ходе неупругого деформирования.

Модели материалов, учитывающие рост поврежденности в процессе нагружения, яв- ляются достаточно сложными [6–8], содержащими дополнительные параметры, и требующими экспериментального определения. Поэтому для практических расчетов в более простом варианте подобный критерий может использовать вместо параметра поврежденно-сти накопленную деформацию.

Понятие предельной деформации (и критериев на ее основе) широко применяется в инженерных оценках времени устойчивого состояния целиков и кровли выработок соляных пород [9], оценки сохранения сплошности слоев водозащитной толщи [10]. Так, инженерный критерий предельной деформации сжатия как функции коэффициента формы [9] применяется при оценке перехода целиков соляных пород из стадии стационарной в стадию прогрессирующей ползучести.

В работе [11] представлен новый критерий деформационного разрушения соляных пород, представляющий модификацию известного критерия разрушения металлов [12], в виде главной деформации, ограниченной предельным значением, зависящим от коэффициента жесткости напряженного состояния (отношения гидростатического давления к интенсивности напряжений). Определены вид зависимости и параметры критерия разрушения для образцов пород сильвинита и карналлита Верхнекамского месторождения при статическом нагружении.

Данная работа посвящена развитию критерия разрушения деформационного типа для соляных пород [11], математическому моделированию экспериментов по активному сжатию образцов сильвинита в 3D-постановке, в том числе с наличием глинистых прослоев. Показано, что предлагаемая модель описывает кривую напряжение-деформация при сжатии, зависящую от относительной высоты образца, включая ниспадающую ветвь.

Формулировка критерия разрушения

Известно, что соляные породы проявляют в некоторых случаях вязкопластические свойства, а в некоторых – хрупкие, в зависимости от характера напряженного состояния [13]. Учитывая этот фактор, был сформулирован деформационный критерий разрушения соляных пород [11] в следующем общем виде:

t

J t0

dε ₁

^ 1 пр ( k , д , ё u , W )

< 1,

где ε ₁ ^пр – предельная главная деформация, зависящая от коэффициента жесткости напряженного состояния k , температуры θ , скорости деформирования ё_u и влажности W ;

ε ₁ – накопленная главная деформация.

Коэффициент жесткости напряженного состояния определяется как отношение первого и второго инварианта тензора напряжения: ^k = Р / ^O u ,                (2)

где p = (1/З) ^^^^ - среднее (гидростатическое ) давление, o u = ( (3/2) S j S j )^{1 /2} - интенсивность напряжений; S _ij = o _ij - p S _ij - компоненты девиатора тензора напряжений; ё _и = ((2/3) ee _у)^1/2 – интенсивность скоростей деформаций; e ij - компоненты девиатора тензора скорости деформаций.

Непосредственное использование критерия (1) в практических расчетах предполагает его значительное упрощение:

– не будем учитывать в данной статье зависимость предельной главной деформации ε ₁ ^пр от температуры, скорости деформирования и влажности в силу практического отсутствия исходных данных;

– от интеграла (1) перейдем к конечной зависимости.

Таким образом, следуя [11], предлагается использовать упрощенный вариант критерия (1) в виде

ё 1 <  ё П ( к ) .                   (3)

Зависимость ε ₁ ^пр ( k ) была установлена в [11] путем численного моделирования процесса сжатия образцов соляных пород различной геометрии, и последующего усреднения полей напряжений и деформаций.

Зависимость ε ₁ ^пр ( k ) выражается в виде двух ветвей (в положительной и отрицательной области параметра k ) как

ё 1 >  ё п ( p / o u ) = к_М -( 0,012 к ² + 0,136 к + 0,50 ) при k < 0,

^ё 1 >  ^ё п ⁽ Р / °_и ) =

= к_М • ( 9,13 к ³ -1,63 к ² + 1,77 к + 0,50 )

при k > 0,             (4)

где k_М = 2,1 (для сильвинита); k_М = 0,45 (для карналлита).

Отметим, что, согласно принятому правилу знаков напряжений в геомеханике, вариант k < 0 соответствует растяжению, а k > 0 – сжатию.

По аналогии с классическими критериями разрушения введен коэффициент запаса прочности по деформационному критерию:

n ₌ ε 1 ^пр ( p / σ u ) ε ₁

.

Учет влияния уровня поврежденности на механические характеристики

Параметры критерия k_М и сам вид зависимости (4) определены так, что условие n < 1 означает фрагментацию области (расчетной ячейки), где оно выполняется, а условие 1< n – наличие некоторой поврежденности.

Рост поврежденности в некоторой локальной области ведет, как правило, к изменению механических характеристик – уменьшению модуля упругости, предела текучести и прочности. Моделирование процессов деформирования и разрушения материалов, в том числе соляных пород, должно учитывать ослабление механических свойств расчетного объекта в ходе процесса нагружения.

В качестве параметра поврежденности ω в данной модели выступает величина, обратная коэффициенту запаса прочности:

ω = ¹ =      ^ε 1      .             (6)

n ε ₁ ^пр ( p / σ_u )

В модели разрушения в поврежденных областях для модуля упругости, предела текучести и прочности используется коэффициент снижения механических свойств L s :

L s = 0,2–0,5 для n < 1 ( ω > 1),

L s = 0,75 для 1 <  n < 2 (0,5 <  ω < 1), (7)

L s = 0,85 для 2 <  n < 3 (0,5 <  ω < 1).

При выполнении условия 3 <  n ( ω < 0,33) характеристики соответствуют исходному материалу.

Алгоритм учета поврежденности при расчете деформирования и разрушения материалов в пакете ASNSYS

Для учета уменьшения механических характеристик при трещинообразовании в ходе решения задачи в пакете ANSYS был разработан и реализован следующий алгоритм:

• 1)    Проверка критерия прочности . Запускается вложенный цикл, который проверяет выполнение деформационного критерия для всех конечных элементов на каждом шаге нагружения. Вычисляется коэффициент жесткости напряженного состояния (2), а на его основе – значение коэффициента запаса прочности. (4). Если для коэффициента запаса (уровня поврежденности) выполняются какие-либо из условий (7), то исходный материал элемента заменяется соответствующим поврежденным (с ослабленными механическими характеристиками) материалом со своим номером. Обратная замена (улучшение механических характеристик) невозможна. В конце каждого цикла нагружения запоминается тип (номер) материала (исходный или поврежденный, соответствующий условиям (7)) для каждого элемента.

• 2)    Визуализация . Для отображения коэффициента запаса прочности была написана вспомогательная процедура. Чтобы получить изображение поврежденной зоны на определенном шаге формируется массив с номерами элементов и соответствующими типами (номерами) материалов элементов для данного шага. После завершения расчета поврежденные зоны на нужном шаге нагружения изображаются с помощью встроенных функций.

Моделирование ниспадающей части диаграммы напряжение-деформация при сжатии образцов различной относительной высоты

Проведено численное 3D-моделиро-вание в пакете ANSYS экспериментов по сжатию образцов сильвинита и карналлита различной геометрии: h/d = 0,5; 1; 2.

В силу симметрии рассматривалась четверть образца, на плоскостях разреза формулировались условия симметрии, на нижнем торце – полное прилипание, на верхнем торце по шагам задавались осевое перемещение и условия отсутствия перемещений в плоскости торца. Установлено, что принятые граничные условия соответствуют наличию сильного трения на контактной поверхности образца и траверсы испытательной машины.

В качестве физических уравнений ис- пользована модель изотропного мультили-нейного деформационного упрочнения. В этой модели использованы экспериментально полученные кривые [9] напряжение-деформация для высоких образцов (h/d = 2), где реализуется напряженное состояние, близкое к одноосному напряжению.

В качестве примера на рис. 1 показаны фрагменты высоких образцов с полем коэффициента запаса прочности при различной осевой деформации сжатия (темно-синим цветом показана фрагментированная область с n < 1). Видно, что даже в случае высокого об- разца напряженное

состояние отличается от

одноосного.

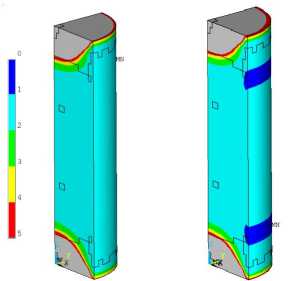
а – ε y = 2,0 %;   б – 2,2 %;

Рис. 1. Поля коэффициента запаса прочности n при сжатии высокого (h/d = 2) образца для различной деформации сжа-

в

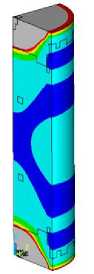
в – 2,4 %

тия

Была проведена серия расчетов для образцов различной геометрии, на основании которых построены расчетные диаграммы напряжение-деформация.

Осевая деформация задавалась по шагам в виде кинематического граничного условия (это соответствует реальному эксперименту, в котором задавалась постоянная скорость сжатия 1 мм/мин).

На каждом этапе деформирования определялись осевые напряжения σ_z во всех элементах на торце образца и суммарное усилие сжатия

P z = J " dS .

S

На рис. 2 показаны кривые напряжение-деформация, включающие ниспадающие ветви диаграммы, полученные расчетным путем для образцов различной геометрии. Верхние кривые на рис. 2 получены для низких образцов h/d = 0,5, а нижние – для средних h/d = 1 и высоких h/d = 2.

Подчеркнем, что ниспадающие ветви диаграмм деформирования не задавались изначально, а были получены путем численного моделирования процесса разрушения образцов.

Кроме того, для образцов всех размеров использована одна и та же диаграмма изотропного мультилинейного деформационного упрочнения.

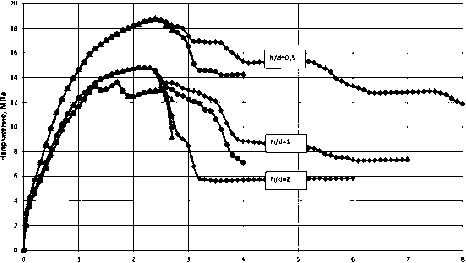
Рис. 2. Диаграммы деформирования образцов различной геометрии, полученные расчетным путем

Отметим, что предложенная модель, включающая деформационный критерий разрушения, качественно описывает экспериментально наблюдаемый эффект повышения предела прочности и увеличения средней предельной деформации разрушения при уменьшении относительной высоты образца [1–3, 6, 8].

3D-моделирование экспериментов по сжатию образцов соляных пород с глинистыми прослоями

На практике при испытании образцов соляных пород часто приходится иметь дело с образцами, имеющими различные включения гли- ны и других минералов. Эти включения иногда носят характер прослоев, расположенных преимущественно в меридиональном или широтном направлениях относительно оси образца.

Поскольку пласты соляных пород имеют, как правило, сублатеральную структуру, то при извлечении керна для изготовления образцов из скважины, пробуренной вертикально, образцы будут иметь поперечные глинистые прослои. Для горизонтальных скважин образцы могут иметь продольные глинистые прослои.

Также была проведена серия расчетов по сжатию образцов, содержащих модельные глинистые прослои, расположенные вдоль и поперек образца.

Показано, что наличие глинистых прослоев может значительно изменить характер разрушения образца и повлиять на измеряемые механические характеристики. Это объясняется, прежде всего, тем, что глинистые прослои имеют механические свойства значительно меньшие (примерно, в 5–10 раз), чем свойства сильвинита или каменной соли.

На рис. 3 показаны области разрушения (поле коэффициента запаса n ) для высоких образцов с вертикальными (а) и горизонтальными (б, в) глинистыми прослоями.

а                 б         в

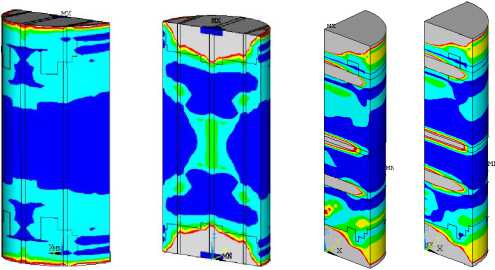
а – ε y = 2,6 %; б – ε y = 2,2 %; в – ε y = 2,4 %;

Рис. 3. Поля коэффициента запаса прочности n при сжатии высоких (h/d = 2) образцов при различном расположении глинистых прослоев

В обоих вариантах образцы содержали по три глинистых прослоя одинаковой толщины. В случае вертикальных прослоев необходимыми требованиями симметрии обладает половина цилиндрического образца (рис. 3, а).

Результаты расчетов (рис. 3) показывают, что области разрушения при поперечном расположении глинистых прослоев более критичны для потери несущей способности образца даже при меньшей осевой деформации (2,2–2,4 %), чем при продольном расположении (2,6 %).

Это объясняется тем, что горизонтальные прослои сильно деформируются по краям цилиндра, оставаясь менее сжатыми в центральной его части. Это приводит к изгибу основных слоев образца, способствуя их более интенсивному разрушению.

При дальнейшем сжатии образца разрушаются в основном прослои, основные слои при этом деформируются как жесткое целое.

На рис. 4 показано векторное поле перемещений высокого образца с горизонтальными прослоями. Значительное радиальное расширение образца наблюдается в месте расположения глинистых прослоев.

Анализ проведенных расчетов по влиянию глинистых прослоев позволяет сделать следующие выводы:

• –    разрушение образцов начинается с ослабленных глинистых прослоев, особенно это проявляется для высоких образцов;

• –    горизонтальные прослои начинают разрушаться раньше, чем вертикальные, оказывая более значительное влияние на прочность образца;

• –    глинистые прослои в низких образцах оказывают меньшее влияние на их прочность, чем для высоких образцов;

• –    наличие любых глинистых прослоев должно учитываться при экспериментальной оценке прочности соляных пород.

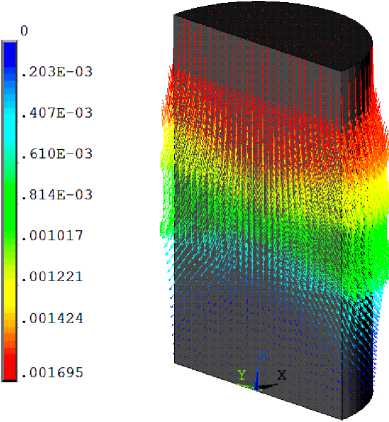
Рис. 4. Векторное поле перемещений ( ε y = 2,6 %)

Заключение

Представлена модель деформирования и разрушения соляных пород, основанная на модернизированном критерии деформационного разрушения, учитывающая изменение механических характеристик материала в зависимости от уровня накопленной повреж-денности.

Выполнен анализ характера разрушения образцов соляных пород различной геометрии, получены расчетные кривые напряжение-деформация при сжатии образцов, включающие ниспадающую ветвь диаграммы.

Численно смоделирован эффект увеличения предела прочности образца с уменьшением его относительной высоты, подтверждаемый экспериментально.

Изучен эффект влияния продольных и поперечных прослоев глины в образцах различной геометрии на характер разрушения при сжатии.

Показано, что наибольшее влияние имеют поперечные прослои глины в высоких образцах, обычно применяемых при стандартных испытаниях на сжатие. Влияние глинистых прослоев на разрушение низких образцов не столь существенно.

Авторы выражают искреннюю благодарность д.т.н. О.Ю. Сметанникову за консультации по вопросам программирования на языке APDL в программной среде ANSYS.