Моделирование процессов вакуумной сушки меда

Введение. Полезные свойства меда известны [1–3]. Высушенный мед используется в различных пищевых технологиях. Сушка меда имеет цель сохранения нативных свойств и полезных составляющих. Однако мед является термолабильным продуктом, что требует изыскания высокоэффективных способов сушки, которые позволят сохранить все свойства меда, которыми он обладал до высушивания. В связи с чем научная проблематика заключается анализе и совершенствовании способов и устройств сушки меда, обеспечивающих сохранение их ценных свойств.

Целью исследования [4] является изучение кинетики сушки высушенного в вакууме и сублимированного пчелиного меда, полученного из двух различных сортов: подсолнечный мед ( Helianthus Annuus L.) и акациевый мед ( Robinia pseudo acacia L.). Сушка в вакууме проводилась при начальной температуре образцов меда 25 °C, –20 и –40 °C. В образцах свежего и сушеного меда определяли содержание воды, общее количество растворимых сухих веществ, а также активность воды. Сублимационная сушка пчелиного меда при начальной температуре образца –40 °C привела к сокращению времени высыхания, влажности, активности воды и эффективному коэффициенту диффузии влаги.

Применена предварительная обработка.

В качестве потенциального метода получения высококачественного сухого меда была исследована микроволново-вакуумная сушка (MWV) [5]. Жидкий мед нагревали и обезвоживали в сушилке MWV до влажности менее 2,5 % в течение примерно 10 мин. Кривые сушки и изменения температуры образцов были протестированы во время MWV-сушки при различной мощности микроволнового излучения, уровнях вакуумного давления и толщине образцов. Содержание фруктозы, глюкозы, мальтозы и сахарозы в жидком и сухом меде определяли методом высокоэффективной жидкостной хроматографии (ВЭЖХ). Летучие вещества в жидком и сухом меде концентрировали методом твердофазной микроэкстракции (ТФМЭ), разделяли и идентифицировали методом газовой хроматографии-масс–спектрометрии (ГХ–МС). Толщина образца менее 8 мм и вакуумное давление 30 мбар были определены в качестве наилучших параметров для сушки методом MWV. Температура сердцевины образца была примерно такой же, как и температура поверхности, изменения температуры составляли от 30 до 50 °C при более высокой скорости обезвоживания, в то время как при сушке MWV потемнение меда не происходило. После сушки MWV в меде не наблюдалось существенных изменений в содержании фруктозы, глюкозы, мальтозы и сахарозы. Летучие кислоты, спирты, альдегиды и сложные эфиры составляли основную часть идентифицированных ароматических соединений использованного жидкого меда, а содержание спиртов и сложных эфиров изменялось незначительно. Содержание кислот заметно снизилось, в то время как содержание альдегидов и кетонов заметно возросло в меде, обезвоженном методом MWV-сушки [5].

В [6, 7] непосредственно процесс сушки осуществляется в вакуумной сушильной камере (ВСК). Длина ВСК около 530 мм, диаметр ВСК – 290 мм. Продукт в камере укладывался на специальный поддон, установленный на датчик массы. Объем лабораторной ВКС невелик, всего 0,035 м³. Были подобраны условия (остаточное давление P , тепловой поток Q , толщина слоя меда d , температура воздуха в камере T ), обеспечивающие высокое качество конечного продукта. Кроме того, было исследовано влияние указанных условий на энергетические затраты при вакуумной сушке меда с инфракрасными лампами (ВИКС).

В [8] было проведено сравнение ВИКС меда при разном подводе тепла. Проведена органолептическая оценка обезвоженных продуктов, а также оценены энергозатраты при использовании импульсного и ступенчатого способа подвода теплоты. Применение импульсного способа подвода теплоты позволяет на 1–2 балла повысить органолептическую оценку и снизить энергозатраты на 7–12 %. Сделан вывод, что импульсный способ подвода теплоты при вакуумной сушке меда является более предпочтительным.

Результаты [6–8] были получены на лабораторной установке с малым объемом ВКС и сравнительно небольшой массой загружаемого объекта сушки. Поэтому интенсивность испарения при сушке (ИИС) меда практически не оказывала влияния на протекание газодинамических процессов. В производственных условиях в ВСК большого объема может загружаться достаточно большая масса меда M0. Как было показано в [9], чем больше M0, тем большее влияние ИИС оказывает на газодинамические процессы в ВКС. Давление в ВКС может заметно возрасти, а время сушки – увеличиться.

Методика [9] была разработана на примере ВИКС сыра. Для ее применения при сушке меда необходимо получить аналитические зависимости ИИС от условий в ВСК. Этому посвящена данная статья.

Цель исследования – изучение влияния условий в вакуумной сушильной камере на интенсивность испарения при вакуумной сушке меда.

Задачи: получить зависимость интенсивности испарения при сушке меда от времени; рассчитать максимальные значения интенсивности испарения при изменении теплового потока, толщины слоя, остаточного давления.

Материалы и методы. Исходными данными послужили результаты экспериментальных исследований [6, 7]. В таблице 1 Wk – влагосо-держание меда в конце сушки, tk – время сушки. В [6] лишь указано, что при изменении теплового потока с 2 до 10 кВт/м² значение Wk возросло с 4,5 до 5 % (это строки 1 и 5 в табл. 1). Поэтому значения Wk в строках 2–4 – приближенные. В [7] не приведены конкретные значения Wk . Указано начальное влагосодержание W 0 = 21,5 %, а про конечное сказано «около 5 %», что и приведено в таблице 2 (строки 11–18). Значения времени сушки в строках 15–18 – приближенные, так как сняты с графической зависимости.

Таблица 1

Номер опыта	q	P	T	d	Wk	tk
	кВт/м2	кПа	°C	мм	%	мин
1	2	4	40	10	4,5	270
2	4	4	40	10	≈4,6	240
3	6	4	40	10	≈4,7	225
4	8	4	40	10	≈4,8	210
5	10	4	40	10	5,0	195
6	4	4	40	5	4,3	180
7	4	4	40	10	4,6	240
8	4	4	40	15	4,9	275
9	4	4	40	20	5,4	300

Данные опытов ВИКС меда [6]

Data from the VICS experiments on honey [6]

Данные опытов ВИКС меда [7]

Data from the VICS experiments on honey [7]

Таблица 2

Номер q P T d Wk tk опыта кВт/м2 кПа °C мм % мин 10 6 2 40 10 около 5 230 11 6 3 40 10 -- 245 12 6 4 40 10 -- 260 13 6 5 40 10 -- 275 14 6 6 40 10 -- 285 15 4 4 30 10 -- ≈295 16 4 4 40 10 -- ≈252 17 4 4 50 10 -- ≈192 18 4 4 60 10 -- ≈156 dm dt .

Обратим внимание, что условия проведения двух опытов в таблицах 1 и 2 указаны одинаковыми (опыт № 2 из [6] и № 12 из [7]). Установка для ВИКС использовалась одна и та же. Однако во втором случае больше как время сушки (на 35 мин), так и конечная влажность (примерно на 0,3–0,4 %). Но при одинаковых условиях увеличение tk должно приводить к уменьшению Wk . Остается предположить, что были изменены условия, не указанные в таблицах 1, 2. Действительно, в качестве объекта сушки в обеих статьях указан мед натуральный гречишный. Но в [7] указан и год сбора меда – 2019. Тогда как статья [6] была опубликована в 2018 г. Скорее всего, такая разница tk получилась из-за изменения свойств меда. Следовательно, верификацию математической модели необходимо проводить отдельно для данных опытов из таблицы 1 и таблицы 2.

Исходными данными также послужили графики динамики изменения ИИС J ( t ) (переведем единицы измерения J из %/час в %/мин) и относительной массы меда m ( t ) из [6]. Заметим, что на графике m ( t ) (рис. 2 из [6]) отсутствуют числовые значения на оси ординат m . Понятно, что m 0 = 100 %. Конечные значения пришлось восстанавливать по формуле (1). Например, при W k = 4,5 % m k = 86,0 %.

mk

= 100 •

100 + W_k

100 + W_o

ИИС (%/мин) представляет собой производную относительной массы по времени

В данной статье воспользуемся безразмерными переменными времени и ИИС

τ = t / tk , j = J/Jm ,                  (3)

где Jm – наибольшее значение ИИС при рассматриваемых условиях конкретного опыта.

Как правило, при аппроксимации кривых сушки за основу принимают экспериментальную зависимость m ( t ), а J ( t ) находят как производную по формуле (2) [10, 11]. Однако известно, что все методы численного дифференцирования являются неустойчивыми из-за случайных погрешностей измерений [12]. В данной статье за основу принята зависимость J ( t ), для нахождения m ( t ) используется численное интегрирование. Сушку делят на три этапа (см., например, [13, 14]). Экспериментальные точки [6], использованные на рисунке 1, показывают на отсутствие сколько-нибудь продолжительного периода с J = const; функция j (τ) возрастает по времени, достигает максимума Jm ( j = 1) и затем становится убывающей. Поэтому целесообразно аппроксимировать зависимость ИИС меда от времени многочленом n -го порядка j ≡ φn(τ)

φn(τ) = b 0 + b 1 τ + b 2· τ2 + … + b n · τn, (4) где b 0, b 1, …, b n – эмпирические константы, подлежащие определению по результатам экспериментов.

Тогда размерная функция ИИС выражается через безразмерную следующим образом:

J ( t ) = Jm · φn( t / tk ).

Запишем интегральное условие t_k

A m = j J ( t ) dt , A m = 100 - m k ,    (6)

где Δ m – изменение относительной массы за время сушки.

Максимальное размерное значение ИИС найдем, используя (5) и (6)

J m =7 m ^, I = 1 ^Ф n ^(T) d ^T .       (7)

t k ■ I          0

Проверку правильности подбора аппроксимации J(t) выполним путем сравнения экспериментальных значений me и результатов расчета по формуле t.    (t у mp (t ) = 100 - Jm '(ф n 7 dt .     (8)

• 0     V t k J

Для возможности оценки максимальных значений ИИС при различных условиях, как в [15], введем безразмерные величины теплового потока, толщины слоя, остаточного давления, где в качестве характерных величин используем следующие значения: Q* = кВт/м2; d* = 10 мм; P* = 4 кПа; T* = 40 °C.

Результаты и их обсуждение. На рисунке 1 представлено сравнение результатов расчетов по формуле (4) при n = 5 c экспериментальными значениями ИИС. Если увеличивать порядок многочлена, то согласие точек и линий улучшается незначительно. При n = 4 это согласие заметно ухудшается. В [6] отмечено, что значения времени сушки найдены со средним квадратичным отклонением (СКО) 10 минут, что составляет не более 5 % от tk . Линии 4 и 5 на рисунке 1 построены исходя из указанного значения СКО. Линия 3 построена по формуле (4), причем коэффициенты в указанной формуле найдены методом наименьших квадратов по всему массиву экспериментальных точек [6]. Видно, что эти точки находятся внутри обозначенного коридора. Следовательно, можно считать, что динамика ИСС в исследованных условиях может быть аппроксимирована в безразмерных переменных одной функцией φn(τ) с погрешностью, не превышающей СКО экспери-

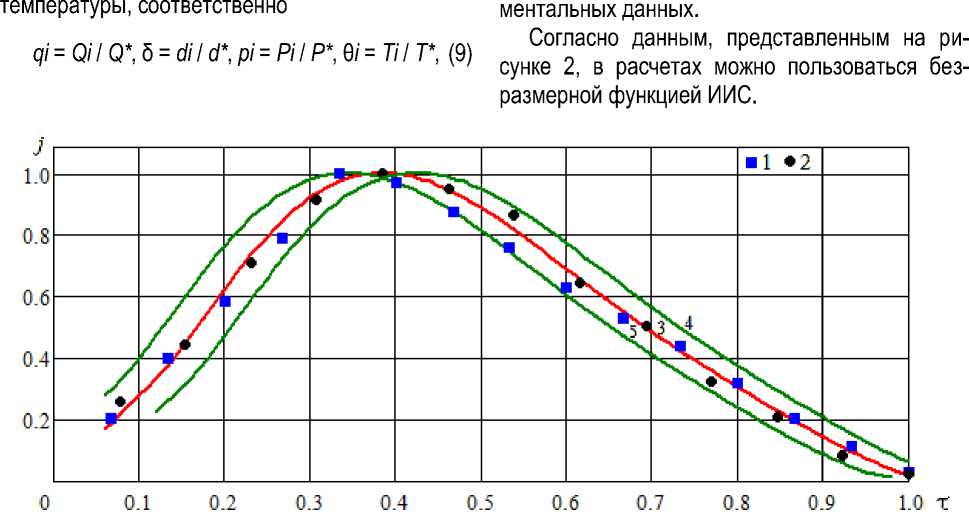
Рис. 1. Динамика изменения интенсивности испарения при сушке меда в безразмерных переменных (точки – экспериментальные данные [6]: 1 – Q = 6 кВт/м2; 2 – Q = 10 кВт/м2; линии – результат расчета: 3 – аппроксимация массива экспериментальных точек по формуле (4); 4, 5 – границы по СКО безразмерного времени)

Dynamics of change in evaporation intensity during honey drying in dimensionless variables (points – experimental data [6]: 1 – Q = 6 kW/m2; 2 – Q = 10 kW/m2; lines – calculation result:

3 – approximation of the array of experimental points according to formula (4); 4, 5 – boundaries according to the standard deviation of dimensionless time)

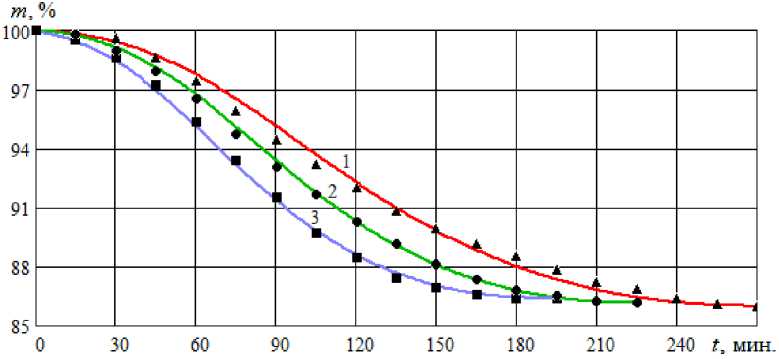
Рис. 2. Динамика изменения относительной массы меда при вакуумной сушке:

1 – Q = 2 кВт/м2; 2 – Q = 4 кВт/м2; 3 – Q = 10 кВт/м2

(точки – экспериментальные данные [6]; линии – результат расчета по формуле (8)) Dynamics of change in relative mass of honey during vacuum drying: 1 – Q = 2 kW/m2;

2 – Q = 4 kW/m2; 3 – Q = 10 kW/m2 (points – experimental data [6]; lines – calculations accordingto the formula (8)

Интеграл от безразмерной функции ИИС – вторая формула (7), получился I = 0,538. Максимальные (размерные) значения ИИС были рассчитаны по первой формуле (7). В таблицах

• 3,    4 представлены результаты расчета Jm ИИС по данным таблицы 1, в таблицах 5, 6 – по данным таблицы 2.

Таблица 3

Результаты расчета максимальных значений ИИС при изменении теплового потока (PV = 4 кПа, T = 40 °C, d = 10 мм) Results of calculation of maximum values of IIS with change of heat flow (PV = 4 kPa, T = 40 °C, d = 10 mm)

Номер по табл. 1	q	q	mk	Δ m	Jm
	кВт/м2	–	%	%	%/мин
1	2	0,333	86,0	14,0	0,0963
2	4	0,667	86,1	13,9	0,1077
3	6	1,0	86,2	13,8	0,1142
4	8	1,333	86,3	13,7	0,1216
5	10	1,667	86,4	13,6	0,1294

Таблица 4

Результаты расчета максимальных значений ИИС при изменении толщины слоя

( P = 4 кПа, T = 40 °C, q = 4 кВт/м²)

The results of calculating the maximum values of the AIS when changing the thickness of the layer (P = 4 kPa, T = 40 °C, q = 4 kW/m2)

Номер по табл. 1	d	δ	mk	Δ m	Jm
	мм	–	%	%	%/мин
6	5	0.5	85,8	14,2	0,1461
7	10	1,0	86,1	13,9	0,1077
8	15	1,5	86,3	13,7	0,0923
9	20	2,0	86,7	13,3	0,0821

Таблица 5

Результаты расчета максимальных значений ИИС при изменении остаточного давления ( T = 40 °C, d = 10 мм, q = 6 кВт/м²)

Results of calculation of maximum values of IIS with change of residual pressure ( T = 40 °C, d = 10 mm, q = 6 kW/m²)

Номер по табл. 2	P	p	mk	Δ m	Jm
	кПа	–	%	%	%/мин.
10	2	0,25	86,3	13,7	0,1103
11	3	0,5	86,3	13,7	0,1036
12	4	1,0	86,3	13,7	0,0988
13	5	1,25	86,3	13,7	0,0982
14	6	1,75	86,3	13,7	0,0972

Таблица 6

Результаты расчета максимальных значений ИИС при изменении температуры

( P = 4 кПа, d = 10 мм, q = 6 кВт/м²)

Results of calculation of maximum values of IIS with temperature change

( P = 4 kPa, d = 10 mm, q = 6 kW/m²)

Номер по табл. 2	T	p	mk	Δ m	Jm
	°C	–	%	%	%/мин
15	30	0,75	86,3	13,7	0,0860
16	40	1,0	86,3	13,7	0,1007
17	50	1,25	86,3	13,7	0,1322
18	60	1,5	86,3	13,7	0,1627

Расчетные значения Jm на рисунках 3, 4 показаны точками. Видно, что Jm увеличивается с ростом безразмерных величин теплового потока и температуры, уменьшается – с ростом отно- сительной толщины слоя и остаточного давле ния. Зависимость Jm от q и p можно аппрокси мировать линейной функцией (рис. 3, a; 4, a):

Jm ≡ ψ1( q ) = a 10 + a 11 q ; Jm ≡ f 1( p ) = c 10 + c 11 p .

Для аппроксимации зависимости Jm от δ и θ потребовался кубический многочлен

Jm ≡ ψ3( q ) = a 30 + a 31 q + a 32 q ² + a 33 q ³; Jm ≡ f 3(θ) = c 30 + c 31 θ + c 32 θ² + c 33 θ³.         (11)

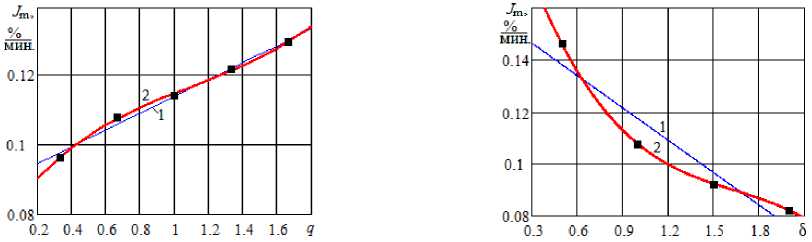
Рис. 3. Максимальные значения интенсивности испарения меда во время вакуумной сушки: a – при изменении относительного теплового потока, б – при изменении относительной толщины слоя (точки – по результатам экспериментов [6]; линии – расчет:

1 – линейная аппроксимация, 2 – кубическая по формуле (11)

Maximum values of honey evaporation intensity during vacuum drying: a – with a change in the relative heat flow, б – with a change in the relative layer thickness (dots – according to the results of experiments [6]; lines – calculation: 1 – linear approximation, 2 – cubic according to the formula (11)

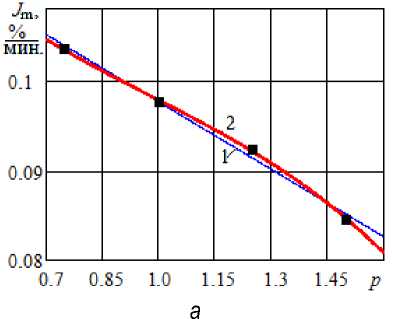
Рис. 4. Максимальные значения интенсивности испарения меда во время вакуумной сушки: a – при изменении относительного давления, б – при изменении относительной температуры (точки – по результатам экспериментов [7]; линии – расчет: 1 – линейная аппроксимация, 2 – кубическая по формуле (11)

Maximum values of honey evaporation intensity during vacuum drying: a – with a change in relative pressure, б – with a change in relative temperature (dots – according to the results of experiments [7]; lines – calculation: 1 – linear approximation, 2 – cubic according to the formula (11)

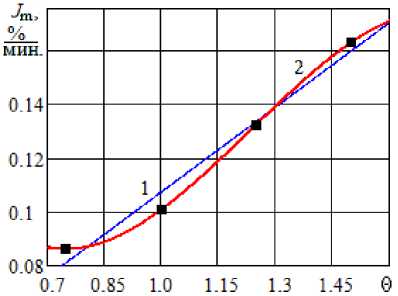
б

Рассчитанные Jm позволили исследовать с помощью математической модели динамику ИИС по формуле (5) и относительной массы объекта сушки по формуле (8) при различных значениях определяющих параметров. Результаты представлены на рисунках 5–10.

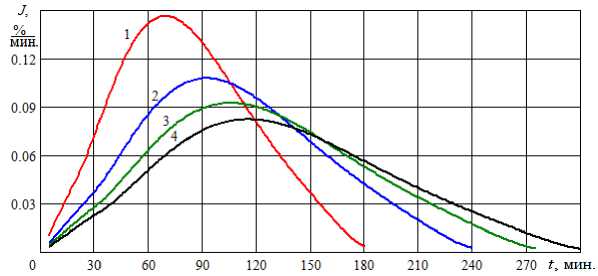
Рис. 5. Динамика изменения интенсивности испарения при вакуумной сушке меда с разной толщиной слоя: 1 – d = 5 мм, 2 – d = 10 мм, 3 – d = 15 мм, 4 – d = 20 мм Dynamics of changes in evaporation intensity during vacuum drying of honey with different layer thicknesses: 1 – d = 5 mm, 2 – d = 10 mm, 3 – d = 15 mm, 4 – d = 20 mm

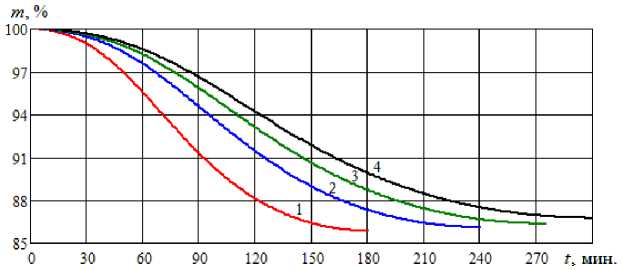
Рис. 6. Динамика изменения относительной массы меда при вакуумной сушке с разной толщиной слоя (обозначения, как на рис. 5) Dynamics of changes in the relative mass of honey during vacuum drying

with different layer thicknesses (designations as in Fig. 5)

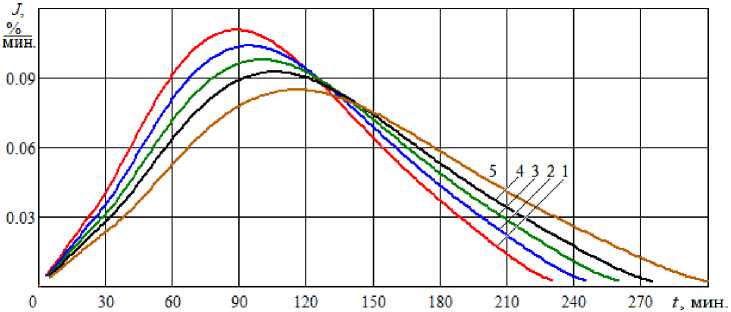
Рис. 7. Динамика изменения интенсивности испарения при вакуумной сушке меда с разным давлением: 1 – P = 2 кПа, 2 – P = 4 кПа, 3 – P = 6 кПа, 4 – P = 8 кПа, 5 – P = 10 кПа Dynamics of changes in evaporation intensity during vacuum drying of honey with different pressure: 1 – P = 2 kPa, 2 – P = 4 kPa, 3 – P = 6 kPa, 4 – P = 8 kPa, 5 – P = 10 kPa

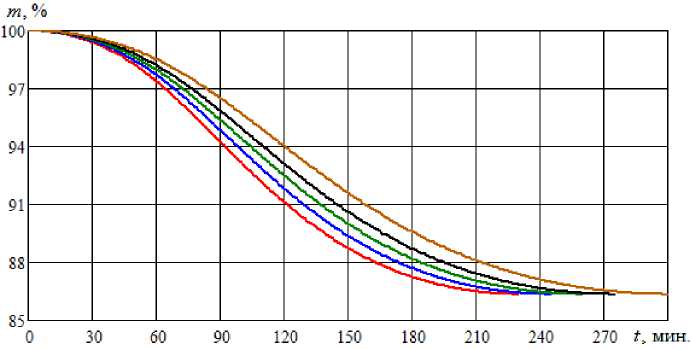
Рис. 8. Динамика изменения относительной массы меда при вакуумной сушке с разным давлением (обозначения, как на рис. 7)

Dynamics of changes in the relative mass of honey during vacuum drying with honey at different pressures (designations as in Fig. 7)

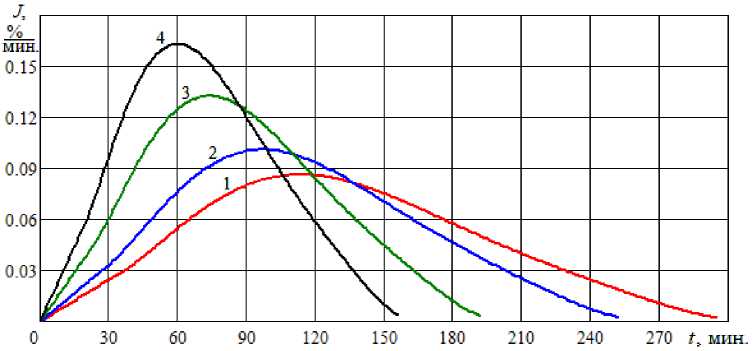
Рис. 9. Динамика изменения интенсивности испарения при вакуумной сушке меда с разной температурой: 1 – T = 30 °С, 2 – T = 40 °С, 3 – T = 50 °С, 4 – T = 60 °С Dynamics of changes in evaporation intensity during vacuum drying of honey at different temperatures: 1 – T = 30 °С, 2 – T = 40 °С, 3 – T = 50 °С, 4 – T = 60 °С

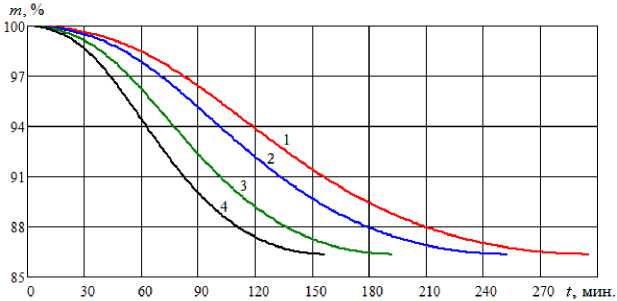
Рис. 10. Динамика изменения относительной массы меда при вакуумной сушке с меда с разной температурой (обозначения, как на рис. 9)

Dynamics of changes in the relative mass of honey during vacuum drying with honey at different temperatures (designations as in Fig. 9)

Графики изменения интенсивности испарения при вакуумной сушке меда (см. рис. 5, 7, 9) имеют ярко выраженные максимумы, соответствующие оптимальному времени сушки. Масса меда стабильно уменьшается с разной скоростью, имеются три ярко выраженных участка (см. рис. 6, 8, 10).

Чтобы использовать предложенную математическую модель для оценки влияния ИИС на газодинамические процессы в ВКС, как в [9], необходимо получить ИИС Θ в м3/мин по следующей формуле:

Θ = 0,01· J · M 0/ρn, (12)

где M 0 – исходная масса объекта сушки, кг; ρn – плотность насыщенных паров воды при температуре поверхности меда, кг/м³.

Заключение. Таким образом, цель исследования достигнута: исследовано влияние условий в вакуумной сушильной камере на интенсивность испарения при вакуумной сушке меда. Поставленные задачи выполнены: получена зависимость интенсивности испарения при суш-

ке меда от времени; рассчитаны максимальные значения интенсивности испарения при изменении теплового потока, толщины слоя, остаточного давления. Максимальные значения интенсивности испарения меда во время вакуумной сушки увеличиваются с ростом безразмерных величин теплового потока и температуры, уменьшаются – с ростом относительной толщины слоя и остаточного давления. Графики изменения интенсивности испарения при вакуумной сушке меда по времени имеют ярко выраженные максимумы, соответствующие оптимальному времени сушки. При толщине слоя d = 5 мм – 70 мин, d = 20 мм – 120 мин; при давлении P = 2 кПа – 90 мин, P = 10 кПа – 120 мин; при температуре: T = 30 °С – 120 мин, при температуре T = 60 °С – 60 мин. Предложенная математическая модель позволяет рассчитать динамику изменения интенсивности испарения во время вакуумной сушки меда при различных значениях определяющих параметров. Что позволит применить метод исследования газодинамических процессов ВКС, разработанный в [9].