Моделирование технологической линии для производства желейно-фруктового мармелада из мякоти плодов черёмухи

Введение. Мармелад из мякоти плодов черёмухи занимает особое место в функциональном питании. Его основой являются натуральные и полезные вещества (фруктоза, глюкоза, сахароза, пектин, органические кислоты, аминокислоты, Р-активные вещества, витамины А, Е, С, микроэлементы – магний, калий, медь, железо, кальций), которые не содержат калорий, улучшают функционирование организма, выводят токсины, снижают уровень холестерина [1].

Существующие технологические схемы производства мармеладов используют различные виды ягод (малина, крыжовник, смородина, вишня и т.д.) и фруктов (айва, яблоки, абрикосы и др.) [2, 5]. Черёмуху в этом виде кондитерского изделия не используют. В работе предлагается модернизировать линию по производству мармелада и заменить сырьё на мякоть плодов черёмухи. Это связано с широким ареалом произрастания и низкой себестоимостью сырья [3].

Согласование рецептуры по основным ингредиентам мармелада с режимными параметрами его производства направлено на создание нового функционального продукта с высокими органолептическими качествами.

Важнейшей задачей по модернизации кондитерского производства мармелада является автоматизация основных технологических звеньев и процессов с доведением до предельного состояния выпуска продукции. В связи со сказанным необходимо уделить особое внимание упаковке и расфасовке продукции, выпуску в удобном для потребителя виде.

Актуальность исследований. Замена трудоёмких процессов на разрабатываемые переналаживающиеся поточные линии позволит создать новый продукт потребления с функциональными свойствами. Мо- делирование и оптимизация технологической линии позволят выбрать эффективные режимные параметры для получения желейно-фруктового мармелада из мякоти плодов черёмухи. Предложенная линия обеспечит изготовление мармелада с содержанием функционального сырья (мякоти плодов черёмухи) с минимальным числом оборудования.

Цель исследований. Разработка проекта и модели формирования непрерывной линии для массового производства желейно-фруктового мармелада из мякоти плодов черёмухи, исследование технических процессов и финального состояния аппаратно-машинной системы.

Объекты и методы исследований. Закономерности изменения нагрузки на звенья технологической линии, переходные процессы, режимы производства желейно-фруктового мармелада из мякоти плодов черёмухи. Использован аппарат математического моделирования пакета Maple.

Результаты исследований и их обсуждения. Предлагаемый проект технологической линии включает в себя принципиальную схему с циклом обработки сырья и с учётом размещения машин для тепловой, механической обработки, получения изделий отливкой и их упаковки (рис.).

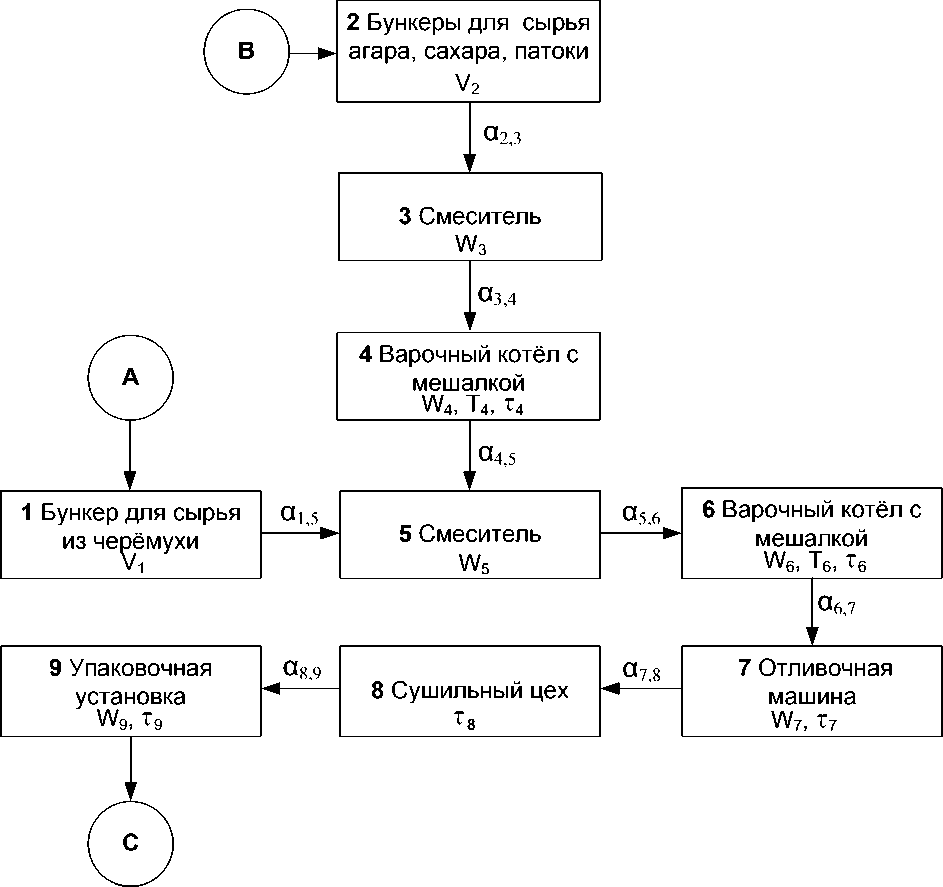
Аппаратно-машинная схема поточного производства желейно-фруктового мармелада из мякоти плодов черёмухи

Для того чтобы применить математический аппарат для изучения функционирования аппаратномашинной схемы, разработаем математическую модель этой системы. Прежде всего определяем совокуп- ность технических средств и режимных параметров, которые будут служить количественными характеристиками. Затем установим соотношения между состоянием звеньев, интенсивностями, системы в целом (табл.).

Состав аппаратно-машинной схемы

Звено	Название, модель оборудования	Модельные параметры
1	Бункер	7 1
2	Бункер	^ 2
3	Смеситель-гомоненизатор ГМ-ГУРТ; МГ-УГМ; ССК-Пб100лАСУ; ССК-БК-170лАСУ	72,W2 ,^ 3
4	Котёл КПЭ 60; КПЭ 100	7 2 , T4, Т 4 , Ш 3 , Ш 4
5	Смеситель-гомоненизатор ГМ-ГУРТ; МГ-УГМ; ССК-Пб250лАСУ; ССК-БК-170лАСУ	7 1 , 7 2 , T 4 , Т 4 , Ш 4 , Ш 5
6	Котёл КПЭ 160; КПЭ 250	7 1 ,7 2 , Т б , Т б ,Ш 5 ,Ш б
7	Отливочная машина АК-1023 MOULDTRAY-200; АК-1021 MULTICAST-200	7 1 ,7 2 , T6, т6, т7 ,Ш6,Ш7
8	Сушильный цех (сушильные шкафы МХШС-01; МХШС-01-К; Универсал-СД-3)	71 , 72 , Т8
9	Упаковочная установка ВН-500; МГУ-НОТИС-135	7 1 ,7 2 , Т 8 , Т9,Ш9

Эксплуатация технологической линии предусматривает три этапа: начальный (1–5), основной (5–6), завершающий (7–9).

Мякоть плодов черёмухи в качестве исходного сырья поступает в бункер 1 , и параллельно агар, сахар и патока – в бункер 2 . Затем сырьё из бункера 2 поступает в смеситель 3 , и далее в течение 5 минут происходит приготовление агаро-сахаро-паточного сиропа в варочном котле с мешалкой 4 , где сироп уваривают до массовой доли сухих веществ 73–77 %. Этот сироп является полуфабрикатом мармелада. Мякоть плодов черёмухи из бункера 1 и сироп из варочного котла 4 одновременно поступают в смеситель 5 , из которого попадают в варочный котёл с мешалкой 6 для приготовления мармеладной массы. Смешивание сырья лимитируется временными нормами 5–7 минут. Процесс варки происходит при температуре 106–108 °С. После варки мармеладная масса поступает в отливочную машину 7 , с помощью которой происходит заполнение форм для формирования и студнеобразования мармеладной массы. Студнеобразование происходит в течение 40 минут при температуре 70 °С.

Сушка и охлаждение мармелада производятся в сушильном цехе 8 при температуре 45 °С в течение 15 часов, а после мармелад охлаждается при температуре 10–15 °С в течение 2 часов. Далее следует упаковка и маркирование в упаковочной установке 9 .

Для разработки аналитической модели введём следующие обозначения для звеньев и интенсивностей потоков между ними: X k - k-е звено технологической линии, a *, k+i : X k ^ X k+i - интенсивность потока из k-го звена в (k+1)-е. Обозначим функцию состояния звена X k в момент времени t через x k (t). Изменение состояния звена описывается разностью входящих и исходящих потоков по временному параметру t. Например, состояние звена 3 характеризуется дифференциальным уравнением первого порядка

* 3 (7 2 , Ш₂, Ш 3 , t) = « 2,3 (7 2 ) • * 2 (7 2 , t) - a_; Л'Л) • * 3 (7 2 , W₂, Ш 3 ,0

и начальным условием х з (0) = 0, в котором интенсивность «₂ , ₃ зависит от объёма бункера V 2 , «₃ , ₄ - от скорости смешивания W 3 , соответственно процессы в звеньях 2 и 3 имеют режимные параметры 7₂,Ш₃,Ш₄ . На начало процесса при t=0 полагаем, что в смесителе не содержится сырьё.

Модель функционирования линии представим системой дифференциальных уравнений с учётом режимных параметров:

• * 1 (7 1 , t) = «^%_л ⁽ t) - « 1,5 * 101 , t) ,                            (1)

• * 2O2 , t) = « в • *_B ⁽ t) - « 2,3 02 ) • X 2O2 , t) ,

Х з (Ц И 2 , И з , t) = а₂₃(У₂) • x₂(Ц t) - « з_Д (И з ) • Х з (Ц И 2 , И з , t) ,

Х 4 (^ 2 , Т 4 , Т 4 , И з , И 4 , t) = « з,4 (И з ) • Х з01 ^ 2 , И з , t) —

-« 4,5 (^ 5 ) -X 4 (У* T 4 , Т 4 , И зЖ, t) ,

Х 5 01 ^ 2 , T4, Т 4 , И 4 , И 5 , t) = « 1,5 (У 1 ) • Х 1 (Ц t) +

+ « 4,5 (И 5 ) • Х 4 (У₂, 7 4 T 4 , И з , И 4 , t) - « 5,6 (И 5 ) • Х₅(Ц У₂, T 4 , Т 4 , И 4 , И 5 , t) ,

Х б (У 1 , У₂, Т б , Т б ,И 5 ,И б , t) = « 5,б (И 5 ) • Х 5 (У 1 , У₂, T 4 ,1 4 ,И 4 ,И 5 , t) -

-« 6,7 (Т б , Т б , И б ) • Х б (Ц Ч Т б , Т б , И 5 , И б , t) ,

Х 701 У 2 ,Т б ,Т б ,Т 7 , И б , И 7 , t) = « б,7 (Т б ,Т б , И б ) • Х б (ЦУ 2 ,Т б ,Т б , И 5 , И б , t) --« 7, ₈(И 7 , Т 7 ) • Х₇(Ц У, Т б , Т б , Т 7 , И б , И 7 , t) ,

^Х8 ^(У1 , ^У2 , ^Т8 , ^t) = « 7,8^(И7 , ^Т7 ) ’ ^Х?01 ^У2 , ^Тб , ^Тб , ^Т7 , ^Иб , ^И7 , ^{t) -}

-« 8,9 (Т 8 ) -Х 801 У г , Т 8 , t) ,

Х 901 ^ 2 , Т 8 , Т 9 , И 9 , t) = « 8,9⁽ Т 8 ) • Х 8⁽ У 1 , 11 Т 8 , t) -

-« С -Х 9 (У 1 , У₂, Т 8 , Т 9 ,И 9 , t) .

За начало процесса примем t=0, соответствующее загрузке сырья в бункеры 1 и 2, и поставим начальные условия для системы уравнений (1). В звеньях 1 и 2 имеется изначальный объём сырья a и b, а звенья 3-9 имеют нулевое значение, так как в момент времени t=0 в них не происходит никаких процессов. Таким образом получим x1(0) = a, x2(0) = b,                                                    (2)

x3(0) = 0, x4(0) = 0, x5(0) = 0, x6(0) = 0, x7(0) = 0, x8(0) = 0, x9(0) = 0, где a – объём сырья в бункере 1; b – в бункере 2.

Поставленная задача Коши (1)–(2) является математической моделью системы переходных процессов, а её решение описывает динамику отдельных технологических процессов и состояний звеньев.

Исследуем финитное состояние технологической системы, составив и решив систему линейных уравнений, соответствующих исходной системе (1):

« л • Х_Л1) - « 1.5 Х 101 1) = 0 ,                             (3)

« В • X_в ⁽ t ⁾ - « 2,з⁽ У 2 ) • Х 2⁽ ^ 2 , t) = 0 ,

« 23О2 ) • ^Х2^(У2 , ^{t) -} « з,4^(Из ) • ^Хз^(У2 , ^И2 , ^Из , ^t) = 0 ,

« з,4 (И з ) • Х з (Ч И 2 , И з , t) - « 4,5 (И 5 ) • Х₄(Ц Т 4 , Т 4 , И з , И 4 , t) = 0 ,

« 1,5^1 ) -Х 101 t)-« 5,б (И 5 ) -Х₅0 1 У 2 , Т 4 , Т 4 ,И 4 ,И 5 , t) =0,

« 5,б (И 5 ) • Х 5 (Ц Ч Т 4 , Т 4 , И₄, И 5 , t)

-« б,7 (Т б , Т б , И б ) • Х б (Ц Ч Т б , Т б , И 5 , И б , t) = 0

« б,7 (Т б ,Т б , И б ) • Х б (ЦЧТ б ,Т б , И 5 , И б , t) -

-« 7,8 (И 7 , Т 7 ) -Х₇01 У, Т б , Т б , Т 7 ,И б ,И 7 , t) = 0

« 7,8 (И 7 , Т 7 ) • Х₇(У 1 , Ч Т б , Т б , Т 7 , И б , И 7 , t) -

-а₈ ,9 (> 8 ) - Х е 01 , ^ 2 , * 8 , 0 = 0 ,

« 8,9 (Т₈) • Х 8 (V i , У 2 , Т₈, t) — «_с • X 9 (V i , У 2 , Т₈, T 9 , W 9 , t) = 0 .

В результате решения данной системы с помощью Maple получены соотношения, связывающие интенсивность с состоянием звеньев:

а_А • х_а (t)

^'^ т^             (4)

а • xB (t) X2W2,')= * л , а2,3(^2) _              ' ав • хв (t) X3(VM, ') = a3,t(W3y ,                     ' ав^хв (t) • Х4(^2, Т4, T4, W3, W4, t) = *         , а4,5 (W5) аА • ха (t) • ав • xB (t) x5(Ki, V2, Т4, *4, W4, w5, t) = а ^а5 (W*) *, ал-хл (t) • ав • xB (t) Х6(V1,V2,Тб,т6, W5,W6,t) = А А ;   *   *V }, а67(Т6, T6, W6) аА • ха (t) • ав • хв (') Х7 (Vi, V2, Т6, T6, т7, W6, W7, t) = А А       В В , а7,8(W7, T7) г               «а •ха(') • а* • Х* (') Х8 (V1, V2, T8, ') =                          , а8,9 (T8) ш Л аА^ХА(О • а* • Х* (') Х9(V1, V2, T8, T9, W9, ') =                          , ас зависящие от соотношения объёмов бункеров 1 и 2. Соотношение объёмов регулируется заданной рецептурой, поэтому с учётом системы [4] технологическую линию всегда можно адаптировать под конечный продукт.

Перспектива развития модельного подхода лежит в плоскости обобщения сырья с учётом его реологических свойств, и, соответственно, предложенный подход делает возможной модернизацию технологической линии для других плодово-ягодных смесей.

Выводы

• 1.    Разработанные принципиальная схема и математическая модель аппаратно-машинной системы производства нового функционального продукта – желейно-фруктового мармелада из мякоти плодов черёмухи – позволяют подобирать режимные параметры и соотношение компонентов сырья под конкретную рецептуру.

• 2.    Вычисленные закономерности изменения нагрузки на звенья технологической линии, технология и средства предложенной аппаратно-машинной схемы могут быть использованы в производственных предприятиях АПК.