Нестационарная космологическая модель с метрикой типа Геделя в теории Эйнштейна-Картана

При обсуждении моделей с вращением представляется разумным учитывать наличие спина (внутреннего углового момента) космологической материи. Ее элементами в современную эпоху можно считать галактики (или кластеры галактик), а в ранние космологические эпохи – элементарные частицы. Описание такой материи и соответствующей динамики гравитационного поля дает калибровочная теория для групп Пуанкаре [1, 2].

Простейшей моделью такой теории является теория Эйнштейна–Картана (естественное обобщение ОТО). Эта теория принимает в расчет спиновые частицы материи и описывает их влияние на геометрическую структуру пространства-времени, которое характеризуется нетривиальными кривизной и кручением. Отметим, что впервые в работах Д.Д. Иваненко, В.А. Короткого, Ю.Н. Обухова [3, 4] в квадратичной пуанкаре-калибро-вочной теории гравитации с кручением построены нестационарные, несингулярные, всюду причинные космологические модели вращающейся Вселенной, заполненной спи-нирующей материей.

В работе [5] Ю.Н. Обуховым и В.А. Коротким при построении вариационной теории жидкости Вейсенхоффа в пространстве-времени Римана–Картана показано, что уравнения Эйнштейна–Картана могут быть сведены к эффективным уравнениям Эйнштейна:

R._f-g g^R^T 1ф ‘ ж ^В'     (1)

и к уравнению для кручения :

Q      S u .            (2)

В уравнении (1) все компоненты, связанные с кручением , перенесены в правую часть, в результате для нейтральной спиновой жидкости Вейсенхоффа

Tэфф (   )_ рэфф gafi+uaufi (рэфф+8эфф )^

- 2( g^^U )УД u (а S, )J, где рэфф= P-XS2, 8эфф=8-ks*.(4)

В [5] S – тензор плотности спина – подчиняется уравнению

S'- u'uS- u-uS'a,(5)

где Sa/3 = VA u^Sa^ , u^ - 4-скорость жид- кости, скалярная плотность спина

S;=g s^1-(6)

Представляет интерес в теории Эйн-штейна–Картана построение космологических моделей с вращением, заполненных не только жидкостью Вейсенхоффа, но также и другими источниками (в этом случае в правой части (1) к T фф ( ж ' В ') нужно прибавить ТЭИ этих источников). Например, в качестве такого до-

(В силу (12) в сопутствующей системе отсчета q ₀ = 0).

Уравнение теплопроводности запишем в следующем виде:

q_a=k(8^p_a u_Uy ) T тТа_р ,   (13)

где k – коэффициент теплопроводности; T –

полнительного источника можно взять анизотропную жидкость с ТЭИ:

^Т_ар = (P+u)^u_aUp +(р-я)Х_аХg-ng7₀, (7) где u^ = 1, X_VX^V = -1, и% =°, Р>^ Отт (анизотропная жидкость в космологии с вращением использовалась в [6–8] и других работах). Однако мы вместо двух жидкостей (спинирующей жидкости и анизотропной жидкости) введем одну – анизотропную жидкость Вейсенхоффа, постулируя следующий эффективный ТЭИ анизотропной жидкости Вейсенхоффа:

Taft        uua^f} ⁽ ^эфф+^эфф ) + ( ^эфф ЭФффф ⁾ХаХfl Э^эфд Safl (8)

- 2( f+uV )VJ u _{а s

температура; a ( a u u ).

–

ускорение жидкости

Для наших источников эффективные уравнения Эйнштейна (по аналогии с (1)) будут иметь следующий вид:

R _ 1

'-      2

__vs T эфф ( а . ж . В .)     пи.. и .     т.т . п .

T   TT

,

где лэфф=^ S> . £ффф=£-KS2, (ддф=a-^S2, (9)

s,сг,я - соответственно плотность энергии и компоненты анизотропного давления анизотропной жидкости Вейсенхоффа,

£> 0, су > я.            (10)

S – тензор плотности спина, подчиняющийся уравнению (5); S – скалярная плотность спина (6);    – вектор анизотропии,

¹ Х^и^ =0.

Итак, в данной статье мы найдем нестационарное космологическое решение типа Геделя в теории Эйнштейна–Картана, когда источниками являются: анизотропная жидкость Вейсенхоффа (с эффективным ТЭИ (8)), чистое излучение и тепловой поток.

ТЭИ чистого излучения имеет вид T*и • = wkakp, причем k – вектор чистого излучения удов-

(14) а уравнения для кручения сохраняют вид (2). Нестационарное решение уравнений (14) будем искать для метрики типа Геделя вида ds2 = dt2-2^Remxdydt-R2dx2-R2dz2, (15) где R = R(t) >0, cp- (t)t).

Мы считаем, что у нас система отсчета сопутствующая, т.е. u . Тогда тензор вращения для нашей модели имеет вид

,p m (t) em 8^,

Д XP   lml co = A—eo^oco p =—.

V 2 ^ap      2 R

Тензор сдвига имеет следующие ненулевые компоненты:

°П “ °33 “ _Q ^R , 3 (p

\¹ СУ = J—cy '

X 2

Расширение

2 .      -

= ² e^{2 mx}R

²²    3

_ 1

3~ Уз

0=R 1

R Вектор ускорения

.2 •

,

ф_

(р

.

летворяет уравнению kk =0.            (11)

ТЭИ теплового потока т. п.

ар ~ qaup+qpua ,

a_a= -(RR + Rp ) e ^m 8²_a.

Считая, что спин жидкости направлен вдоль оси z, запишем тензор плотности спина в виде

Тогда

S^ =2 S ^.

S = S 12= s_S 21 .

Решение уравнения (1) дает

где q – вектор теплового потока, qaua =0.                (12)

₌ S 0 ( x )

R

Для расчета различных геометрических величин и записи эффективных уравнений Эйнштейна удобно использовать тетрадный формализм. Выберем ортонормированную тетраду в виде h = 1, h€ = emxR^R, h1 = h€ = R, h = e^R.

Остальные компоненты тетрады равны нулю. Локально - лоренцевы тетрадные индексы здесь отмечены "шляпкой" (в дальнейшем это обозначение в полевых уравнениях мы опустим). Большими буквами будем обозначать тетрадные индексы различных величин.

Аналогично [5] тензор плотности спина жидкости можно определить в виде

S„, =1 рАЩав, ,       (21)

где р_АВ - спиновая плотность в частице жидкости (р_Ав =2//^^); р - плотность частиц анизотропной жидкости Вейсенхоффа.

Плотность частиц жидкости   удовле творяет уравнению непрерывности [5]:

V_a ри^а =0.

Решение этого уравнения в нашем случае есть

/>=4-,(

R ³

где р_й = const .

На основании (21) и (22) получим

1 emx 0 1€2€

S Sn.

¹²   2 R 2 R

Если в (19) считать S / e— = const, то с учетом (23) получим р = const (что аналогично с [5] соответствует постоянству плотности спина в каждой частице жидкости).

Вычисление скалярной плотности спина

S_c дает

0Q0 C- 2 R 3И -R >|’ где

0 .

В сопутствующей системе 0АА отсчета

и_А = ^и ^{и =} ^о ; пусть вектор анизотропии жидкости направлен по оси х -ов: ^_А = —5\ .

С учетом этих замечаний эффективные уравнения Эйнштейна с космологическим членом (14) для метрики (15) в тетрадном ба зисе (20) запишутся следующим образом:

m2  2 mQ2

2 F             ⁰

4R2      R4        эфф0

31 3 B C 2    wk0k1

R

2                  m ²

F wk k q , 0 2    2    _{4 R} 2

mQ _{0               wk} 2 _,

_R 4                 эфф       1   ^,

R 3¹ 3 B C ²

эфф ^wk 2 ²

m2

wk k ,   2 F

^{1 2}              4 R ² R ⁴

m-К = Ф<4_эфф + wk 322

4R wk k q 0, wk k wk k 0.

Здесь введены следующие обозначения:

П                                             •

F = — , B = — р³ R ²3 C = Qo^, (27)

R 2

Qo = const определено выражением (25); диф- ференцирование в (27) производится по переменной t;

эфф          Sc2,   эфф          Sc2,   эфф

К системе (26) добавляется уравнение kAkA = k.2 - k2 - k,2 - k2 = 0.

A 0123

Рассмотрим случай, когда kk0, а также qi = Pq3, Р = const > 0.

Тогда из (26) получим

B+Cp ² =0.

Решением этого уравнения с учетом (27) будет

R —------.(30^

m

Далее из (28) следует, что k₀ = ±k ₃.

Пусть k₀ = —k₃ = k .

Тогда из системы (26) и (29) имеем wk2=—U B-Cp2.    (31)

pR ³³

Из (31) и (26) с учетом (30) можно получить уравнение для ср :

a

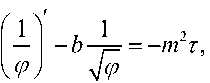
где

2 Q    22 Q0m a =----0, b = —-------, T = t + q, mp q = const > 0, QQm > 0, дифференцирование в (32) по т . Уравнение (32) имеет решение

8 Q 0 p ²

_h 2 _m 3 2 ^,

где h = 1 + J1-2 p2 = const,  0 < p<    .  (34)

Тогда из (30) найдем: h\m\r

R

2 p

.

Для данных R и ср вычислим материальные параметры модели: S_c ((из (24)), 8, л, ст (из (26)), wk 02 = wk 32 (из (31)), q i , q 2 , q₃ (из (26) и (29)). В результате будем иметь

S              ,

h

22 4 wk_n = wk. =---- 7-,

03 _h 2 ^£ = Л- -8-, h ²

Х7Г = -Л h ²

4p*sign(m) qi   pq3           7 2     , h2

2 q 2 ~       2".

Неравенства (10) будут выполняться, если

А-±>0.

hq ²

(Заметим: отсюда следует, что Л>0). Уравнение для кручения (2) в тетрадной форме можно переписать в виде [5]

QA=^uASB с. BCBC

На основании (23), (25) ненулевые тетрадные компоненты кручения для нашей модели будут

Q0€Q0€S     h1h2S       SQ

1€2€          2€1€ 1€2€ 1€  2€  12 R2emx

.

В итоге ненулевые тетрадные компоненты тензора кручения:

о € = -0^s = Р * sign ^{( m})

1€2€             2€1€

Уравнение теплопроводности (13) для решения (33) и (35) дает

2m2m kT = —, к T- =-4, kT= ^.

,_,              3, _p

Решение этой системы дает для температуры xz

T^G e^p 0.

та

Коэффициент теплопроводности xz k H   1e   p

В (36) и (37) G , H,Р,а - постоянные, G > 0,

2 m

H           0,     (    1) m 0,     0.

G

Здесь мы также феноменологически предполагаем, что тепло выделяется в нашей модели в ходе некоторых экзотермических процессов.

Рассмотрим динамические параметры нашей космологической модели. Из (16), (17) и (18) найдем вращение, сдвиг и расширение:

p со = —, h

^, 3

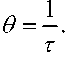
Отсюда видно, что с ростом времени (т = t + q) вращение, сдвиг и расширение за тухают (тоже затухает и "квадрат 4-ускорения" а2 ). Из (38), (34) следует, что за счет подбора константы p можно согласовать скорость вращения нашей космологической модели со скоростью вращения Вселенной, полученной из наблюдений. Эволюция нашей модели начинается с момента времени t = 0 и при этом найденное космологическое решение будет несингулярным (при t >0).

Отметим, что оно будет и причинным. Это легко показать, если применить рассуждения, изложенные в конце предыдущего параграфа, к метрике (15).

Отметим здесь, что А.М. Галиахметов в [9] также получил в рамках теории Эйнштей-на–Картана точное частное решение для вращающихся вселенных, заполненных анизотропной жидкостью и неминимально связанным скалярным полем.