О захваченных волнах в акустическом волноводе с бесконечно тонким препятствием

Во многих областях физики имеет важное значение исследование собственных колебаний в неограниченных волноводных областях. Первые известные исследования спектральных свойств лапласиана в областях с бесконечной границей были проведены Реллихом [1] в 1940-е гг. и чуть позднее – Джоунсом [2]. В частности, ими было показано, что лапласиан имеет собственные значения для класса локальных возмущений достаточно гладких полуцилиндрических областей. Возрождение интереса к данной тематике в последнее время обусловлено в первую очередь актуальностью исследования аэроакустического резонанса, например, в турбомашинах (газовых, паровых и гидравлических турбинах, насосах, компрессорах), трубопроводах и т.п. (обзор некоторых работ экспериментального характера содержится в работе [3]). Отметим работы [7,11], в которых рассмотрены случаи цилиндрических тонкостенных препятствий в волноводе, и работу [8], где проведено численное исследование акустического резонанса около крестообразного препятствия, образованного двумя прямоугольными пластинами в канале квадратного сечения. Необходимо также упомянуть работы [13-16], в которых рассматривается метод изучения собственных колебаний, основанный на свойствах расширенной матрицы рассеяния.

В работе рассматривается математическая модель акустических резонансных явлений около бесконечно тонких перегородок в волноводе прямоугольного сечения. Препятствия такого вида широко используются в аэродинамике для выпрямления потока газа [8].

Рассматривается область:

Q 0 = {( x , y , z ) e R³ : x e ( - d 1 , d 1 ), у e ( - d 2 , d 2 ), z e R },           (1)

которая моделирует волновод. В нем помещено препятствие B , симметричное относительно координатных плоскостей x = 0 и у = 0. Множество B представляет собой объединение двух бесконечно тонких пластин B 1 и B ₂ ненулевой площади, расположенных в плоскостях x = 0 и у = 0 соответственно, симметрично относительно оси O z . Пластины B 1 и B ₂, границы которых достаточно гладкие, пересекаются, образуя крестообразное препятствие. Предполагается, что

B 1 n B ₂ = {( x , у , z ) e Q ₀: x = 0, у = 0, a <  z <  b} и существует 5 >  0 такое, что множество

B j n {( x , у , z ) eQ ₀: x ² + у ² <  5 , a <  z <  b } является прямоугольником ( j = 1, 2).

Рассматривается краевая задача Неймана для уравнения Гельмгольца

.         .                             Гн

( А + Л ) и = 0 в Q = Q₀ \ B , — = 0 на dQ ,              (2)

0      дЯ описывающая колебания акустических волн. Здесь Л = to2 / c2, to - частота акустических колебаний, с - скорость звука, Я - вектор внешней нормали к dQ. Известно, что дискретный спектр задачи (2) пуст, т.е. собственные значения (если они существуют) могут быть вложены в непрерывный спектр задачи, который заполняет неотрицательную полуось [0,+ »).

Далее будут использованы обозначения:

K^a = {( x , у , z ) e R ³ : x >  0, у >  0}, Q ^a = Qn K^a , B^a = B n K^a , dQ ^a =SQn K^a , Г = X и Y , Г ^a =Г n K^a , где X (соответственно Y ) есть проекция множества Q на плоскость у = 0 ( x = 0 - соответственно).

Цель работы - показать существование собственных значений, принадлежащих интервалу (0, Л ² ₀), где Л ² ₀ = п ²/ (4 d 1² ) + п ²/ (4 d ₂ ² ). Для этого применяется прием постановки искусственных краевых условий Дирихле [10] на плоскостях симметрии. Рассмотрим сужение задачи (2) на четверть волновода Q ^a

a

( А + Л ) u a = 0 в Q a , ---- = 0 на dQ a , u a = 0 на Г a .          (3)

д Я

Непрерывный спектр же задачи (3) в отличие от спектра задачи (2) заполняет промежуток [Л20, + ”), а левее точки отсечки Л20 могут существовать собственные значения задачи (3). Очевидно, что если Л есть собственное значение задачи (3), то оно является собственным значением задачи (2). В самом деле, если ua есть собственная функция задачи (3), соответствующая Л, то можно определить функцию ua(x,y,z) для (x,y,z) G Qa, u (x, y, z) = <

- u a ( - x , y , z )

- u ^a ( x , - y , z )

_ u a ( - x , - y , z )

для ( x , y , z ) gQ , x <  0, y >  0, для ( x , y , z ) gQ , x >  0, y <  0, для ( x , y , z ) gQ , x <  0, y <  0,

которая будет являться собственной функцией задачи (2) из H ¹ ( Q ), соответствующей тому же самому собственному значению Л * . Отметим, что наличие нетривиальных решений задачи (2), исчезающих на бесконечности (захваченных волн), может привести к явлению резонанса, т.е. к аккумуляции энергии в ограниченных областях.

Через C” обозначим подмножество класса бесконечно дифференци руемых функций в Qa, обладающих свойствами а) u (x, y, z) = 0 для (x, y, z) g Гa,

б) носитель u(x, y, z) ограничен в Qa . На C” определим полунорму г                                          2

II u | 1= Ш uud Q + Ш ( ^ u"^u ) d Q

a

a

где dО = dxdydz. Обозначим через H0 пространство Соболева, полученное замыканием C0” в полунорме (4).

Доказательство существования собственных значений левее точки отсечки Л20 проводится вариационным методом [10-12, 15, 16]). Имеет ме- сто

Лемма 1 [4]. Пусть

Л _о

ш^ ^| d Q

= inf ^ a ----2-----

^H ⁰ Ш k l ^{d Q}

Q a

.

Тогда Л ₀ < Л ² ₀ .

Более того , если

Л0 <Л2, то Л0 - наименьшее собственное значение задачи (3), и если

Л о =Л ²о ,

то в интервале ( -да , Л ² ₀) не существует собственных значений задачи (3) .

Известно, что для ограниченных областей выражение (5) дает величину наименьшего собственного значения соответствующего самосопряженного расширения оператора Лапласа ( - А), но в случае неограниченных областей Л ₀ может быть как собственным значением, так и нижней границей непрерывного спектра.

Введем некоторые обозначения. Пусть р(т) - достаточно гладкая чет ная функция, такая, что р(т) = 1,     если т < 1, '

р ( т ) = 0,    если Т ^ 2,

0 <  р ( т ) <  1, если 1 < | Т <  2.

Пусть г > 0, D £ - множество на плоскости Oyz

D \ = { (0, У , z ) e B 1 : dist ((0, y , z ), S B J <  £ } .

Пусть x_£ ( x , z ) - достаточно гладкая функция, такая, что Х г ⁽ У , z ) = ¹     если ^(0, У , z ) ^e B 1 \ ^D £ ,

Х г ( У , z ) = 0,     если (0, y , z ) eQ ,

0 <  Х г ( У , z ) <  1, если (0, У , z ) e D £

Аналогично определяются множество D в плоскости Oxz и доста точно гладкая функция пг(x, z):

D £ = { ( x ,0, z ) e B ₂: dist (( x ,0, z ), d B ₂) <  £ } ,

П ( x , z ) = 1,      если ( x ,0, z ) e B 2 \ D ²,

П г ( x , z ) = 0,     если ( x ,0, z ) eQ ,

0 <  n ( x , z ) <  1, если ( x ,0, z ) e D ².

Имеет место

Теорема 1. Пусть множество B - объединение двух бесконечно тонких пластин Bi и B2 ненулевой площади, расположенных в плоскостях x = 0 и у = 0 соответственно, симметрично относительно оси Oz. Предполагается , что пластины имеют достаточно гладкую границу, B1 n B2 = {(x, у, z) e Q0: x = 0, y = 0, a < z < b} и существует 5 > 0 такое, что множество Bj n {(x, y, z) e Q0: x2 + y2 < 5, a < z < b} является прямо угольником (j' = 1, 2). Тогда задача (2) имеет собственное значение, которое принадлежит интервалу (0, Л20).

Доказательство . Рассмотрим пробную функцию

У = Sin

n x I .

sn

V ui)

f п у If z I 1

¹ p |^J ^{+ (} P ^{( R} у ) ^{n ( x} , ^z ) ⁺ P ^{( R x} ) Х г ⁽ У , ^z )), v 2 d 2 ) V R ) R

(11) где а , в , R >  0. Очевидно, что функция у ( x , у , z ) для достаточно большого R принадлежит H ₀ ¹ .

Для доказательства теоремы достаточно доказать неравенство

' Ш I k^{2 d} Q H ' У^{2 d} q 0

Q a

Q a

для достаточно большого R и достаточно малого фиксированного £ > 0. В самом деле, из неравенства (12), согласно лемме 1, следует существование наименьшего собственного значения задачи (3) в интервале (0, Л ² ₀), которое является собственным значением и для задачи (2). Из вида функции у ( x , у , z ) получаем

У |² = sin ²

г n x 1-2 sin2

Id

V^ui )

—^ | p ² 1 — | + -^p p ² ( R ^a у ) n_E 2 ( x , z ) + 2 d ₂ ) V R ) R ^{2 e           £}

+ -L P ² ( R ^a x ) x £ ( У , z ) +

R

+—sin R ^e

n x I .

sin

2/7 V ^ui)

— ^ | p | z I P ( R ^a у ) n ( x , z ) + ~s sin 2 d ₂ J V R )                  R ^e

n x I . sin

2/7

V ui )

2 d ₂

( Z lz„x          2

^x p |^l P ^{( R x} ) X ⁽ у , z )⁺ ^ e P ^{( R} у ) П ^{( x} , z ) P ^{( R x} ) X_E ⁽ У , z ), V R )                 R

I V k ² = ^ y cos ² 4 d 1²

^f n x ¹ .

2^ J ™

Vui )

2 f п у I у f z I+— V 2 d 2 ) ^p V R ) R ’ '

P 2 ( R a У )^

+ -ipU ( p R^ax ) ) 2 x ;( У . z ) +

R

n cos

R ^e d 1

V

5 x

I +

■ пу I f z I Sin —— I p | — |x

V 2 d 2 ) V R )

p ( R ^a y ) ^дПг- + — ^ — cos

^V      d x   R ^e-a d 1

sin ^ ^ 1 P ^f z I P '^{( R a} x ) Х г ⁽ у , z ) ⁺ V 2 d 2 ) V R )

+——

R 2 ^{e - a}

P ^{( Ra}У M ^Rax^)дП^Х_£ ⁽ у , ^z ) ⁺ ^yy ^sin d x           4 d 2

(i

+ "i^ MR ^a У ^{)) 2} n +

R

т f П у I ₂f z I cos ² —— I P ² | — l +

V 2 d 2 )  V R )

^{Х £} ) ) +

n

⁺ d 2 R ^e-a

sin

( n d

f П У I f z I cos 4TJp|Ip(RУ)n(x,z)+

V 2 d 2 ) V R )

+

n .

+----sin d.R e

¹ nx ) Id. J cos

V uiJ

—I p (R - x )& p l L J + V 2 d ₂ J        5 y V R J

—— p' ( R a y ) p ( R a x ) n ( x , z ) — ^— + —sin ²   J sin ²   J p{^— J | ^{2 e-a V} ’ ^A , ’ Уy R² V 2 d 1 J V 2 d 2Л V R JJ

+

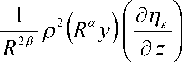
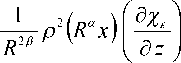
2 sin

R 1 + ^:

¹ nx Id ^J

V^^wi J

I n y I / z I / \ d n 2 .

I p ' — p ( R ^a y ) — ^— +     sin

V 2 d ₂ J   V R J        d z   R 1 + ^e

¹ nx Id ^J

V ^ui J

' n y )

_V 2 d ₂ ^Jx

x p '[ z 1 p ( R ^a x ⁾ X +² p ( Ry ⁾ p ⁽ R ^a x ⁾

V R J       d z R p дП 9Z— d z d z

Предположим, что препятствие B принадлежит множеству

{( x , y , z ) e Q 0 : | z | <  R }. Введем обозначения для интегралов из (12).

Ii =№ к Гd“ • 12=Ш1^ Гdfi •(15)

n g n

Представим их в виде:

11=]L Bi,(16)

i = 1

12 =£ Aj,(17)

j = 1

где В, - соответствующий интеграл от i-го слагаемого в правой части формулы (13), Aj - соответствующий интеграл от j-го слагаемого в правой части формулы (14). Тогда

Л221 - Л =Л2П У В -У A. = |Л2ПВ. - A - A, - A. 1+ 0 1 2         0            i                 j          0 1 17 13

V i = 1 J j = 1

6               18                                                             618

+л; I S в , I- S A j =- d i d ² J ( p v ) ) ² d r +Л 0 | s в , I- S A , . о»)

V i = 2 J j = 2               ^{4 R} 1 _T l < 2                       V i = 2 J j = 2

j * 7,13                          ^{1 1}                                                     j * 7,13

Введем обозначения

X^a = В ₂ n K a , Y a = B 1 n K a , D — , a = D — n K a ( i = 1,2).

Оценим остальные слагаемые в правой части формулы (18) при

R —^ +^ :

1    2 R ^a

^B 2 = 1рв I p ^{2 ( R -} у ) dy JJ ⁿ 2 ^{( x} , ^z ) ^dxdz = R 0              X^a

12,                                     I 1 I

-2 e + - J p ^{( t} ) d r JJ n_£ ⁽ x , z ) dxdz = O I -2e+- I ,

^R 0          X a                V ^R J

1 2 R a

B 3 = Т2 У J p ^{2 (} R a x ) dx JJ x E ⁽y , z ) dydz =

R 0               Y^a

1 ²2                                          ( 1 A

=_u a J p ^{( T} ) ^{d T} JJ X e ⁽ y , z ) dydz = O I -^вт I ,

R 0           Ya                  V R    J

B 4 =

~ 2 R - a

J P ^{( R} “ У ^)sin

R ₀

n y I dy JJ si

.    2 J      X^a

■ n x I , sin --- П_Е ( x , z ) dxdz =

V 2 d I J

B 5 =

V

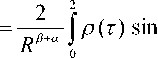
ПТ

V 2 d ₂ R a

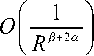
2 R

>- a

d T JJ sin

Xa

П_Е ( x , z ) dxdz

9 2 R        (I

J p ²⁽ R ^a x ^)sin ^-1 dx JJ ^si

R 0                ( ² d 1 J     Y^a

n y I sin — IXe (y, z)dydz = ( 2 d 2 J

(—

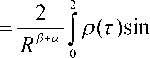
( 2 d 1 R ^a

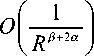
2        , . , .

B 6 <— ^( X^a )^( Y^a ) R

Y

(^{2 R}, - ^a ,     x Y

J p ( R ^a x dx

V 0 J

sin

( n y I

I X e ⁽ y , z ) dydz = ( 2 d ₂ J

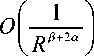
так как n_E , X_E <  1 на X^a и Y^a соответственно.

1 2Rr-a ,           .       (dn          I2.

A 2 =^7" f P ^{( R} y ) dy JI I Я ⁽ x , z ) I ^dxdz = ^e

R 0               n2,a V dxJ

D E

1    22             ,,(dn        I2

= —rR— fp2(t)dT ff —E(x,z) dxdz = O —-— ,(24)

R в+a 0          JJaVdА           V R2 e+a J ,

D E

2 R - a

A 3 = „2 в - 2 a J ⁽ p ' ^{( R a} x ))^{2 dx} JJ X E ⁽ y , ^z ) dydz =

^R        R - ^a                  Y^a

1                  \2                                    ( 1 I

= -72 e - a J ⁽ p ^{( T} ) ) ^{d T} JJ X e ⁽ y , z ) dydz = ^O I -^ e - a I ,                     ⁽²⁵⁾

R 1              Y a                   V R J

2R-a n a       n y I n x I dn I

A =---- 7-     p ( R y )sin ---- I dy cos --- I ^E I dxdz =

4   d 1 Re  J0   V         V 2 d 2 Jy JJ    V 2 d 1 JV dx J п ПТ I П x I dn I ( 1 I

=--- 5— p(T )sin ----- I d T   cos --- I — ^E I dxdz = O ——— , (26)

d 1 R ^{e + a} J    ’ I 2 d ₂ R ^a       JJ a    I 2 d 1 A d x J           V R ^{e + 2 a} J , ^{V 7}

X        /    DE      X xx X

A 5 =

п

2 R

>-<

- a

г

d 1 R ^e-a

cos

R

- a

п x I        •

---I dx   sm

2/7      JJ

V 1 )     Y a

f п v I

I X ( v , z ) dvdz =

V ² d 2 )

п dr

^x JJ sin

Ya

I ^A б| <

- 1 + 2 sin ²

f—I+

V 4 d 1 R ^a )

п

2 d 1 R ^a

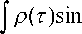
f пт I , --------I d T

V 2 d 1 R ^a )

f п v I

I X ( v, ^z ) ^dvdz , V ^{2 d} 2 )

2 в -a

2 R

-

- a

J P ( R a v ) dv

d|- a l { x e [ R

) - a

,2 R ^{- a} ] }

ypR ^a x ) о x

dxdz = O

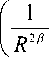
2 R

A = -yar J (p,(Rav)) dv JJn(x,z)dxdz = R      R-a

= "yra Jp(T)) dT JJ n(x,z)dxdz = OI Гвх I,

R 1            xa

—a                        /\ 2

2 R

A = _w J p ² ( R ^a x)dx JJ - X ^- ! dvdz =

^R 0            Dp V ' У )

12             f dx I2

= —— f р(т) dT ff —- I dvdz = O —— ,(30)

R ^{в+a J} ₀          D J V d v ) V R ^в+a )

п

¹⁰    d ₂ R ^{e - a}

2 R - a

r

J P' (R ^a v )cos ПL

- a              2 d

R

a

V

I dv JJ sin X^a

^{п x I} _ / XT 1 — I n - ( x , z ) dxdz =

V ² d 1 )

п d i R ^

- 1 + 2sin ²

п I п

---------1 +---------

V 4 d ₂ R ^a ) 2 d ₂ R ^a ₁

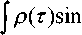
^f пт V

--------I d T

V 2 d ₂ R ^a )

x

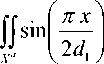
p_E ( x , z ) dxdz ,

2 R - a

A 11 =

п d 2 R в

J p (R ^a x )sin ^x- I dx Jj cos 0                 V 2 d 1 )     Y aa

V

y y l^⁽ v , ^z ) ^dv^dz = 2 d ₂ ) d v

п d 2 Re+a

fр(т)sin ------IdT ffcos —v I   -(v,z)dvdz = O|

J0  V ’   V 2d 1 Ra )    JJ    V 2d2) dvVУ              V Re

2 2 Rr a                          dxf

\A_u <—77;— [ P (Rx ) dx    ff     —^- p ( R v ) dvdz = O ——

¹²l    D^{2 в-a}                                       n

R 0               D-ai{ve[R-a ,2R-a ]} dvV x d - a                      /       \ 2x

A 1. = X2 7 J P 2 ( R a v ) dv JJ " П Н dxdz = O 1^ I ,

R 0            D2,aV dz V          V RV

i d - a                      / X 2               /\

If,И I

A 15 = P ? I p ² ( R x ) dx II -£\ dydz = O I"^ 1 •

^R 0            D V a V ^{d Z} ) V ^R )

A 16 = A 17 = 0, так как supp p'(z / R ) n B = 0 ,

^ 2 R a            2 R a

I A 18|⁵.      I p ( R a y ) dy I p ( ^{R a} x ) dx = O I _: I ^.

R 0           0

Потребуем, чтобы выполнялась система неравенств

1 >  в >  1/2, в + 2 a >  1, 2 в + a >  Ц

2в-а > 1, a > 0.

Отсюда наибольший вклад в асимптотику Л2011 -12 при R ^ +да дают слагаемые с А5 и А10. Пусть α = 0,4 и β = 0,7.

Тогда справедливо асимптотическое представление

Г

Л 1 1 -

- П 1 . nx

I₂ =      -- sin ---

² R °'⁷I d ₂W    I 2 d

2 X             1

■ V ( x , Z ) dxdz + 1 [[sin 4 4 I X ( У , z ) dyd

)                d 1 "     V 2 d ₂ )

z

V

I ^

+ O ( R *) при R >-t ,                                        (38)

из которого следует выполнение неравенства (12). Теорема доказана. ■

Применим вариационный метод для случая бесконечно тонкого плоского препятствия, протяженного вдоль оси волновода. Пусть B есть бесконечно тонкая пластина ненулевой площади с кусочно-гладкой границей, расположенная в плоскости y = 0.

Введем обозначения

Q up = { ( x , y , z ) 6^ 0 : y >  0 } .

Рассмотрим сужение задачи (2) на половину волновода Q up up

( А + Л ) u^up = 0 в Q up , ---- = 0 на 50 up \ X , u^up = 0 на X .      (39)

5 n

Имеет место утверждение, аналогичное лемме 1, где Л ² ₀ = п ² /4 d ₂ ² -точка отсечки непрерывного спектра задачи (39), H 0 - пространство Соболева, полученное замыканием в полунорме (12), где Q a надо заменить на Q ^up , подмножества класса бесконечно дифференцируемых функций в Q up , удовлетворяющих условиям:

а’) функция u (x, y, z) = 0 для (x, y, z) 6 X, б‘) носитель u(x, y, z) ограничен в Qup .

Справедлива

Теорема 2. Пусть B - бесконечно тонкая пластина ненулевой площади с достаточно гладкой границей , расположенная в полосе { ( x , y , z ) 6 Q ₀: y = 0 } . Тогда существует наименьшее собственное значение задачи (2) , которое принадлежит интервалу (0, п 2 /4 d ₂²) .

Доказательство. Пусть s >  0, D _E - множество на плоскости Oxz

De ={ (x ,0, z) e B: dist ((x ,0, z), 5B) < £ }, %E (x, z) - достаточно гладкая функция, такая, что

X ( x, z ) = 1, если ( x ,0, z ) e B \ D _E , X ( x , z ) = 0, если ( x ,0, z ) e X , 0 <  x_£ ( x , z ) <  1, если ( x ,0, z ) e D _£ .

В качестве пробной функции можно выбрать

V ( x , У , z ) = sin

z A 1

О    P ( RУ ) X ( x , z ),

V R ) R

где функции p и x_£ определены формулами (16) и (40). Вычисления, подобные тому, какие были проведены в теореме 1, показывают, что справедливо представление

^ 7JJJ | ^ |² d Q- JJJ |v V‘ d П = - П .JJ Х £ ( x , .• ) dxdz + О ( ^R -')     (42)

• ⁴ d 2 n uP             n uP                 d 2 ^R     B

для достаточно большого R и достаточно малого фиксированного £ >  0, из которого следует утверждение теоремы. ■

Замечание. Рассмотрим случай волновода без препятствий. Известно [5], что в цилиндрическом волноводе задача Неймана (2) при B = 0 не имеет собственных значений. Пусть теперь волноводная область n является кусочно-гладким локальным возмущением области П ₀, таким, что выполняются условия:

• а)    П ₀ с n и 0 < mes ₃ ( n \ П ₀) <  да ;

• б)    существует r > 0 такое, что n \ n ( r ) = Q ₀\ n ₀( r );

• в)    d ( n \ n 0 ) ndn 0 с (({ у = d ₂ } и { у = - d ₂ }) n д n ₀ ) ;

• г)    n n { у = 0 } с П ₀;

• д)    П симметрично относительно плоскости у = 0.

Тогда существует собственная функция задачи (2), нечетная по переменной у, и соответствующее собственное значение принадлежит интервалу (0, п2/4d22). Для доказательства достаточно рассмотреть в качестве пробной функцию

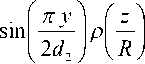
для ( x , у , z ) en up ,

f ^ ( x , У , z ) = ^

_ 1, для ( x , у , z ) en up \ n u .

Тогда справедливо представление

^— J| v 12 ^{dx -} J| ^v V 12 ^dx = T ^ y ^mes 3 ^{( n} \ ⁿ 0 ) ^- A ,

• ⁴ d 2 n 0 p         n 0 p              ⁸ d 2                    ^R

где А - положительная постоянная, не зависящая от R. Из формулы (44) следует существование наименьшего собственного значения рассматриваемой задачи в интервале (0, п 2/4d22). Отсюда вытекает, что для любого локального возмущения Ω \ Ω0 области Ω0, где область Ω удовлетворяет условиям а) - д), существуют собственные значения задачи (2), погруженные в непрерывный спектр.