Об управлении одной системой второго порядка в сопротивляющейся среде

Рассматривается задача о переводе начального состояния линейной системы второго порядка в начало координат в течение заданного времени. Управление ограничено по модулю, минимизируется функционал энергетических затрат. Исследуемая система описывает управляемое движение материального объекта (тела) в сопротивляющейся среде. В данной постановке, при условиях, что величина управления не ограничена и отсутствует сопротивление среды, задача исследовалась в работах [1; 2].

В статье для решения рассматриваемой задачи используется принцип максимума Л.С. Понтрягина [3]. Приводятся результаты решения с учетом и без учета сопротивления среды краевой задачи принципа максимума. Построены оптимальные законы изменения управления, определены фазовые траектории, найдены минимальные значения энергозатрат при перемещении объекта.

1.    Постановка задачи оптимального управления

Рассматривается задача оптимального управления движением объекта, подверженного действию сил сопротивления. Предполагается, что сила сопротивления пропорциональна скорости движения тела. Обозначим через x(t) - координату, определяющую положение объекта, а через u (t) - управляющую силу, ограниченную по модулю. Движение объекта описывается дифференциальным уравнением второго порядка вида x + kx = u,                  (1)

где k – положительная постоянная. Без ограничения общности считаем, что дано тело единичной массы, а управление u ( t ) удовлетворяет ограничению

| u ( t )| ^ 1 .                            (2)

Требуется найти управление u ( t ) , переводящее систему (1) из начального состояния

x ( 0 ) = x ₀ >  0, х( 0 ) = 0           (3)

в конечное положение

x ( T ) = x ( T ) = 0              (4)

т = 2 4x 0 ,

и минимизирующее функционал энергетических затрат

T

J = - J u² dt ,                (5)

где время перехода T задано.

Отметим, что к соотношениям (1)–(4) сводятся также задачи оптимального управления переориентацией сферически симметрично твердого тела в сопротивляющейся среде [4].

• 2.    Применение принципа максимума

Воспользуемся принципом максимума Л.С. Понтрягина [3]. Определим фазовые координаты при помощи соотношений x1 = x, x2 = x и преобразуем уравнение (1) к виду xi _ x2, x2 = — kx 2 + U.

Введем сопряженные переменные ψ ₁ , ψ ₂ и константу ψ ₀ , соответствующие фазовым координатам x ₁, x ₂ и функционалу (5). Составим функцию Гамильтона–Понтрягина

H = — 0 ₀ u +1 / 1 x ₂ - ку ₂ x ₂ + у ₂ u .     (7)

Если у ₀ = 0, то этот случай по форме совпадает с задачей быстродействия, подробно рассмотренной в работе [4]. Тогда оптимальное управление имеет вид

[- 1, 0 <  t <  т , U = <

[+ 1, т <  t <  T .

Время T окончания процесса и момент τ пе-

T т = —

при к = 0.

В этом случае значение функционала (5) равно

Т

J = р             (11)

Пусть теперь у ₀ ^ 0. Из условия максимума функции Гамильтона–Понтрягина (7) следует, что у ₀ <  0.. Без ограничения общности можно положить у ₀ = - 1.

Выпишем сопряженную систему дифференциальных уравнений

JV1 = 0, у 2 = у + ку 2, найдем ее общее решение

У1 = аъ kt 1

у₂ = а₂е + —а_х

и преобразуем функцию H :

H = ^{- 1 ( и -} у 2 ^{) 2} + ¹ у 2 ² + у 1 ^x 2 ^{- к}у 2 x 2 . ⁽¹³⁾

Если при всех t е [ 0, T ]

|у2| < 1,(14)

то функция H достигает максимума, когда и = у 2.(15)

Если при некоторых t е [ 0, T ]

|у2I > 1,(16)

то функция H достигает максимума, когда выражение ( и - у ₂ ) ² будет иметь минимальное значение.

Отдельно рассмотрим эти два случая.

реключения управления определяются из следующих соотношений при к ^ 0 :

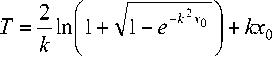
т = 2 ( T + kx 0 )               (9)

• 3.    Построение оптимального решения задачи при условии (14)

Из соотношений (13), (15) следует, что и = a2ekt + 0-а .              (17)

2 k 1

и из выражений:

Подставим выражение (17) в систему дифференциальных уравнений (6) и найдем общее решение этой системы:

,     d^ - kt .    1 kt _ 1

x< — d--e +-- a cec +— at\t ,

1     1 k         2 k 2 2        k 2 1 ,

- kt      1 kt 1

x^ — d^e  + ce +    a, .

2     2        2 k 2 k 2 1

Постоянные a ₁, a ₂, d ₁, d ₂ определим из граничных условий (3), (4):

Найдем условие, при котором реализуется закон изменения управления по формуле (20). Воспользуемся соотношениями (14), (15). Получаем, что начальное значение фазовой координаты x ₀ должно удовлетворять ограничению

- k ³ sh kT

x

2 - 2ch kT + kT sh kT °

_      k ² ( 1 - e - ^kT ) x о

2 - 2ch kT + kT sh kT ’

2 - 2ch kT + kT sh kT x^  -------\-----

⁰        k ² ( ch kT - 1 )

.

,   1 - ch kT + kT sh kT к —-----------------------Xo,

• ¹    2 - 2ch kT + kT sh kT

, =         k ( e ^{kT -} l ) x о

• ²    2 ( 2 - 2ch kT + kT sh kT ) ’

Подставим эти соотношения в систему (18) и преобразуем полученные выражения. Тогда

1 - ch kT + ch kt - ch k ( T - 1 ) x, —------------------------------

• ¹     2 - 2ch kT + kT sh kT

k ( T - 1 ) sh kT

• 2    - 2ch kT + kT sh kT x ^0,

x о ⁺

x ₂ —

k sh kt + k sh k ( T - 1 ) - k sh kT 2 - 2ch kT + kT sh kT

x 0 .

Подставим a ₁, a ₂ в формулу (17) и найдем

управление

u — k²

( 1 - e - ^kT ) e^{k t} - sh kT

2 - 2ch kT + kT sh kTx

а затем – значение функционала энергетических затрат

J —

k ³ x ₀² sh kT

2 ( 2 - 2ch kT + kT sh kT ) ’

Отметим, что из формулы (20) следует,

что управляющая функция u ( t ) монотонно

возрастает от минимального

u ( 0 ) —    k ^{( 1} - ^ch kT ) x 0     <  0

^{v J} 2 - 2ch kT + kT sh kT

значения

до макси-

мального значения

u ( T ) —

k ² ( ch kT - 1 ) x о    >  0

2 - 2ch kT + kT sh kT    '

Из соотношений (11), (21) и (22) следует, что значение функционала, вычисляемое по формуле (21), меньше, чем значение функционала, вычисляемого по формуле (12). Таким образом, управление (20) единственно и удовлетворяет необходимым условиям принципа максимума. Поскольку теорема существования оптимального управления [1; 2] применима к данной задаче, то найденное управление является оптимальным.

Соотношения (19)–(21) описывают решение задачи оптимального по расходу энергии управления перемещением объекта в сопротивляющейся среде. Найдем частное решение рассматриваемой задачи для случая, когда сопротивление среды отсутствует. Вычислим в формулах (19)–(22) пределы функций при k ^ 0. Раскрывая неопределенности по правилу Лопиталя получаем, что если x0 удовлетворяет условию x0 - —,             (23)

то оптимальные фазовые траектории и управляющая функция имеют вид

x 1 ^— T 3 x 0 t   T 2 x 0 t ⁺ x 0 ,

6     2 6

^x 2 ^— T T x 0 t ^- TT x 0 t ,

12      6

^— T T x 0 t T 2 x 0 ,

а минимальное значение функционала качества равно

J — T T x 02 .                 (26)

Пример 1

Рассмотрим задачу оптимального

управления (1)–(5) с учетом и без учета со-

противления среды, для которой выполняются условие (23) при k = 0 и условие (22) при к ^ 0. На рис. 1 представлены график зависимости функции управления от времени и оптимальные траектории на фазовой плоскости при x ₀ = 2,532 , T = 5 , к = 0; 0,8 . Используя соотношения (26), (21), получаем J min = 0,308 при к = 0 и J min = 0,792 при к = 0,8 .

x ₂ =

Х 1 =

tc 2 e kk	- kt + ~ 1
— ( к ~2 e -k 2	kt + 1 ) .

,

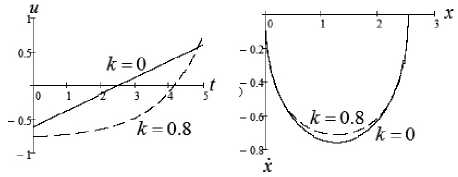
Рис. 1. x ₀ = 2,532 , T = 5

При и = у ₂ фазовые переменные x 1 , x ₂ определяются уравнениями (18). Закон управления и постоянные c ₁, c ₂, c ^~₁, c ^~₂, a ₁, a ₂, d ₁, d ₂ найдем из условий непрерывности функций x 1 ( t ) x 2 ( t ) , и ( t ) в точках переключения и из граничных условий (3), (4). Данным требованиям удовлетворяет управление вида

и = 1

- 1, 0 <  t <  Т 1 ,

2 e^kt - А,

----7----², ^T 1 <  t < ^т 2 ,

А ₁

+ 1, т ₂ <  t <  T .

Фазовые траектории описываются формулами

4. Построение оптимального решения задачи при условии (16)

Если при некоторых t е[0, T] выполняется условие (16), то управление, доставляющее минимум выражению (и - у 2 )2, представимо в виде у2, если |у2I < 1, и = 1

sign у ₂, если | у ₂| >  1.

Из второго равенства системы (12) следует, что функция у ₂ ( t ) является монотонной функцией времени t и поэтому на промежутке [ 0, T ] может менять свой знак не более одного раза. Следовательно, в качестве возможных оптимальных управлений можно рассматривать шесть управляющих последовательностей { у 2 , - 1 } , { у ₂, + 1 } , { - 1, у ₂ } , { + 1, у ₂ } , ^{{- 1, у} 2 ^{, + 1 }} , ^{{+ 1, у} 2 ^{, - 1 }} .

Для отрезка времени, на котором и Е-1, имеем t cl - к/

< X1 =— к " ~ке    C1, x 2 = 1 (kc 2 e ~ kt - 1) .

к

Аналогично, при и е+ 1, получаем

x1 = i

x ₂

1 - е ~^kt k ²

d 1 e ^{- kt}

- t + x 0 , 0 <  t <  Т 1 , k

e ^kt    А

+ 77“---t + d2, T1 < t < T2,(28)

к ² А 1    к А 1

e^{k ( T -} t ) - 1 t - T

P +      ’ ^{т 2} ~t~ ’

¹ e ^kt - 1, 0 <  t <  т , kk   ¹

- kd 1 e ^{- kt}

ekt    А 2

+--- —, т <  t <  т ₂, к А 1    к А 1     ^{1        2}

e ^{k ( T -} t )     1

k k ^,

т ₂ <  t <  T .

Значение функционала (5) равно

J = ¹ ( т + T - т )--^ + ^^-( т - т ) .    ⁽³⁰⁾

2 ^{1        27} к А 1    2 А 2^{и    1}

Из геометрического смысла определенного интеграла следует, что затраты энергии, вычисляемые по формуле (30), ниже, чем затраты энергии по формуле (11).

В соотношениях (27)–(30):

А 1 = e ^{k т 2} - e ^{k т 1}, А ₂ = e ^{k т 2} + e ^{k т 1},

d 1 =

e^{2 к т} 1 + А 1 к ²А 1

, d 2 =

^т 1^(А 2 ^А1 ) к А 1

^{+ x} 0 ⁺ 72". k

Моменты τ ₁ , τ ₂ переключения управления определяются из следующей системы трансцендентных уравнений:

^- 2 t ^{+ X} о ,⁰ < t < ^T 1 ,

2 1 - 3 ( t 2 + т ) t + 6 T 1 1 - 2 т

² x ₀

k τ 2           k τ 1

+ 2 + T = 2 ^e.---kT1e— ek2 - ek

X1 = ‘

6 ^{( т} 2

—

+

, e ^{k 2} + e ^k = e^kT + 1.

Поскольку соотношения (27), (31) определяют управление так же, как и в п. 3, единственным образом, то найденное управление является оптимальным.

Выражения (27)–(32) справедливы, если x ₀ удовлетворяет условию

x ₂

+ ^X 0 , ^T 1 <  t <  T 2 ,

1 2             1     2

_ t ² - Tt + - T ², г 2 <  t < T ,

^- t , ⁰ <  t <  ^T 1 ,

„« Iz k l i k+ l L, т  t <  ' 2 , (37)

^T 2 ^- 7

t - T , т ₂ <  t <  T .

2 - 2ch kT + kT sh kT       2 . ( .к J

------, --------г----< X) < — ln| ch-T I. (33)

k ² ( ch kT - 1 )         0 k ² ( 2 J

Значение функционала качества равно

J=T -

73 T ² -12 X о

.

2 , К k >

Если x₀ = — ln l ch — T I , то время пере- k ² I 2 J

Соотношения (35)–(38) справедливы, если

хода T совпадает с временем T _min в задаче об

T ²

T ²

оптимальном по быстродействию управлении объектом, движение которого описывается соотношениями (1)–(4). В этом случае

— < ^X 0 <— .

τ ₁

= т

₂ = ^{1 (} T + ^kx о )

и минимальное значение

T функционала J = — 2

.

Если x_n = — , то T = T = —T , J = — .

0     4,       1     2 2 , J 2

T ²

Если X _n > —, то 0 4

k = 0 решения не имеет.

задача (1)–(5) при

2 , L k J

При x0 > —lnl ch—T I рассматривае-k \ 2 J мая задача (1)–(5) решения не имеет.

Если сопротивление среды отсутствует, то моменты τ1 , τ2 переключения управления определяются в явном виде и соответственно равны

T - J3T ²-12 X_o      T + J3T ²-12 X_o

Ti = —-----", т2 =--------- (34)

Оптимальное управление и траектории оптимального движения имеют вид u =

- 1, 0 <  t <  T i ,

< 2t-(t2 + T), T1 < t <т2,

T 2 - 7

+ 1, T 2 <  t <  T ,

Пример 2

Рассмотрим задачу оптимального управления (1)–(5) с учетом и без учета сопротивления среды, для которой выполняется условие (39) при k = 0 и условие (33) при k ^ 0. На рис. 2 представлены график зависимости функции управления от времени и оптимальные траектории на фазовой плоскости при X ₀ = 2,532 , T = 3,7 , k = 0; 0,8 . Используя соотношения (34), (38), найдем моменты переключения управления T 1 = 0,216 , т ₂ = 3,484 и минимальное значение функционала энергетических затрат J _min = 0,760 при k = 0, а по формулам (32), (30) вычислим моменты переключения управления T = 0,271 , т ₂ = 3,312 и J _min = 1,511 при k = 0,8 . Отметим, что при управлении движением объекта в среде с сопротивлением по сравнению с движением в среде без сопротивления увеличились промежутки [ 0, т 1 ] , [ т ₂, T ]

времени движения с максимальным по модулю значением управления и уменьшился промежуток времени [ т 1 ,т 2 ] , при этом затраты энергии возросли почти вдвое.

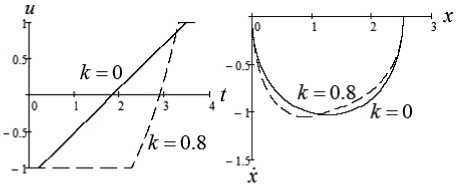
Рис. 2. x 0 = 2,532 , T = 3,7

Пример 3

Рассмотрим задачу оптимального управления (1)–(5) с учетом и без учета сопротивления среды, для случая, когда заданное время перехода совпадает с минимальным временем, при котором еще возможен переход из начального состояния (3) в конечное положение (4). Тогда управление u ( t ) является кусочно-постоянной функцией и имеет одно переключение. Момент переключения вычисляется по формулам (9), (10), а минимальное значение функционала – по формуле (11).

На рис. 3 представлены график зависимости функции управления от времени и оптимальные траектории на фазовой плоскости, когда x 0 = 2,532 .

При k = 0: T = 3,182 , т = 1,591 , J min = 1,591 ; при k = 0,8 : T = 3,625 , т = 2,825 , J min = 1,813 .

Заключение