Обеспечение устойчивости программного движения электромеханического манипулятора

Для изучения динамики манипуляционных роботов, определения конструктивных параметров и законов управления необходимо иметь расчетные механические модели, с достаточной точностью описывающие свойства реальных роботов. Выбор расчетной модели в каждом случае обусловлен кинематической схемой манипулятора, механическими свойствами (инерционными, упругими, диссипативными и т.п.) его деталей и узлов, типом и характеристиками приводов, а также необходимой точностью производимых расчетов.

С математической точки зрения расчетная модель манипуляционного робота представляет собой систему дифференциальных уравнений. Эта модель может содержать уравнения, описывающие также явления немеханической природы, например, электрические процессы в цепях электродвигателей приводов.

Работа выполнена при финансовой поддержке РФФИ, код 10-01-00381.

• 1.    Условия асимптотической устойчивости движения управляемого электромеханического манипулятора

Поставим задачу нахождения условий , обеспечивающих асимптотическую устойчивость программного движения электромеханических систем с голономными и неголо-номными связями.

Для электродвигателя постоянного тока с независимым возбуждением выполняются соотношения [1]

L d ^ + R *^ + k ² n *ф = ku ,     (1.1)

dt

M * =- n *ц — 10 n *'Ф ,          (1.2)

где (p - угол поворота ведомой шестерни редуктора; n * – передаточное число редуктора (отношение числа зубьев ведомой и ведущей шестерен); L* и R* – соответственно коэффициент индуктивности и электрическое (омическое) сопротивление обмотки ротора электродвигателя; u – управляющее электрическое напряжение; ^ - момент электромагнитных сил, создаваемых двигателем и приложенных к его ротору; I – суммарный момент инерции ротора электродвигателя и ведущей шестерни редуктора относительно оси вращения; M * – момент сил реакции, дейст- вующих на ведущую шестерню; k - коэффициент, зависящий от напряжения на входе цепи возбуждения. Предположим, что это напряжение постоянно. Тогда k = const.

При описании динамики манипуляционных роботов обычно используют уравнения Лагранжа второго рода:

d (д L ^   дL    *

—I    I--= M .

dt ^ д q )  д q

(1.3)

Уравнения (1.1), (1.2) описывают электрические процессы, проходящие в электродвигателе звена манипулятора; (1.3) - динамику звена манипулятора. Аналогичные уравнения можно составить для каждого звена. Уравнения типа (1.1), (1.2), (1.3) можно объединить в систему [2]:

d q

=q, dt

— = M 4 (— n * u — Y \ dt

(1.4)

d u

, dt

—

*                *

R _ k2 n     k _

* u +— q + ~u u . LLL

Заданной программой движения манипуляционной системы можно считать ограничения, наложенные на обобщенные координаты и скорости, которые в общем виде можно представить как совокупность уравнений го-лономных и неголономных связей:

f ( q , t ) = 0,        f '( q , q , t ) = 0,     (1.5)

В [3] было показано, что для обеспечения асимптотической устойчивости интегрального многообразия Q ( t ), описываемого уравнениями (1.5), следует использовать вместо уравнений связей (1.5) уравнения программных связей:

f (q, t) = a, f (q, q, t) = a,

< f '( q , q , t ) = a ',                    (1.6)

^{f (}^ q , q , t ) = a ,

-,^

I f ( q , q , q , t ) = a .

в которых возмущения связей a,a,a,a',a' рассматриваются как переменные, удовлетворяющие дифференциальным уравнениям a * i = ^,(a *, q, q, t), .

a i = ^i (a ,a , q, q, q, t), где a * = (a1,..., am, a1,..., am ,a[,..., a'r), ^(0, q, q, t) = 0,        ^ (0,0, q, q, q, t) = 0.

Правые части уравнений (1.7) можно выбрать так, чтобы их тривиальное решение a1 =... = am = a1 =... = am = a1 =... = am = a= = =... = a'r = a ‘ =... = a ‘ = 0 было асимптотически или экспоненциально устойчиво [4]. Будем считать, что из асимптотической или экспоненциальной устойчивости тривиального решения a = oc = a = a' = a '^ 0

уравнений (1.7) следует соответственно асимптотическая или экспоненциальная устойчивость интегрального многообразия Q ( t ).

Подставим вместо q выражение q = Q (q, q, u), полученное из (1.4).Тогда будем иметь f (q, t) = a, f (q, q, t) = a,

“ ^{f (} q , q , t ) = ^a , f ( q , q , u , t ) = a , -

, f ‘ ( q , q , u , t ) = a ‘ .

(1.8)

Уравнения (1.7) подбираем так, чтобы они удовлетворяли системе дифференциальных уравнений:

Г

---= Aja + A 2a + A 3a + A 4a' + A 5a', dt,                                           (1.9)

A1 -/  A2A2a'  A2-c'

— A1 a + a 2 a + a з a + a 4 a + a 5 a , где матрицы имеют размерности: A 1, A1, A2 -(mxm), A3,A4 - (mxr), A02,A2,A2 - (rxm), A3!, A4 - (rxr) - и состоят из коэффициентов, которые подбираются исходя из условий асимптотической устойчивости движения.

Рассмотрим более подробно поиск коэффициентов (матриц коэффициентов) A j i = 1,2, j = 1,...,5 из (1.9), которые подбираются из условий асимптотической устойчивости движения.

Введем обозначения:

g =

' a'

a

a

a k a '7

, g =

7 — 7

a

a a a'

k a'z

,

A =

( о

0 Л

2 V = a - B - a + 2a - C - a + 2a - D - a +

+ a - E - a + a - G - a + 2a - F - a +      (1.14)

+ a T - K - a + 2a T - L - a + a T - M - a ,

где B,C,D,E,F,G,K,L,M – симметрические матрицы с постоянными коэффициентами. Сравнивая правые части в выражениях (1.12), (1.13), (1.14) для функций V , получим

0 A ;

A ²

k A 1

^A 2 ¹ 0

^A 2 ²

^A 3 ¹ 0

^A 3 ²

¹ A ₄

² A ₄

A 5

A ²

A 5 7

.  (1.10)

Можно записать уравнения (1.9) в виде

	' B	C	D	0	0 "I
	C	E	F	0	0
R =	D	F	G	0	0
	0	0	0	K	L
	k 0	0	0	L	m 7

(1.15)

g = A ^- g ,

(1.11)

где в матрице A на соответствующих местах находятся соответствующие блок-матрицы.

Функцию Ляпунова представим в виде

2V = gT • R • g,

(1.12)

Таким образом, R 11 = B , R ₁₂ = R ₂₁ = C ,

R ₁₃ = R ₃₁ = D ,      R₂₂ = E ,      R ₂₃ = R ₃₂ = F ,

R33 = G, R44 = K,  R45 = R54 = L,  R55 = M, остальные R,, = 0 . ij

Найдем производную V V . Для этого продифференцируем выражение (1.14). Полу-

где R =

( ^R 11

...

k ^R 51

... ^R 15

...      ...

...

^R 55 >

чим

,

R = R^T ,     R₉ ,

i , j = 1,...,5 - блок-матрицы размерностей.

соответствующих

Так как векторы a,a,a,a',a' и матрицы  Rj, i, j = 1,...,5 состоят из скалярных функций и Rij = RT, то будут выполняться равенства  aT - R„ a = a'T - Rh-a . Отсюда ij                           ji

следует, что

a • R -a + a^T • R„ -a = 2a^T • R -a' . ij                              ji                              ij

Перепишем функцию Ляпунова (1.12) учетом изложенного:

с

^ТГ —T     — . —T      — . —T.

2V = a - Rn - a + or - R22 - a + or - R33

+ a - R44 - a + a  - R55 - a + 2a  - R12

+ 2aT - R13 - a + 2aT - R14 - a' + aT - R15 -

TT

+ 2a - R23 - a + 2a - R24 - a +

+ 2a T - R25 - a + 2a T - R34 - a +

+ a - R35 - a + 2a - R45 - a .

(1.13)

Будем искать функцию Ляпунова V в виде [5]

V = a - B - a + a - C - a + a - C - a +

TTT

+ a1 - D - a + a1 - D - a + a1 - E - a +

+ aT - F - a + aT - F - a + aT - G - a +     (1.16)

+ a - K - a + a - L - a + a - L - a +

+ a - M - a .

Подставим в (1.16) вместо а и a ‘ выражения из (1.9):

V = а - B - а + а - C - а + а - C - а +

a - D - a + +a - D - (A ос + A2 ос + A3 ос +

+ A4a + A5a ) + a - E - a + a - F - a +

+ a ^T - F - ( A [ a + A [a + A^a + A 1a' + A¹^ ') +

+ a ^T - G - ( A a + A la + A 3a + A 1 a' + Aa ') +

+ a - K - a + a - L - a +

+ a - L - ( A 1 a + A 2 a + A 3 a + A 4 a + A 5 a ) +

+ a ' - M - A2a + A2a + A3a + A2a + A52a \

(1.17)

Производная от функции Ляпунова V имеет структуру вида

V = gT - H - g.         (1.18)

Распишем подробнее (1.18):

• V T кT ciT CAT a 'Tk la , a , a , a , a    X H11  H12  H13  H14  H15 1 ' a I H21  H22  H23  H24  H25 a X H 31  H 32  H 33  H 34  H 35 • a — H 41  H 42  H 43  H 44  H 45 a' xH51  H52  H53  H54  H55 ) a ) t — T rr   — T ГГ    — T ГГ   —tT ГГ

— (a ■ H 11 + a ■ H 21 + a ■ H 31 + a ■ H 41 +

где

( B

2 V 1 — ( a T a T a ^T )• C

C

E

F

D "

F

G _y

(“ 'I a .

a >

+ a ■ H51) ■ a + (a ■ H12 + a ■ H22 +

— T TT    — tT TT    —tT TT X —

+ a  ■ H^2+ a  • H^2+ a  ■ H^2)■ a +

C — T         — T -rr — T -rr —tT -rr

+ (a ■ H13 + a ■ H23 + a • H33 + a  • H43 +

— tT TT x      , — T rr — T rr

+ a ■ H^2)• a + (a  • H^ 4 +a ■ H24 +

(1.19)

I ^D

2 V 2	TT — ( a  , a	) •[ K L H I L M ){	a 'I ,
			a )
V 1 —(a	, a T, a )
' DA 11	b + da 1	C + DA 1	I	2 a'
fa	C + FA 1	E + D + FA 1		a
GA 11 \      1	GA 2 1	F + GA 1	)	x a >

— T rr     —tT rr —tT rr X —t

+ a ■ H34 ++a  ■ H44 + a • H54) • a + z-T rr — T rr — T rr -tT rr

+ (a  ■ H^ ^ + a ■ H25+ a  ■ H^ 5+ a  ■ H^^ +

— tT rr X — t

+ a   ■ H^ 2) • a .

Перегруппируем слагаемые в выражении (1.17) к виду (1.19), тогда получаем вид матрицы Н :

H —

" DA 1	B + DA	C + DA 1	DA 41	DA\ i
FA	C + FA 1	E + D + FA 1	FA 41	FA 1
GA	GA 2 1	F + GA 1	GA 41	ga 5
LA?	LA 2	LA 2	LA 42	k + la5 2
x MA 2	MA 2	MA 2	MA 4 2	L + MA5 2 )

(1.20)

Рассмотрим случай, когда

A 4 — 0, a 5 — 0, A 12 — 0, a 22 — 0, a 32 — 0.  (1.21)

Тогда матрица Н будет иметь вид

H —
^ DA 1	B + DA \	C + DA■	0	0     ।
fa 1	C + FA 1	E + D + FA 11	0	0
gA	GA 2 1	F + GA 11	0	0
0	0	0	LA 42	K + LA5 2
^ 0	0	0	MA 42	L + MA 2 )

(1.22)

Функцию Ляпунова V и ее производную

V можно записать еще так:

V — V ( a , a ", a , a '.a ') — V₁ ( aa , a ) + V 2 ( a ',a ') , V — V ( a , a , a , a ',a ') — V 1 ( a , a , a ) + V₂ ( a ',a ' ) ,

V 2 — (a ' T , 0 c' ^T ) •

f LA 4   K + LA

X MA 4 L + MA

( a' 4

(1.23)

< a )

По теореме Ляпунова об асимптотической устойчивости будем добиваться положительной определенности функции V и отрицательной определенности функции V . Это эквивалентно требованию положительной определенности матрицы R и отрицательной определенности матрицы H .

• 1)    Положительная определенность матрицы R : главные миноры матрицы R удовлетворяют условию

A_;( R ) >  0, i — 1,...,2 m + r . (1.24)

• 2)    Отрицательная определенность матрицы H : главные миноры матрицы H удовлетворяют условию

• 2.    Исследование условий асимптотической устойчивости движения трехзвенного управляемого электромеханического манипулятора

A, ( H ) <  0 , i - нечетное, i e [1;2 m + r ],

A j ( H ) >  0, j - четное, j e [1;2 m + r ]. (1.25)

Таким образом, мы будем иметь 2(2 m + r ) условий (1.24), (1.25) типа неравенств, наложенных на искомые коэффициенты матриц A j , i — 1,2, j — 1,...,5, и на коэффициенты матриц B,C,D,E,F,G,K,L,M .

В общем случае условий (1.24), (1.25) недостаточно для однозначного нахождения коэффициентов матриц Aⁱ . Поэтому при решении конкретных задач произвольно выберем постоянные коэффициенты матриц B,C,D,E,F,G,K,L,M , а также используем дополнительные условия задачи.

Найдем коэффициенты матриц Aⁱ_j , обеспечивающих асимптотическую устойчивость движения, в задаче попадания схвата трехзвенного электромеханического манипулятора из произвольной точки X ( x , y ) рабочей зоны – полуплоскость левее прямой x = 6 в точку X ^* (6,5) , минуя препятствие, которое ограничено замкнутой кривой Т : ( x - 3) 2 + ( у - 3) 2 - 1 = 0. К тому же потребуем, чтобы схват манипулятора во время движения был параллелен оси Ox .

Уравнения (1.8) примут вид

f,(q, t ) = a1,

f1( <7, q, t) = a 1,

f2 ( q, q, t) = a 2,

‘ f 3 ( q , q , t ) = a 3 ,               (2.2)

f 1(q, q, Д, t) = an

• •                             ______

• ^f 2⁽ q , q , ^ , t ) = ^a 2

• . f3( q, q, Д, t) = a 3.

Уравнения (1.9) примут вид a — a^ ^a^ + a^ 2^ + ai за^ + a^ 4a +

+ a^^a^ + a^a 2 + a i ^a^ ,

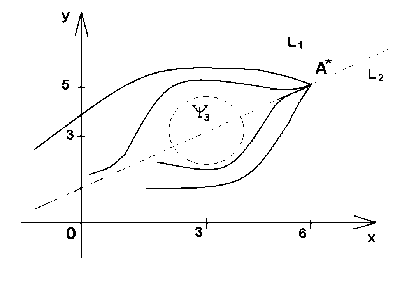
Пример задания ограничения на движение схвата манипулятора

^a 2 = a 21 a + a 22 ^a 1 + a 23 ^a 1 + a 24 ^a 2

+ a₂₅a ₃ + a₂₆a ₂ + a₂-a _;,

+

a₃ — a₃ a + a₃ ac + a₃ a + a₃₄a + L+ a 35 ^a 3 + a 3 ₆ ^a 2 + a 37 ^a 3 .

(2.3)

Связи голономные и неголономные, накладываемые на движения манипулятора, имеют вид [6]

f। е Cos(qi + q2 + q3)-1 = 0, f 2 е x + (x - 6)(1((x - 3)2 + (у - 3)2 -1) +

Уравнения (1.10) примут вид

A —

1 0	1	0	0	0	0	0 1
0	0	1	0	0	0	0
a 11	a 12	a 13	a 14	a 15	a 16	a 17
0	0	0	0	0	0	1
0	0	0	0	0	0	1
a 21	a 22	a 23	a 24	a 25	a 26	a 27
V a 31	a 32	a 33	a 34	a 35	a 36	a 37 j

. (2.4)

+ (у - 3)(2x - 3у + 3)) + 0, f 3 е у + (2x - 3у + 3)Д ((x - 3)2 + (у - 3)2 -1) -

Будем искать функцию Ляпунова V в виде (1.14)

2 v — a • b • a+2a ■ c ■ a3+2a • d • a +

T

+a • e • a+a • f • a+2a • g • a+a • к • a + (2.5)+ 2a'T • L • a' + a'T • M • a',

где, a' —

- 1(( x - 3) ² + ( у - 3) ² - 1)( x - 6) = 0.

(2.1)

a ₂ л

I , b , c , d , e , f, g - постоянные ко-

V ^a 3 J

эффициенты, K —

Ik"  k: 1

V ^Л21   ^л22 J

,

L —

I } l11    1

V l 21    l 22 J

,

где координаты схвата x и y выражаются с использованием кинематики через обобщенные координаты q = ( q 1 , q ₂ , q ₃ ):

Г x = L 1 Cosq 1 + L ₂ Cos ( q 1 + q ₂) + L ₃ Cos ( q 1 + q ₂ + q ₃)

[ у = L 1 Sinq 1 + L ₂ Sin ( q 1 + q ₂) + L ₃ Sin ( q 1 + q ₂ + q ₃).

M —

v

m ₁₁

^m 21

m “ ] m 22 J

– матрицы

с

коэффициентами,     причем

¹ 12 ^{— 1} 21 , m 12 ^— m 21 .

постоянными

k 12 ^{— k} 21 ,

В	уравнении (1.12)	2 V =	gT • R	g ,
матрица R будет иметь вид
	^ b  c  d   0    0	0	0 1
	c  e f  0   0	0	0
	d f g  0   0	0	0
R =	0   0   0    k 11    k 12     1 11		l 12
	0   0   0    k 21    k 22    l 21		l 22
	0   0   0    l 11     l 12     m 11		m 12
	x 0   0   0    l 21     l 22    m 21		m 22 j
	f R  0 1
или	R =    1	.	(2.6)
	1 0   R 2 J

Найдем производную V . Для этого дифференцируем выражение (2.5).

Получим

V = а 1 • b • а1 + а1 • c • а1 + а 1 • c • а 1 + а1 • d • а 1 +

+ а • d • а + а • e • а + а • f • а + а • f • а +

TT

+ a i • g • a i + а • K • а + а • L • а +

(2.7)

+ a T • L • а + a T • M • а .

Подставим в (2.7) вместо а и а' выражения из (2.3). Производная от функции Ляпунова V имеет структуру вида V = gT • H • g , где из (1.20) получаем матри- цу Н вида

H =

f dan	b + dan	c + dal3	dA 1	dA5'   '
fa 11	c + fa 12	e + d + fa 13	fA 4 1	fA 1
ga 11	ga 12	f + ga 13	gA 1 4	gA 5
LA 2	LA 2	LA 2	LA 4 2	K + la5 2
X MA i2	MA 2	MA 2	MA 4 2	L + MA 2 2 ?

(2.8)

Здесь

A 41	=	-( a 14    а и		) ,		A 5 =	( a 16    a 17 ) ,
A 2 =		a 21	, A 22	=		f a 22 1	,	A" =	a 23	1
	X	a 31 j				X a 32 J			X a 33 J
A 42 =		a 24	a 25		,	A 5 =		a 26	a 27
		X a 34	a 35 J					X a 36	a 37 j

Рассмотрим случай, когда

A 1 = 0, A 1 = 0, A 2 = 0, A 22 = 0, A 22 = 0.   (2.9)

Тогда матрица Н будет иметь вид

H =

f da 11	b + dan		г + da13	0	0    1
fa 11	c + fa 12	e + d + fa 13		0	0
ga 11	ga 12	J	r + ga 13	0	0
0	0		0	LA 4 2	K + la5 2
X 0	0		0      MA 2		L + MA5 5 ;
или	H	=	f H 1   01 X 0    h 2 J	.	(2.10)

Функцию Ляпунова V и ее производную V можно записать еще так:

V = V (a, «1,al, a2, a3, a2, d3) = = V (a, aii, ^i) + V2 (a, a3, «2,0*3)

V = V (a, «1, с*, a, a3, a2, a3) =

= V ( a , «1 , *1) + V ₂ ( a ₂, a ₃, d₂, d₃),

	f b   c  d 1		^ a j 1
где 5 V = ( a  «1 a j ) •	cef	•	• a 1
	x d f g J		• • X« 1J

2 V₂ = ( a₂  a₃   a₂ d ₃) x

11      12      11       12		a 2'
к    к     1      J 12   л22    4 2      2 22	•	a 3	(2.11)
1 11     1 12     m 11    m 12		a 2	,
X l 15     l 22    m 12    m 22 J		X *3 3 J

V = ( a «1 a j)x

	f dan	b + da12		c + da^	1	f a			1
x	fa 11	c + fa	12	e + d + fa13		•		al
	x ga 11	ga 12		f + ga 13	J		X	ax	J
						^ a		2
V 5 =( a		5    a 3	a 2	«3 ) • H 2	•	a a		3 5	.
						xa		3 J
			f H 11	H 122    H 123	H 124 1
где	H 2	H 5 =	H 2 2 1 H 321	22 H 22 H 23 22 H 32   H 33	H 2 2 4 H 324			,
			X H 421	H 422   H 423	2 H 44 J

H121

^{— 1} 11 a 24 + ¹ 12 a 34

H122

^{— l} 11 a 25 ^{+ l} 12 a 35

^H 21 ^{— 1} 12 a 24 + ¹ 22 a 34

H 31 = m u a 24 + m 12 a 34

^H 41 ^— m 12 a 24 ⁺ m 22 a 34

H 22 ^{— l} 12 a 25 ^{+ l} 22 a 35

H 32 ^— m 11 a 25 ⁺ m 12 a 35

^H 42 ^— m 12 a 25 ⁺ m 22 a 35

^H 13    ^k 11 ^{+ l}11 a 26 ^{+ l} 12 a 36

H

H

H

H

^{— k} 12 ^{+ l}12 a 26 ^{+ l}22 a 36

^{— l} 11 ⁺ m 11 a 26 ⁺ m 12 a 36

- l 12 + m 12 a 26 + m 22 a 36 ,

H

H

H

• ^{—    k} 12 ^{+ l} 11 a 27 ^{+ l} 12 a 37

• ^{—    k} 22 ^{+ l} 12 a 27 ^{+ l} 22 a 37

• ^{—    l} 12 ⁺ m 11 a 27 ⁺ m 12 a 37

• ^{—    l} 22 ⁺ m 12 a 27 ⁺ m 22 a 37 ^.

Найдем частное решение задачи поиска коэффициентов a , обеспечивающих асимптотическую устойчивость заданного движения манипулятора. Выберем коэффициенты b , c , d , e , f , g :

b = 8, c = 3, d = 2, e = 4, f =1, g =5. (2.14)

Матрица R будет иметь вид

< 8  3  2Л

R 1

12  1

⁵ J

По теореме Ляпунова об асимптотической устойчивости будем добиваться положительной определенности функции V и отрицательной определенности функции V . Это эквивалентно требованию положительной определенности матрицы R и отрицательной определенности матрицы H . Так как V — V + V₂ и V - V + V₂ , будем добиваться положительной и отрицательной определенности квадратичных форм V , V₂ и V , V ₂, имеющих вид (2.11) и содержащих коэффициенты

Условия положительной определенности матрицы R в (2.12) выполняются.

Матрица H будет иметь вид

	2 а ц	8 + 2 a12	3 + 2 a, /
н 1 —	a 11	3 + a12	6 + a „
	v 5 a 11	5 a	1 + 5 a j3y
Пусть   a	— — 3 ,	a 12 — — 2 ,	a 13 — 1.

.

(2.15)

-

a ₁₁ , a ₁₂ , a ₁₃ , a ₂₄ , a ₂₅ , a ₂₆ , a ₂₇ , a ₃₄ , a ₃₅ , a ₃₆ , a ₃₇ .

1) Для положительной определенности квадратичной формы V и отрицательной определенности квадратичной формы V необходима положительная и отрицательная определенность матриц R и H . Из этих условий следует

4( rj > о    Шн 1) < о

< 4 ( R ) >  0 и Ц ( H ) >  0.  (2.12)

4 ( r ) > о    4 (н) < о

Тогда

Условия

H 1

—

—

V

-10

J

.

отрицательной определенности мат-

рицы H в (2.12) выполняются.

Пусть k 11    6, k22    5, k 12    2, 111    1,

l22 — 1, mn — 4, m22 — 3, ll2

Матрица R будет иметь вид

— m_n — 0. (2.16)

2) Для положительной определенности квадратичной формы V и отрицательной определенности квадратичной формы V ₂ необходима положительная и отрицательная определенность матриц R и H . Из этих условий следует

V

А

R 2

6	2	1	0
2	5	0	1
1	0	4	0
0	1	0	3

.

А

J

Условия положительной

определенности мат-

рицы R в (2.13) выполняются.

Матрица H будет иметь вид

'4 ( R 2 ) >  0	'4 ( н 2 ) <  0
4( R 2 ) >  0	4 ( н 2) >  0
и	2    2       .    (2.13)
4 ( R 2 ) >  0	4 ( н 2 ) <  0
! . ( R 2 ) >  0	4 н 2 ) >  0

H 2

a 24	a 25	6 + a^	2 + a22
a 34	a 35	2 + a^	5 + a 37
a 24	4 a 25	1 + 4 a26	4 a 27
V u a 34	3 a 35	3 a 36	1 + 3 a3 7j

.

Пусть

Список литературы д24 = -7, a25 = 0, a26 = -4, a27 = -2,

a₃₄ = 2 , a₃₅ = - 6, a₃₆ = 0, a₃₇ = - 2 .  (2.17)

Условия отрицательной определенности матрицы H в (2.13) выполняются.

Таким образом, мы нашли все искомые коэффициенты aij , i = 1,2,3, j = 1,...,7, при

помощи которых будет обеспечиваться асимптотическая устойчивость заданного движения (2.1) трехзвенного электромеханического манипулятора. В результате матрица коэффи-

циентов a из (2.4) примет вид

—

-

A =

0 >

1  .(2.18)

-

0  — 4  — 2

k

—

0   — 2 J

• 1.    Чиликин М.В., Ключев В.И., Сандлер А.С. Теория автоматизированного электропривода. М.: Энергия, 1979.

• 2.    Соколов А.В. Об управлении движением электромеханического манипулятора // Проблемы механики и управления. Пермь, 2003. Вып. 35. С. 136–151.

• 3.    Мухарлямов Р.Г. Математическое моделирование динамики несвободных механических систем // Вестн. Рос. ун-та дружбы народов. Сер.: Прикл. математика и информатика. 1996. № 1. С.31–37.

• 4.    Мухарлямов Р.Г. О построении множества систем дифференциальных уравнений устойчивого движения по интегральному многообразию // Дифференц. уравнения, 1969. Т. 5, № 4. С. 688–699.

• 5.    Программное движение механических систем / под. ред. А.С.Галиуллина . М., 1971. 158 с.

• 6.    Соколов А.В. Управление программным движением многозвенного манипулятора // Проблемы механики и управления. Пермь, 2002. Вып. 34. С. 76–93.

The stability movement of the electromechanical manipulator