Обобщенная математическая модель транспортной нагрузки внутри городов

Предисловие

Прикладная наука вышла отчасти из экспериментальной и поначалу имела дело с решением конкретных задач, а не разработкой общих теорий [15]. Отметим, что и в градостроительстве необходимо было решать конкретные прикладные задачи, а не создавать общие теории.

На современном этапе набор таких конкретно решаемых посредством математического моделирования задач достаточно широк. Решаются задачи моделирования и оптимизации сложившейся типа расселения с подзадачами [5], [6], [14], [10]. Исследователи моделируют и прогнозируют в сложившихся условиях особенности регионального расселения, с традиционной привязкой к размещению промышленности [2], [3], [7], [8], [9], [11], [12], [13]1, пытаются строить предположения о бу

дущих параметрах и свойства расселения в городах и т. п. населенных пунктах [4].

Однако для планирования особенностей расселения необходимо учитывать его общие закономерности. Так, в [16], [17], [19] посредством простых моделей глобального расселения была определена предельная (в экологическом смысле) численность населения регионов РФ, и указано, что большинство регионов недонаселены, а малая часть перенаселены. В данной работе продолжается анализ особенностей расселения, связанных с перенаселенностью, на основании общих закономерностей городского расселения.

• 2.    Общая модель транспортной нагрузки

Пусть линейный размер города будет равен а, тогда ясно, что его площадь s пропорциональна квадрату линейного размера s~a², и соответственно население b равно произведению площади на среднюю плотность населения b=k 1 ·s, и также пропорционально квадрату линейного размера b~a².

Далее, жителям города необходимо ездить на работу и обратно, средняя длина суммы всех маршрутов будет пропорциональна ½ линейного размера умноженной на население с~½·b·a, при этом учитывается, что половина населения ездит раз в день туда-обратно (трудящиеся), а половина – нет (дети и пенсионеры). Транспортная нагрузка пропорциональна кубу линейного размера, c~a3.

Экологическая нагрузка равна произведению транспортной нагрузки (суммарно длины поездок в день, с) на некий коэффициент загрязнения окружающей среды на 1 км поездки. При этом, даже если используется электротранспорт, энергия для него вырабатывается на ТЭЦ и т. п., загрязняющих среду, само производство и технические обслуживание средств транспорта требует производственных затрат, сопряженных с производством отходов и т. п.²: d=k 2 ·c. Экологическая нагрузка³ пропорциональна кубу линейного размера d~a³ .

Легко увидеть, что транспортная нагрузка растет быстрее населения (в 3-й степени, а население – во 2-й). Тогда становится ясно, что пропускная способность транспортной сети города ограничена – на единицу площади города дороги занимают определенную часть. Площадь дорог растет квадратично от линейного размера, а не кубически, тогда при росте линейного размера города относительная нагрузка на дороги внутри города растет (повышается интенсивность движения до максимально возможной, равной предельной пропускной способности), и при дальнейшем росте интенсивности движения в пиковые часы наблюдается транспортный коллапс, – скорость движения падает – движение по маршруту определенной длины начинает занимать большее время4. Поскольку время движения по маршруту увеличивается (пусть не более чем линейно от увеличивающегося линейного размера города), то тогда, при транспортном коллапсе, дополнительная экологическая нагрузка пропорциональна четвертой степени линейного размера города d2~a4, и общая экологическая нагрузка есть сумма экологической нагрузки d=k2·c и d2~a4, дополнительной: dобщ= k2·c + k3·а4.

Вышеприведенные соображения сведены в табл. 1, в которой показаны параметры имитационной модели.

Таблица 1. Общая модель транспортной нагрузки

Параметр модели	Формула	Коэфф.
Линейный размер	a	условная единица
Площадь	s=a2	простейш. вариант
Население	b=k 1 ·a2	k 1 =10 чел. на ед. площ.
Транспортная нагрузка	с=½·b·a c=½·k 1 ·a3
Экологическая нагрузка (без трансп. коллапса)	d=k 2 ·c d=k 2 ·½·k 1 ·a3	k 2 =10 ед. на ед. тр. нагр.
Экологическая нагрузка с транспортным коллапсом	d общ = d ⋅ k 3 ·a d общ =k 2 ·½·k 1 ·k 3 ·a4	k 3

Коэффициент k3 учета транспортного коллапса определяется из следующих соображений. Обобщенно при нормальном дви- жении площадь, занимаемая движущимся транспортом (с учетом дистанций между транспортными средствами, необходимыми для максимально возможного транспортного потока) Sтрансп меньше чем площадь дорог города Sдорог: Sтрансп < Sдорог.

При этом площадь дорог растет квадратично от линейного размера города Sдо-рог=kдорог·s=kдорог·a2, а площадь, необходимая транспортному потоку, – пропорционально третьей степени:

S

трансп = k трансп

·с= k трансп

·½·k 1 ·a³.

При транспортном коллапсе, обратном положении, когда дорог недостаточно для потока транспорта Sтрансп > Sдорог имеется коэффициент замедления kзамедл (kзамедл>1), равный отношению необходимой и имеющейся пло-

• ²    Даже если речь шла бы о солнечных батареях как источнике энергии, то при их сроке службы в 20 лет необходимо каждый год утилизировать 5 % и 5 % их количества произвести заново (что сопряжено с определенной экологической нагрузкой на окружающую среду), соответственно при сроке службы в 50 лет – 2 % (но такая долговечность пока не достигнута).

• ³    Экологическая нагрузка в данном случае – некий пропорциональный эквивалент от энергетических затрат на транспортирование.

• ⁴    Так называемые "пробки" движения транспорта.

щадей для транспортных потоков, при этом:

k замедл =S трансп /S

(k трансп

дорог

·½·k 1 ·a³)/(k дорог ·a²)

k

замедл

(k трансп

/ k дорог )·½·k 1 ·a,

откуда ясно, что при транспортном коллапсе, росте площадей S трансп и S дорог экологическая нагрузка возрастает пропорционально произведению k замедл на S трансп – т. е. в четвертой степени. Коэффициент k 3 в табл. 1 таков:

• ⁵    Разумея относительно оптимальную планировку дорожной сети.

• 3.    Имитационное моделирование

k 3 =k 2 ·(k трансп / k дорог )·½·k 1 .

Очевидно, что имеется предельный размер города, в котором еще нет транспортного коллапса, однако определение этого размера вне рамок этой работы.

Для наглядной иллюстрации общих закономерностей, сведенных в табл. 1, было проведено имитационное моделирование, с тем отличием, что средняя длина единичного маршрута определялась методом Монте-Карло между двумя точками, случайно распределенными внутри площади города. При этом наихудший случай транспортного коллапса исключался.

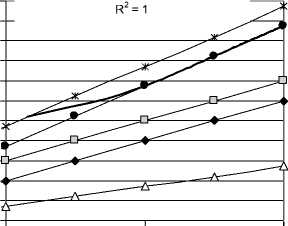
Экологическая нагрузка при этом представлена в виде условной площади города и незаселенных окрестностей вокруг, необходимых для восстановления экологического равновесия, см. рис. 1 и табл. 2.

Таблица 2. Результаты имитационного моделирования

>s Ji CO Ф CL s q 5 CO И О q C к о I ф Ф q q О Ф га I ф Ф s О Q. Ё. В о га E I га Е С я 1 1,0E+00 1,0E+01 0,528 5,28 52,77 3,16 1,0E+01 1,0E+02 1,84 184 1 841 10 1,0E+02 1,0E+03 5,31 5 314 53 141 32 1,0E+03 1,0E+04 16,47 164 709 1 647 089 100 1,0E+04 1,0E+05 51,86 5,2E+06 5,2E+07 316 1,0E+05 1,0E+06 160,2 1,60E+08 1,60E+09 1000 1,0E+06 1,0E+07 480,5 4,80E+09 4,80E+10 y = 5,6674x3 - 283,44x2 + 24994x - 176324

1,0E+11         ^{,           ,}

1,0E+10

1,0E+09

1,0E+08

1,0E+07

1,0E+06

1,0E+05

1,0E+04

1,0E+03

1,0E+02

1,0E+01

1,0E+00

10                100              1000

линейный размер поселения

♦ площадь кол-во населения среднее расстояние

• • транспортная нагрузка

• 4.    Прикладные выводы из модели

площадь экологич.

Полиномиальный (транспортная нагрузка)

Рис. 1. Результаты имитационного моделирования

Из приведенных результатов наглядно видно, что города с бóльшим населением занимают экологически необходимую площадь гораздо (непропорционально) бóльшую, чем сумма площадей городов с меньшим населе-нием6. В связи с этим возникает ряд прикладных задач.

Первая задача: дан город населением 1 млн чел.; сколько населения можно разместить на площади, равной экологической площади восстановления среды для данного города? Исходная экологическая площадь, занимаемая городом в 1 млн чел., – 1,6E+09 усл. ед. площади. Решение приведено в табл. 3.

Таблица 3. Решение первой задачи

	Городов с населением, чел.
Население городов (чел)	10	100	1 000	10 000	100 000
Кол-во городов	3,1E+07	914763	30731	962,5	29,86
Итого населения	3,1E+08	9,1E+07	3,1E+07	9624746	2986420

Как видно из табл. 3, если селить по 100 тыс., то на той же площади выйдет 3 млн чел., а если селить по 10 тыс., то выйдет 10 млн чел. на той же площади что и исходный единственный миллионный город.

Вторая задача: дан город населением 10 млн чел.; сколько населения можно разместить на площади, равной экологической площади восстановления среды для данного города? Исходная экологическая площадь, занимаемая городом в 1 млн чел.,– 5,4E+10 усл. ед. площади. Решение приведено в табл. 4.

Таблица 4. Решение второй задачи

	Городов с населением, чел.
Население городов (чел)	1 000	10 000	100 000	1 000 000
Кол-во городов	1048118	32826	1019	34,1
Итого населения	1E+09	3,3E+08	1E+08	34 105 984

Как видно из табл. 4, если селить по 1 млн, то на той же площади выйдет 30 млн чел.; если селить по 100 тыс, то выйдет 100 млн чел.; а если селить по 10 тыс, то выйдет 300 млн чел. на той же площади, что много- кратно больше, чем при единственном мегаполисе в 10 млн чел.

• 5.    Проверка модели на доступных данных

Естественно, что указанные модели подлежат проверке на действительных данных. Поскольку полных данных не имеется, то проведена частичная проверка, показывающая качественное наличие указанных общих закономерностей модели.

Прежде проверена (по данным Росстата и Росприроднадзора, для регионов России на 2010 г. [22], [21]) экологическая нагрузка образования отходов в зависимости от площади региона и от населения, см. рис. 2, 3.

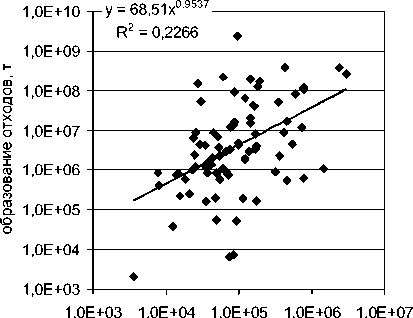
площадь региона, кв. км

Рис. 2. Образование отходов в зависимости от площади региона

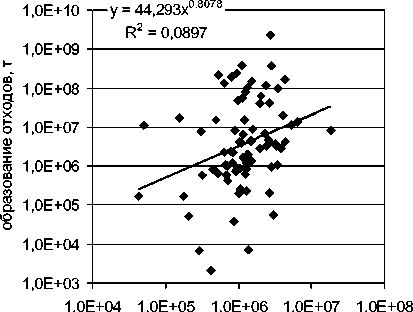
население региона, чел

Рис. 3. Образование отходов в зависимости от населения региона

По рис. 2, 3 видно, что образование отходов зависит (в степенной аппроксимации) от площади и от населения меньше, чем в первой степени, т. е. отходы промышленные и бытовые под закономерность экологической нагрузки, связанной с транспортом, не подпадают, – они описываются линейной зависимостью первой степени.

Во вторую очередь, по меньшей выборке регионов проверена транспортная нагрузка в зависимости от населения региона (данные из [22], [20], на 2010 г. по выборке регионов ЦФО, ПФО и УФО РФ), см. рис. 4, 5. Здесь потребление топлива – это эквивалент транспортной (экологической) нагрузки.

100 000       1 000 000     10 000 000    100 000 000

население, чел.

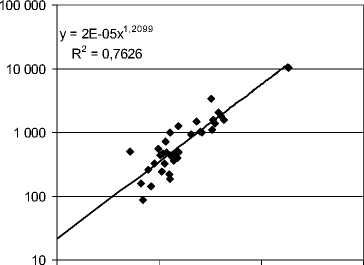
Рис. 4. Эквивалент транспортной (экологической) нагрузки в зависимости от населения региона, для всех регионов выборки

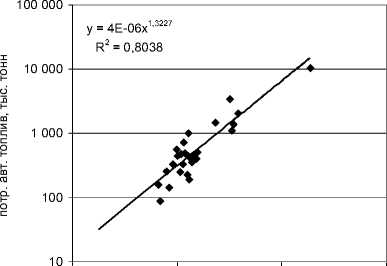
100 000        1 000 000      10 000 000     100 000 000

население, чел.

Рис. 5. Эквивалент транспортной (экологической) нагрузки в зависимости от населения региона, для регионов выборки с площадью до 100 000 кв. км

Хотя регионы не являются плотно заселенными городами, как в исходной теоретической модели, но по рис. 4 видно, что экологическая нагрузка растет в степени большей, чем единица от населения, – функция степенная от населения ~x1,21, причем, если взять выборки для регионов меньшей площади (до 100 тыс. кв. км.), см. рис. 5, то степенная зависимость еще более выражена: функция экологической нагрузки степенная от населения ~x1,32.

Теоретическая же степенная зависимость экологической нагрузки от населения полуторная – ~x1,5 (по табл. 1 ~x3/2).

Приближение с ростом плотности населения степенной зависимости экологической транспортной нагрузки от населения к теоретической величине качественно указывает на проявление основных закономерностей модели в действительности.

Заключение

Таким образом, описаны общие закономерности транспортной, экологической нагрузки городов в зависимости от линейных размеров и населения. Указано, что эти закономерности проявляются на практике. Приведенная модель является основанием для конкретизаций и прикладных использований указанных закономерностей в решении задач планирования расселения.