Обучение учащихся решению олимпиадных задач по математике с помощью теории графов

ле научно-исследовательские труды и учебнометодические пособия. Олимпиадные задачи по предмету, в частности по математике, играют важную роль в процессе работы с одаренными детьми, в первую очередь они способствуют выявлению и развитию одаренности детей в какой-либо научной области. В процессе подготовки к участию в олимпиадах и непосредственно в процессе самого участия формируются навыки научно-исследовательской деятельности учащихся, что способствует саморазвитию и самореализации личности.

Повышенный интерес к проблемам математического образования во всем мире обусловлен ростом значения математики в жизни человеческого общества. Развитие многих наук неразрывно связано с процессами их математизации. К ним относятся не только физика, экономика, информатика, но и современная биология, медицина, лингвистика и пр. Именно поэтому общество нуждается в процессах развития детей, чья одаренность ярко проявляется в математике. Важным средством развития таких детей являются системы олимпиадных задачи по математике.

Проблеме применения олимпиадных задач по математике в развитии учащихся посвящено множество работ, в которых определяется понятие «олимпиадная задача по математике» в соотношении с понятиями «задача повышенной сложности», «нестандартная задача», «задачи на применение нестандартных методов решения», разрабатывается классификация олимпиадных задач; освещается содержание учебных пособий и прошедших олимпиад; рассматриваются вопросы подготовки учащихся к олимпиадам или обучения решению олимпиадных задач и пр. Более подробно остановимся на рассмотрении работ, посвященных различным аспектам вопроса обучения школьников решению олимпиадных задач по математике .

А.Р. Тугузбаева отмечает нацеленность обучения решению олимпиадных задач по математике в 5–6-х классах на освоение приемов умственной деятельности (анализа, синтеза, сравнения и пр.). В качестве основного средства обучения автор приводит упражнения на классификацию, сравнение, абстрагирование, аналогию и др. в рамках реализации принципа Дирихле или метода инвариантов. Именно такие задачи кажутся автору приемлемыми для данной возрастной категории.

А.В. Фарков предлагает осуществлять работу по обучению решению олимпиадных задач по математике на уроке, включая их в системы учебных задач. Например, при изуче- нии квадратных уравнений можно предложить такую задачу: «Может ли дискриминант квадратного уравнения с целыми коэффициентами равняться 2014? А 2016?».

Т.А. Фролова, указывая на несоответствие математических знаний учащихся и требований, выделяет занятия в математическом кружке как одну из форм подготовки учащихся к олимпиадам и отмечает необходимость создания условий для систематизации методов и приемов решения олимпиадных задач; развития исследовательских навыков в работе; систематизации и обобщения знаний; формирования логических навыков в работе; формирования представлений об идеях и методах решения математических задач. Автор рассматривает учебно-исследовательские задания по темам, обучение генерированию идей при решении задач исследовательского характера как основу подготовки учащихся к олимпиадным конкурсам.

А.И. Азаров видит совершенствование методов обучения через формирование у учащихся творческого, эвристического мышления; развитие математической интуиции и навыков самостоятельного поиска закономерностей и взаимосвязей; ознакомление с общими приемами самостоятельного и целенаправленного поиска решения задачи. Автор приводит такие составляющие успеха в олимпиадах по математике, как знание материала школьной программы; знание материала, который выходит за пределы школьной программы; смекалка; гибкость ума; практика; сформированность логико-математических умений (анализ объектов с выделением существенных и несущественных признаков, установление причинноследственных связей в изучаемом круге явлений; классификация условий в задании по некоторому признаку и пр.) и умения строить модели в графической и знако-символьной формах и пр.

И.А. Беловол указывает на то, что при подготовке учащихся к олимпиадам учителю необходимо определиться со стратегией обучения решению нестандартных заданий и задач повышенной сложности. К ним относятся стратегии ускорения (что учитывает потребности и возможности учащихся с различными темпами развития), углубления (за счет более глубокого изучения тем конкретной области знаний), обогащения (за счет нетрадиционных тем и установления связей с другими темами, проблемами или предметами), про-блематизации (предполагает стимулирование личностного развития учащихся с помощью использования проблемных ситуаций, ориги- нальных объяснений, пересмотр имеющихся фактов, поиск новых трактовок и альтернативных интерпретаций). Автор приводит ряд требований к системе подготовки обучающихся к олимпиадам: включение дополнительных тем и актуальных или нерешенных проблем области научных знаний; использование интегрированного подхода к изучению тем и проблем; поощрение углубленного изучения тем, выбранных самим школьником; развитие самостоятельности в обучении; обеспечение гибкости и вариативности образовательного процесса с точки зрения содержания, форм и методов обучения, корректировки методики с учетом специфики индивидуальных особенностей учащихся; обеспечение свободного доступа к разнообразным источникам информации и использование различных способов получения информации.

Е.В. Городнова процесс подготовки учащихся к участию в математических олимпиадах подразделяет на пять этапов: мотивационный, в котором представлены исторические задачи, биографии ученых-математиков, занимательная литература для детей; ориентировочный , содержащий опорную задачу; исполнительный , реализуемый через решение аналогичных задач; контролирующий , осуществляемый посредством решения одной-двух развивающих задач (условия этих задач даются в измененном виде, но сохраняется та же идея решения); последний характеризуется разбором занимательных математических задач, подобранных самими учащимися.

Рассмотрим работы по обучению решению олимпиадных задач с использованием графов .

Е.М. Елисеев видит в переводе условия задачи на математический язык один из основных методов решения олимпиадных задач. В рамках языка теории графов объекты, рассматриваемые в задаче, принимаются за вершины графа, а отношения между ними изображаются ребрами графа. Метод графового моделирования применим на практике, если условие задачи удовлетворяет следующим критериям: существование объектов (любой природы) и отношений между ними, которые можно изобразить вершинами и ребрами графа; комбинаторный характер задачи; возможность изучения структурных связей между объектами. Автор приводит ряд олимпиадных задач, к решению которых можно применить метод графового моделирования.

А.В. Лавренюк представляет двухэтапную модель изучения теории графов при подготовке школьников к олимпиадам по математике. Сначала учащиеся знакомятся со следующими темами теории графов: «История и основные понятия, теоремы теории графов»; «Эйлеров и гамильтонов циклы, задачи о мостах, рисование фигур единым росчерком»; «Лабиринты»; «Раскраска графов»; «Понятия дерева и леса»; «Сетевые графы»; «Применение теории графов в различных областях науки и техники»; «Графы и олимпиадные задачи». Затем приступают к формированию банка олимпиадных задач, решаемых с помощью графов.

Анализ исследований по проблеме применения олимпиадных задач в развитии учащихся позволяет рассматривать системы задач как основное средство подготовки к различным олимпиадам по математике. Авторы приводят аргументы в рассуждениях о роли и значимости данного обучения, но останавливаются лишь на перечислении типов олимпиадных задач по математике или приводят ряд задач (и их решений) одного типа. Несомненно, эти работы вносят весомый вклад в развитие теории задачного обучения с позиции рассмотрения деятельности субъектов образовательного процесса, предполагающей применение системы разнообразных задач и их решений. Однако, рассматривая обучение как подход, при котором учебная деятельность учащихся проектируется и реализуется через решение целесообразно подобранных задач, приведенного выше материала оказывается недостаточно. Нет описания систем задач, которые следовало бы использовать на каждом из этапов обучения решению олимпиадных задач по математике, а в этом и раскрывается сущность за-дачного подхода в обучении учащихся решению олимпиадных задач.

Полученные выводы диктуют необходимость выделения этапов обучения учащихся решению олимпиадных задач по математике и разработки системы целесообразно подобранных задач в соответствии с каждым из них. В ходе подготовки учащихся к олимпиадам по математике используется многообразие задач-ного материала из различных разделов. Как следствие, требуется конкретизация математической области (теория чисел, комбинаторика, теория графов, логика и пр.) при конструировании указанной системы задач. В связи с этим основной целью данной работы является разработка системы целесообразно подобранных задач в соответствии с каждым этапом обучения учащихся решению олимпиадных задач по математике с помощью теории графов. Ниже приведем описание предлагаемой нами этапной модели обучения учащихся решению олимпиадных задач по математике с помощью теории графов.

Первый этап – мотивационный – этап с проблемной задачей. Его цель – сформировать устойчивый интерес к решению олимпиадных задач по математике. Приведем примеры задач, которые будем использовать на данном этапе.

Задача 1 . Ваня решил поехать к бабушке из Астрахани в Тамбов. И может проехать через Волгоград и Саратов. Определите кратчайший путь из Астрахани в Тамбов.

	A	В	C	Т
A		4	3	11
B	4		2	1
C	3	2		6
Т	11	1	6

Выпишем пути и вычислим расстояния между пунктами.

ABCТ = 4 + 2 + 6 = 12; ACBТ = 3 + 2 + 1 = 6; ACТ = 3 + 6 = 9; ABТ = 4 + 1 = 5; AТ = 11.

Ответ: 5.

Задача 2 . Определите кратчайший путь из пункта А в пункт D.

При увеличении количества пунктов резко возрастает количество возможных путей. Использование перебора вариантов неэффективно, и необходим новый способ решения данного вида задач.

		A	B	C	D
A	A		2	4
B	B	2		1
C	C	4	1		5
D	D			5
E	E	6		1	3

Второй этап – ориентировочный – этап работы с типовыми задачами данной темы: задачи на нахождение количества путей и расстояния между пунктами, турниры (встречи), знакомства, логические («на рассуждение»). Его цель состоит в том, чтобы сформировать ориентировочную основу действий в решении задач по теории графов.

Ниже приведены требования к результатам обучения решению олимпиадных задач с помощью теории графов (см. табл. на с. 22).

Приведем примеры задач каждого типа.

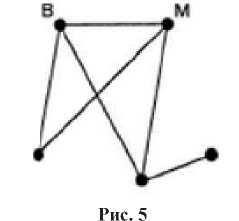
Задача 3 (нахождение количества путей). Определите количество путей из пункта А в пункт М.

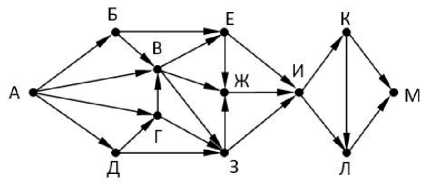
Рис. 2

Решение:

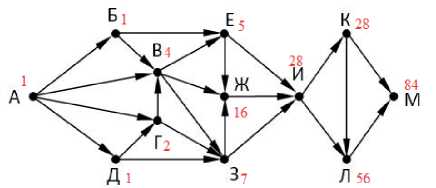
Рис. 3

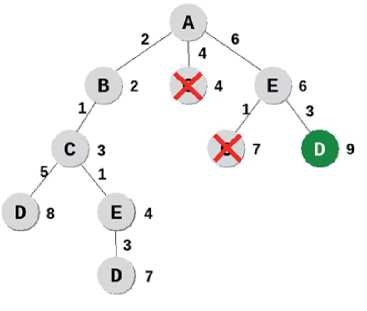
Рис. 1

Задача 4 (нахождение расстояния между пунктами). Определите длину кратчайшего пути между пунктами A и E.

	A	B	C	D	E
A		1
B	1		2	2	7
C		2			3
D		2			4
E		7	3	4

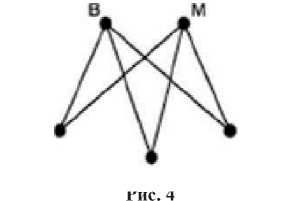
Задача 5 (турниры). В шахматном турнире по круговой системе, в котором участвуют 5 школьников, сыграно 6 партий. Больше всех встреч провели Ваня и Миша – по 3. Какое число партий сыграл участник, проведший наименьшее число встреч?

Решение. Рассмотрим два случая:

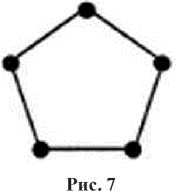
Задача 6 (знакомства). В компании, состоящей из пяти человек, среди любых трех человек найдутся двое знакомых и двое незнакомых друг с другом. Докажите, что компанию можно рассадить за круглым столом так, чтобы по обе стороны от каждого человека сидели его знакомые.

Решение. Построим граф знакомств, в котором вершины будут изображать людей, а ребро будет соединять две вершины. Легко показать, что существует ровно один граф с пятью вершинами, степень каждой вершины которого равна двум. Этому графу соответствует расположение людей за столом.

Задача 7 (логическая). На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Мнения девочек о том, как места распределились между победителями, разошлись.

Даша: Андрей был первым, Володя – вторым.

Галя : Андрей был вторым, Борис – третьим.

Лена: Боря был четвертым, Сережа – вторым.

Ася, которая была судьей на этих соревнованиях, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление. Кто из мальчиков какое место занял?

Решение. Построим граф (рис. 8).

• 1)    Ваня и Миша не играли друг с другом;

• 2)    Ваня и Миша сыграли друг с другом.

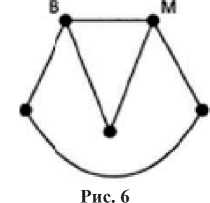
В первом случае каждый из остальных участников провел по 2 встречи (рис. 4).

Во втором случае возможны варианты:

• 2а ) существует участник, не встречавшийся ни с Ваней, ни с Мишей;

• 26)    каждый из участников встретился или с Ваней, или с Мишей (а может, и с каждым из них).

Изобразим все пять встреч, проведенных Ваней и Мишей.

2а. Этот случай невозможен, поскольку, проведя шестое ребро, мы получим противоречие с условием задачи, т. к. будет еще один участник, также сыгравший 3 партии (рис. 5).

• 2б.    Есть только одна возможность пронести шестое ребро, не нарушая условий задачи (рис. 6).

Поэтому наименьшее число встреч, проведенных участником, равно 2.

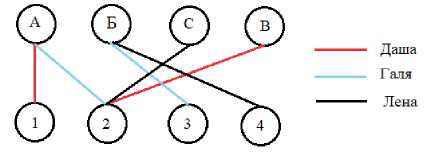
Рис. 8

Андрей – 1-е место, Сергей – 2-е место, Борис – 3-е место, Володя – 4-е место.

Третий этап – исполнительский – этап работы с задачами, аналогичными решенным. На данном этапе учащимся предлагаются задачи, в процессе решения которых необходимо воспроизвести ход действий в ситуациях,

ИЗВЕСТИЯ ВГПУ

Требования к результатам обучения решению олимпиадных задач с помощью теории графов

Метапредметные	Типы задач
Переводить практическую задачу в учебную	Нахождение количества путей Нахождение расстояния между пунктами Турниры (встречи) Знакомства Логические (на рассуждение)
Самостоятельно составлять алгоритм (или его часть), конструировать способ решения учебной задачи, оценивать его целесообразность и эффективность
Преобразовать одну форму представления информации в другую без потери смысла и полноты информации
Самостоятельно планировать деятельность (намечать цель, создавать алгоритм, отбирая целесообразные способы решения учебной задачи)
Владеть смысловым чтением текста задачи с целью решения различных учебных задач, для удовлетворения познавательных запросов и интересов – определять тему, главную идею задачи, цель; различать основную и дополнительную информацию, устанавливать логические связи и отношения, представленные в задаче; выявлять детали, важные для раскрытия основной идеи, содержания задачи	Турниры (встречи) Знакомства Логические (на рассуждение)
Распознавать ложные и истинные суждения, делать умозаключения по аналогии; приводить аргументы, подтверждающие собственное обобщение, вывод с учетом существующих точек зрения	Логические (на рассуждение)
Личностные	Типы задач
Осознавать потребность и готовность к самообразованию	Нахождение количества путей Нахождение расстояния между пунктами Турниры (встречи) Знакомства Логические (на рассуждение)
Использовать свои интересы для выбора индивидуальной образовательной траектории, потенциальной будущей профессии и соответствующего профильного образования
Предметные (знания и умения)	Типы задач
Знания о графе и его видах (классический, орграфы, деревья, эйлеров, полный и т. д.)	Нахождение количества путей Нахождение расстояния между пунктами Турниры (встречи) Знакомства Логические (на рассуждение)
Умения реализовывать некоторые алгоритмы на графах (алгоритм поиска в ширину, алгоритм двунаправленного поиска, метод накопления и т. д.)
Умение строить графовые модели условий текстовых задач

схожих с ранее рассмотренными. Его цель – закрепить полученные знания в обозначенной математической области.

Задача 8 (турниры). В соревновании по круговой системе с 12 участниками провели все встречи. Сколько встреч было сыграно?

Решение. Представим граф встреч, поскольку каждая пара встретилась между собой, то в графе каждая пара вершин будет соединена ребром. Мы должны найти число ребер в графе K₁₂. Из каждой вершины графа выходит 11 ребер. В произведении 11*12 каждое ребро учтено дважды, поэтому граф K₁₂ имеет (11*12)/2 = 66 ребер.

В общем виде можно вывести теорему о том, что граф Kn имеет n(n-1)/2 ребер.

Четвертый этап – преобразующий – этап решения задач, составленных варьированием условий опорных (типовых) задач. На данном этапе учащиеся должны самостоятельно осуществить выбор метода или сочетания методов при решении задач. Его цель – вооружить умением решать олимпиадные задачи с опорой на комбинаторику в условиях изменения задачной ситуации.

Задача 9 (турниры). В шахматном турнире, в котором каждый участник встречался с каждым, три шахматиста заболели и выбыли из турнира до того, как прошла его половина. Всего в турнире проведено 130 встреч. Сколько шахматистов участвовало в турнире?

Решение. Если в турнире участвовало 16 шахматистов, то число сыгранных ими партий не должно превосходить (16*15)/2 = 120. Поэтому в турнире играло больше 16 человек.

• А.    Если на начало турнира 17 участников, тогда 14 из них закончивших турнир провели между собой (14*13)/2 = 91 встречу, а выбывшие провели вместе 39, следовательно кто-то из них провел не менее 13 встреч, а значит, выбыл во второй половине турнира.

Б. Если на начало турнира 18 участников, тогда 15 из них закончивших турнир провели между собой (15*14)/2 = 105 встреч, а выбывшие провели вместе 25. Поскольку половина турниров составляет 8 туров, то выбывшие участники не могли провести более 24 встреч.

• В.    Если на начало турнира 19 участников, тогда 16 из них закончивших турнир провели между собой (16*15)/2 = 120 встреч, а выбывшие провели вместе 10. Каждый из них мог выбыть в первой половине турнира.

Г. Если на начало турнира 20 участников, тогда 17 из них закончивших турнир провели между собой (17*16)/2 = 136 встреч, т. е. больше, чем все участники турнира.

Следовательно, в турнире участвовало 19 человек.

Пятый этап – оценочный – этап самостоятельного решения олимпиадных задач (с опорой на теорию графов). Его цель – выяснить уровень готовности к участию в олимпиадах по математике различных уровней.

В качестве диагностической может быть предложена следующая работа.

Задача на нахождение количества путей (из коллекции задач Московской математической олимпиады).

В стране 15 городов, некоторые из них соединены авиалиниями, принадлежащими трем авиа- компаниям. Известно, что даже если любая из авиакомпаний прекратит полеты, можно будет добраться из любого города в любой другой (возможно, с пересадками), пользуясь рейсами оставшихся двух компаний. Какое наименьшее количество авиалиний может быть в стране?

Задача на нахождение расстояния между пунктами (из коллекции задач Московской математической олимпиады).

В некотором государстве города соединены дорогами. Длина любой дороги меньше 500 км, и из любого города в любой другой можно попасть, проехав по дорогам меньше 500 км. Когда одна дорога оказалась закрытой на ремонт, выяснилось, что из каждого города можно проехать по оставшимся дорогам в любой другой. Доказать, что при этом можно проехать меньше 1500 км.

Задача «Турниры» (из коллекции задач Московской математической олимпиады).

20 футбольных команд проводят первенство. В первый день все команды сыграли по одной игре. Во второй также все команды сыграли по одной игре. Докажите, что после второго дня можно указать такие 10 команд, что никакие две из них не играли друг с другом.

Задача «Знакомства» (из коллекции задач Московской математической олимпиады).

Каждый из 1994 депутатов парламента дал пощечину ровно одному своему коллеге. Докажите, что можно составить парламентскую комиссию из 665 человек, члены которой не выясняли отношений между собой указанным выше способом.

Задача на логику (из коллекции задач Турнира Ломоносова).

По кругу записаны 7 натуральных чисел. Известно, что в каждой паре соседних чисел одно делится на другое. Докажите, что найдется пара и несоседних чисел с таким же свойством.

В заключение отметим, что нами было выделено пять этапов обучения учащихся решению олимпиадных задач по математике (мотивационный, ориентировочный, исполнительский, преобразующий, оценочный) и выявлены требования к результатам обучения решению олимпиадных задач с помощью теории графов (метапредметные, личностные и предметные). На этой основе разработана система целесообразно подобранных задач в соответствии с каждым этапом обучения учащихся решению олимпиадных задач по математике с помощью теории графов. Данная система была апробирована в форме элективного курса «Приложение теории графов к решению олимпиадных задач» на базе МОУ «Гимназия 12

Краснооктябрьского района Волгограда» и показала свою эффективность. Успешное решение (три и более задач из пяти предложенных) диагностической работы большинством испытуемых позволяет рекомендовать предложенную систему задач как одно из важных средств обучения учащихся решению олимпиадных задач с помощью теории графов.