Оценивание значимости целей математического образования первокурсниками и абитуриентами

Анализ нормативных документов [14-16], научных публикаций [9-11, 13,18, 19] и материалов конференций [1, 2, 5] позволяет осознать необходимость изменений в системе образования и, как следствие, в процессе педагогического сопровождения образовательной деятельности. Внедрение компетентностного подхода в практику образования определило основные особенности его развития. Содержание образования как предметное поле формирования личности рассматривается сегодня как совокупность приобретаемых знаний, умений, навыков, ценностных установок, опыта деятельности и компетенции , необходимых для развития личности и эффективного включения её в жизнь общества [16].

Джон Биггс, автор Концепции конструктивного регулирования, представляющей собой структуру преподавания, базирующуюся на результатах, осознание конечных результатов обучения как компетенции представил следующей схемой (рис. 1) [3].

Таким образом, на сегодняшний день стратегическая задача образования - формирование действующих знаний, как новых качеств личности. Основными из них являются: самостоятельность, способность к мировоззренческому выбору и компетентному профессиональному действию, к самоуправлению, самообразованию и воспитанию.

Принцип гуманизации, являющийся одним из традиционных общепедагогических

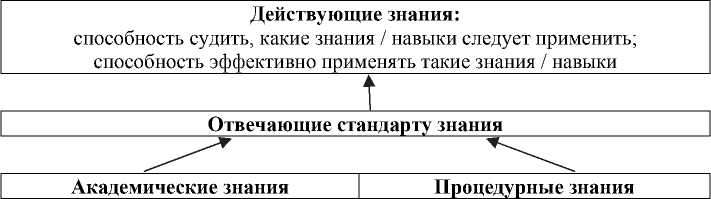
Рис. 1. Действующее знание (functioning knowledge) [3]

принципов, на современном этапе развития образования реализуется комплексностью традиционных и новых тенденций функционирования образовательной системы. Поэтому, разработка новых методов и интенсивных форм обучения в высшей школе остаётся актуальной.

В Федеральном Государственном Образовательном стандарте высшего профессионального образования (от 22 декабря 2009 г.) выделены два вида компетенций: общекультурные и профессиональные. Под общекультурными компетенциями (ОК) здесь понимается обобщённая группа компетенций, включающая разработанный в педагогике перечень ключевых образовательных компетенций.

В статье С. Берга [3] выражалось мнение о том, что очень сложно провести четкое различие между общекультурными компетенциями (универсальными) и предметно-специализированными компетенциями. Это было проиллюстрировано примером дескрипторов проекта «Тьюнинг». Так, способность решать задачи и способность применять знание на практике можно вполне назвать общекультурной компетенцией (ценностно-смысловой), в то время как способность решать числовые задачи, используя компьютерные и некомпьютерные методы, и способность решать задачи с помощью математических инструментов определяются как предметноспециализированные компетенции для естественных наук, к которым относится и математика. В своей статье С. Берг отметил, что, в этом нет никакого противоречия: «в определенной степени предметно-специализированные компетенции – это особый случай применения более широких, общекультурных компетенций к конкретной дисциплине, и они представляют собой совокупность методологий, образов мыслей и знания, специфических для этой дисциплины» [3, c. 186].

Математика всегда была неотъемлемой и существеннейшей составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научнотехнического прогресса и важной компонентой развития личности. Из спектра общекультурных компетенций, выделенных в государственном образовательном стандарте, при изучении математики явно развиваются следующие:

– способность владеть культурой мышления, способность к обобщению, анализу, вос- приятию информации, постановке цели и выбору путей ее достижения (ОК-1);

– способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ОК-10) [14, 15].

Вместе с тем следует заметить, что в учебном процессе неявно задействованы практически все общекультурные компетенции, перечисленные в ФГОС, так как все они имеют отношение к ключевым образовательным компетенциям. По мнению Ю.Г. Татура, обобщённый интегральный характер понятия компетенции и применение компетентностно-го подхода в государственных стандартах высшего образования третьего поколения обеспечит формирование обобщённой модели выпускника, абстрагированной от конкретных дисциплин и объектов труда, что позволит говорить о более широком поле его деятельности [12, c. 158].

Мы обратились к компонентному составу общекультурной компетенции выпускника вуза, в той части, которая обозначенаОК-10. Изучив ФГОС ВПО по направлениям подготовки 151900, 220400, 080200, мы отметили, что при изучении дисциплин математического и естественнонаучного цикла должна формироваться часть общекультурной компетенции (ОК-10), которая представляется как «способность использовать основные законы естественно-научных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования» [14, 15].

В рамках констатирующего эксперимента, мы ознакомились с диссертационными исследованиями [16], касающимися формирования компетенции, публикациями [9, 11, 13, 18], литературой [4, 7, 8, 10], что позволило нам определиться с проблемой.

Личностно-ориентированная парадигма образования ведёт к возрастанию роли социально-гуманитарных наук. Но на всех исторических этапах развития науки, ее уровень, в значительной степени, определялся математизацией различных отраслей знания. В связи с этим, высшее образование невозможно представить без математического образования, которое составляет основу научного знания. Однако специфика математики такова, что ее связь с обществом, в отличие от многих дру- гих наук, достаточно опосредована, поэтому изменения в математическом образовании, особенно в высшей школе, объективное требование времени. М.Д. Боярский на всероссийской конференции «Математика и общество» отметил, что одним из важных, основополагающих принципов реформирования математического образования в вузах должен стать принцип гуманитаризации, который выражается в приоритетном развитии общекультурных компонентов в содержании образования. При этом гуманитаризация математического образования понимается как часть единого процесса гуманитаризации естественно-научного образования и всей системы образования в целом. Необходимым условием, предпосылкой гуманитаризации высшего математического образования следует признать разработку его теоретических (методологических, педагогических и иных) основ. Эти основы должны обязательно включать в себя разработку целей высшего математического образования, его содержания, дидактических методов и средств, а также реализующих технологий [5]. Именно поэтому поиск новых эффективных средств в обучении математике не теряет своей актуальности.

Необходимость формирования общекультурных компетенций предопределяет культурологический подход . Семантическим ядром терминосистемы является понятие «культура», которое этимологически восходит к латинскому термину «culture» (возделывание, обрабатывание). Существует множество определений; достаточно краткое и ёмкое определение могло бы звучать так: культура – это технология (способ созидательной деятельности) общественного человека, это надприродный способ накопления и передачи человеческого родового и индивидуального опыта, его оценивания и осмысления, это то, что выделяет человека из внешнего мира и открывает путь самобытного свободного развития. Культура включает в себя и деятельность, и её результаты, смыслы и оценки [12, c. 169].

Представляя образование как способ вхождения человека в целостное бытие культуры, постижение и осуществление индивидом родовых и видовых смыслов жизни, следует отметить существующее несоответствие структуры и содержания образования структурам современной культуры и человеческой деятельности. Система педагогических методов и приёмов, направленных на развитие математических способностей студентов, долж- на иметь конечной целью формирование у него математической культуры. Математику следует рассматривать не только как один из рычагов научно-технического прогресса, но и как средство духовного роста. По словам Г. Вейля: «…Математика играет весьма существенную роль в формировании нашего духовного облика, занятие математикой – подобно миротворчеству, литературе или музыке – это одна из наиболее присущих человеку областей его творческой деятельности, в которой проявляется его человеческая сущность, стремление к интеллектуальной сфере жизни, являющейся одним из проявлений мировой гармонии» [17, c. 20].

Культурологический подход к конструированию содержания образования исследовался в работах С.И. Гессена, М.С. Кагана, Э. Кассирера, В.А. Конева, В.С. Степина, Е.Н. Шеянова и др. Мы в своём исследовании придерживаемся мнения Е.В. Бондаревской, которая определяет культурологический подход как «видение образования сквозь призму понятия культуры, то есть его понимание как культурного процесса, осуществляющегося в культуросообразной образовательной среде, все компоненты которой наполнены человеческими смыслами и служат человеку, свободно проявляющему свою индивидуальность, способному к культурному саморазвитию и самоопределению в мире культурных ценностей» [4, с. 44]. В результате такого подхода должно происходить формирование целостной культурной личности – «чтобы в человеке нашли отражение и природные, и социальные свойства, и его свойства как субъекта культуры, при этом развитие и природных и социальных начал представлено в контексте культурных свойств, имеющих общечеловеческую ценность» [8, с. 72].

Процесс образования в высшем учебном заведении должен быть направлен на обеспечение социально-профессионального становления личности, т. е. на удовлетворение потребности личности в социальном и профессиональном самоопределении. Осуществление образовательной деятельности может способствовать и усвоению знаний, и зарождению, а затем – становлению готовности будущих выпускников университета к исполнению профессиональных компетенций [11]. Целостная личность может быть развита только в целостном педагогическом процессе. Целостность требует единого концептуального подхода, объединяющего различные его компоненты (общая стратегия, цели, содержание, методы и формы, виды взаимодействия участников, методика оценивания результатов и т. д.), подчиненного общей идее подготовки специалиста, обладающего определенной системой профессиональноличностных качеств [13]. В содержательном плане целостность обеспечивается отражением в цели и содержании образования всего культурного опыта, накопленного человечеством, в организационном единстве компонентов, отражающих предметные, педагогические и личностные уровни взаимоотношения субъектов образовательного процесса. Вместе с тем, целостность проявляется не только в содержании и формах, но и в способах его усвоения, предполагающих раскрытие смыслового аспекта знаний через систему личностных структур сознания. В частности выпускники инженерных направлений должны осознавать, что успех в технической сфере требует широкой математической подготовки, поскольку только такая подготовка может обеспечить приспособляемость к непрерывно меняющимся типам задач, предъявляемых к решению. Осознание этого достигается в результате взаимодействия с педагогами, сопровождающими образовательную деятельность. В процессе педагогического сопровождения происходит взаимодействие с личностью, для того чтобы это взаимодействие привело к запроектированному результату необходимо обратиться к понятию личности. Понятие личности включает в себя совокупность присущих индивиду социальных качеств, которые образовались у него на основе природных свойств, в процессе активных взаимодействий с социальной средой и деятельности. Важнейшим регулятором деятельности является самосознание. Личность является одновременно и субъектом и объектом научнотехнического и общественного прогресса. Цель и смысл жизни человека должны быть связаны с развитием и реализацией его социальных сил в интересах как самой личности, так и всего общества. Развитие личности студентов вуза происходит путём качественных изменений, ведущих к новому уровню её целостности, а также становлением направленности. Направленность личности является результатом противоречивого единства социализации, т. е. усвоения социального опыта и культуры, и индивидуализации. Индивидуализация представляет собой сугубо индивидуальный способ и форму присвоения различ- ных отношений современного общества, обретение и развитие личностью своего «я» индивидуальных сущностных сил. Активность личности, как и деятельность, имеет избирательный характер. Развитие личности происходит под воздействием не любых, не всяких влияний, а главным образом тех из них, которые выражают потребности самого человека, включены в систему его личных ценностей, обращены к его личности, опираются на его собственное отношение к действительности.

Каждому человеку присуща индивидуальная, специфическая иерархия личностных ценностей, для которых характерна высокая осознанность. Они отражаются в сознании в виде ценностных ориентаций и служат важным фактором регуляции поведения. Ценностные ориентации - это особые, фиксированные качества личности, позволяющие ей ранжировать объекты по их значимости для неё. В своей совокупности они проявляются как интегративный внутренний фактор мотивации поведения и деятельности человека. От мотивации зависит, как и в каком направлении будут использованы различные функциональные способности, различные виды восприятия и мышления, интенсивность и упорство в осуществлении выбранного действия и достижение результатов. Мотивация очень часто ведёт к целеобразованию.

Опираясь на аксиологическое основание культурологического подхода, мы попытались хотя бы приблизительно обозначить место математики в системе личных ценностей сегодняшних выпускников школ г. Кыштыма и студентов младших курсов филиала ЮУрГУ в г. Кыштыме. Для чего обратились к анкете, разработанной В.М. Тихомировым. По мнению В.М. Тихомирова, обсуждению целей математического образования для личности естественно придать форму такого вопроса, который может быть адресован к любому взрослому человеку: «Если юноша или девушка, размышляющие о своём будущем, спросят Вас о том, что может им дать математическое образование? Зачем людей учат математике? Что Вы ответите?» [5, с. 4]. Такой вопрос задавался в разных аудиториях, большому числу респондентов (математиков и педагогов), ответы варьировались, но в конечном итоге группировались вокруг некоторых тем, которые впоследствии и были приведены в анкете. Анкетирование проводилось в США, Канаде, некоторых странах Европы, а также в России и странах бывшего Советского Союза.

Имеются обобщённые данные о распределении целей. Целью анкетирования в нашем случае, являлась попытка определения того насколько понимание целей математического образования опрошенными совпадает с целями, поставленными педагогическим сообществом. Учитывая состав опрошенных, людей с высокой математической культурой, мы считаем, что анализ расстановки целей поможет первоначально судить о понимании роли и места математического образования в системе ценностей. Андрей Николаевич Колмогоров говорил о трёх основных целях математического образования. Это признанный авторитет и его мнение, мы рассматривали как центр, а затем определяли порядок отклонения от центра. Расположение целей математического образования, по Колмогорову: 1) ориентация в окружающем мире; 2) подготовка к будущей профессии; 3) формирование мировоззрения.

Цели математического образования, как их видит математическое сообщество (на основе анализа опросов). Примерно так представляют себе цели математического образования учителя, педагоги, деятели просвещения: 1) интеллектуальное развитие; 2) ориентация в окружающем мире; 3) формирование мировоззрения; 4) физкультура мозга; 5) подготовка к будущей профессии; 6) подготовка в вуз [5, c. 4].

После обработки результатов опроса учеников 11 классов школ мы получили следующее распределение, приведённое в табл. 1.

Результаты опроса студентов 1-го курса отмеченных специальностей представлены в табл. 2.

Анализ полученных результатов, позволил нам сделать следующие выводы относительно видения целей математического образования студентами и потенциальными абитуриентами.

Сопоставление результатов (вертикальная шкала соответствует месту, на которое ставится соответствующая цель) приведено на гистограмме, которая иллюстрирует совпадение или рассогласование иерархии целей (рис. 2).

Во-первых, отметим тот факт, что ориентация в окружающем мире как цель располагается в конце ряда, хотя является одной из самых значимых. Все мы взаимодействуем с окружающим миром и всё, что связано с этим взаимодействием, что помогает нам в этом взаимодействии, является для нас ценным. Скорее всего, это объясняется тем, что между конструктивной математикой и математикой формальной, в том виде, в котором она преподаётся в настоящее время, существует непреодолимая для многих пропасть. Символы, которыми мы оперируем в математике, студентами воспринимаются, как существующие совершенно обособлено от пространственновременных форм, задачи – искусственными, не имеющими ничего общего с реальностью, что не способствует осознанию ценности математики в обычной жизни. Как следствие, возникает вопрос: «Зачем мне всё это нужно?». Изменению такой ситуации, по нашему мнению, может послужить разделение преподавания математики на две части:

• 1)    поисковая математика (конструктивная) – обращённая на объект ;

Таблица 1

Распределение целей математического образования (по мнению школьников)

Цель	1	2	3	4	5	6
Подготовка в вуз, %	39,62	16,98	18,87	13,21	5,66	5,66
Подготовка к будущей профессии, %	15,09	30,19	20,75	16,98	9,43	7,55
Интеллектуальное развитие, %	32,08	18,87	35,85	9,43	3,77	0,00
Формирование мировоззрения, %	1,89	9,43	1,89	7,55	43,40	35,85
Ориентация в окружающем мире, %	3,77	3,77	9,43	13,21	30,19	39,62
Физкультура мозга, %	7,55	20,75	13,21	39,62	7,55	11,32

Таблица 2

Распределение целей математического образования (по мнению студентов)

Цель	1	2	3	4	5	6
Подготовка в вуз, %	13,64	13,64	13,64	13,64	4,55	40,91
Подготовка к будущей профессии, %	4,55	27,27	31,82	18,18	13,64	4,55
Интеллектуальное развитие, %	59,09	13,64	13,64	9,09	4,55	0,00
Формирование мировоззрения, %	0,00	18,18	9,09	18,18	27,27	27,27
Ориентация в окружающем мире, %	0,00	4,55	13,64	27,27	31,82	22,73
Физкультура мозга, %	22,73	22,73	18,18	13,64	18,18	4,55

L

IlL.iiJh

• ■    Математическое сообщество

■ Школьники

1 О

• ■    По Колмогорову

• ■    Студенты

Рис. 2. Сравнение приписанных мест по категориям

• 2)    доказательная или образовательная математика – направленная на субъект и связанная с логикой. Математика должна восприниматься как нечто большее, чем совокупность специальных символов и терминов некоего условного языка. Точная терминология нужна для однозначного взаимопонимания в среде учёных, но коммуникационная функция должна быть отделена от познавательной, несмотря на взаимосвязь и взаимозависимость. Студенты должны осознать, что с помощью математических символов можно представлять и моделировать действительность, то есть окружающий мир. Именно в этом должна состоять основная цель преподавателя.

Во-вторых, тот факт, что и выпускники школ, и студенты первокурсники видят целью математического образования подготовку к будущей профессии и ставят её на второе и третье место указывает на то, что математическое образование по отношению к будущей профессии для них ценно. Абсолютное большинство опрошенных, не отрицает того, что математические знания и навыки необходимы практически во всех профессиях. Прежде всего, конечно, в тех, которые связаны с естественными науками, техникой и экономикой. Но в настоящее время несомненна необходимость применения математических знаний и математического мышления врачу, биологу, психологу, менеджеру и др. Потенциальные абитуриенты подтвердили это своими ответами.

Такое положение позволяет надеяться, что применение элементов контекстного обучения в рамках соответствующей специальности даст положительные результаты и позволит повысить уровень математического образования, а значит и общекультурный уровень обучающихся. Задача преподавателя заключается в установлении межпредметных связей, подборе комплексных задач, моделировании ситуаций в которых отрабатывались бы необходимые знания и навыки, а также способность к самостоятельному выбору и обоснованию выбора средств решения поставленных задач, способность к продуктивному диалогу.

В-третьих, то, что интеллектуальное развитие поставлено студентами первого курса на первое место, а для абитуриентов оно лишь на третьем, на наш взгляд объясняется наличием внешнего возмущающего фактора у школьников – необходимость выбора дальнейшего жизненного пути. Тот факт, что на первое место они ставят подготовку в вуз, доказывает ценность высшего образования, которое ведёт к интеллектуальному развитию . Математическое образование на данном этапе они воспринимают как средство достижения цели. Таким образом, через математику происходит стремление к интеллектуальному развитию. После достижения ближайшей цели – поступления в вуз, её ценность падает до 6-го места и на первый план выступает именно интеллектуальное развитие .

Основываясь на этом, убеждаемся, что одной из важнейших задач преподавателя математики является воспитание в человеке спо- собности понимать смысл поставленной перед ним задачи, умения правильно, логично рассуждать, прививать навыки алгоритмического мышления. Научить анализировать, отличать гипотезу от факта, критиковать, схематизировать, отчётливо выражать свои мысли и т. п. С другой стороны - развивать воображение и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения и т. д.). Иначе говоря, способствовать интеллектуальному развитию личности. Студенты и потенциальные абитуриенты рассматривают это как ценность и готовы к взаимодействию.

Физкультура мозга как цель математического образования вышла на первый план у студентов, в то время как для школьников она занимает только четвёртое место, что совпадает с мнением математического сообщества. Это можно объяснить тем, что изощрение ума -безусловная цель математического образования любого уровня. В частности, того образования, которое осуществляется в гуманитарных и технических вузах, не говоря уже об университетах. Тренировка ума так же необходима для полноценной жизни человека, как физкультура для тренировки тела. Мозг тренируют и занятия с компьютерами, и изучение языков, но лучше всего для этого приспособлена именно математика.

Что касается ценности математического образования для формирования мировоззрения. Философское постижение Мира, общих закономерностей и основных научных концепций также невозможно без математики. И потому, математика необходима для формирования мировоззрения. Но, для того чтобы обучающиеся поняли это, необходимо преподавать элементы истории математики и концепции современного естествознания. Знакомство с деятельностью ведущих учёных, основными направлениями научных исследований и др. в рамках существующих учебных планов возможно только в самостоятельной работе (рефераты, сообщения, наглядные пособия и др.) осуществляемой при содействии преподавателя (подбор тематики, постановка вопроса, идеи и др.). Кроме того в силу неопытности, респонденты могут не видеть грани между формированием мировоззрения и интеллектуальным развитием, именно поэтому отводят этой цели последние места.

В целом анализ анкет показал, на что нужно ориентироваться в плане мотивации студентов к изучению математики. Позволил взглянуть на математическое образование глазами аудитории, выявил недостатки, помог наметить пути их устранения.