Оценка гранулометрического состава кристаллов лактозы в сгущенном молочном продукте с сахаром и патокой крахмальной кислотной

Автор: Виноградова Юлия Владимировна, Гнездилова Анна Ивановна, Виноградова Людмила Алексеевна

Журнал: Молочнохозяйственный вестник @vestnik-molochnoe

Статья в выпуске: 4 (16), 2014 года.

Бесплатный доступ

Были выработаны образцы сгущенного молочного продукта с сахаром с частичной заменой сахарозы на патоку крахмальную кислотную, выполнена оценка гранулометрического состава кристаллов лактозы в продукте.

Патока, сгущенный молочный продукт, лактоза, гранулометрический состав, нормальный закон распределений

Короткий адрес: https://sciup.org/14998765

IDR: 14998765

Текст научной статьи Оценка гранулометрического состава кристаллов лактозы в сгущенном молочном продукте с сахаром и патокой крахмальной кислотной

В настоящее время в связи с активным развитием новых направлений производства сгущенных молочных продуктов, в которых в качестве сырья используют всевозможные заменители сахара, нередко стало наблюдаться ухудшение консистенции, вызванное неуправляемым ростом кристаллов лактозы и сахарозы. Как выяснилось [1], рост кристаллов в этом случае зависит не только от состава, но и от количества используемых ингредиентов молочного и немолочного происхождения.

Кристаллизация лактозы при охлаждении сгущенного молока с сахаром и других сгущенных молочных консервов является одним из основных технологических процессов в их производстве. Неуправляемая кристаллизация ведет к образованию крупных, органолептически ощущаемых кристаллов лактозы, что придает продукту мучнистую или даже песчанистую консистенцию [2].

Для оценки гранулометрического состава был выработан молочный продукт с сахаром с частичной заменой сахарозы на патоку крахмальную кислотную и отобраны его образцы.

В качестве основных характеристик гранулометрического состава приняты основные числовые статистические характеристики: распределение размера кристаллов лактозы по фракциям, средний размер кристаллов, среднеквадратическое отклонение. Средний размер и среднеквадратическое отклонение относятся к характеристикам положения распределения кристаллов лактозы по числовой шкале. Средний размер показывает положение центра распределения по числовой шкале [3, 4]. Среднеквадратическое отклонение указывает на величину усредненного отклонения кристаллов различного размера от центра распределения [5, 6]. Результаты представлены в таблице 1.

Таблица 1. Основные характеристики

Показатель	Срок хранения
Показатель	2 дня	6 мес	13 мес
Минимальный размер кристалла, мкм	1,2±0,05	1,5±0,07	1,6±0,02
Максимальный размер кристалла, мкм	6,5±0,02	8,2±0,05	8,5±0,05
Средний размер кристаллов лактозы, мкм	4,25±0,05	4,95±0,05	5,4±0,04
Среднеквадратическое отклонение	1,4±0,08	1,5±0,01	1,2±0,05
Коэффициент однородности	0,82±0,06	0,80±0,03	0,75±0,05

Величина коэффициента однородности определялась по кривым интегрального распределения (рис. 2). Численное значение коэффициента однородности соответствует отношению размера кристалла с вероятностью реализации 50 %, к размеру кристалла с вероятностью реализации 86 %. Коэффициент качества представляет собой величину коэффициента однородности, отнесенную к среднему размеру кристаллов.

В большинстве случаев для физических величин выполняется закон нормального распределения (закон Гаусса), плотность которого учитывает характеристики положения.

( x x1 )2

f(x) e ² ^σ

σ 2π где х – размер текущего кристалла, мм;

х1 – средний размер кристалла, мм;

о - среднеквадратическое отклонение размера кристалла от среднего размера.

Общий вид полигона распределения размера кристаллов по числовой шкале и вид дифференциальной кривой вероятностей для способа двухступенчатого охлаждения представлен на рисунке 1. Вид интегральной кривой вероятностей представлен на рисунке 2.

Соответствие фактического закона распределения конкретной физической величины теоретическому оценивается критерием согласия Пирсона [7].

k z2 = Ё (ni-npO2 •(n Pi)

i1 , где ni – фактическое число кристаллов, попадающих в данный интервал распределения по размеру, n – общее число замеренных кристаллов в выборке, pi – теоретическая плотность вероятности попадания кристаллов по размеру в данный интервал, соответствующий функции f(x).

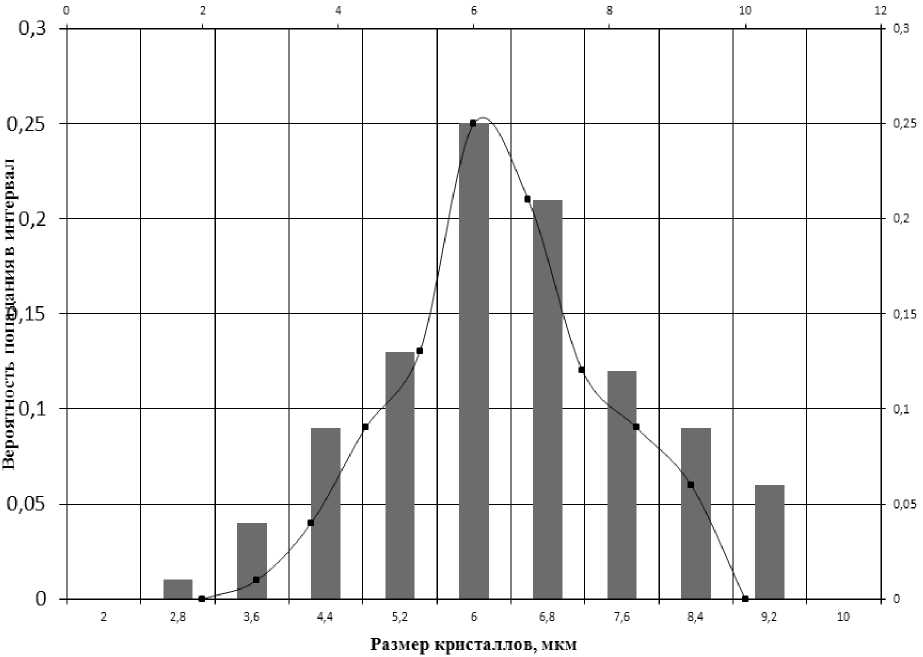
Рисунок 1. Полигон и дифференциальная кривая распределения

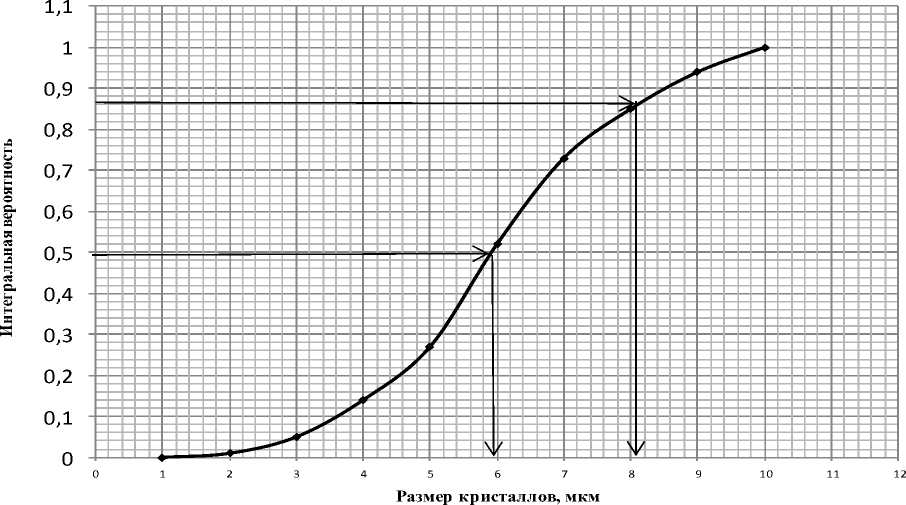
Рисунок 2. Интегральная кривая вероятностей

Доверительный интервал для технических приложений, которые оценивает диапазон возможных значений размера кристаллов определяется из условия:

x x₁ ± 3 σ

Пример определения вероятности попадания в интервал и коэффициента согласия Пирсона приведен в таблицах 2 и 3.

Таблица 2. Расчет доверительного интервала

Середина интервала	Экспериментальные вероятности	Нормальный закон
1,6	0	0,002002845
2,4	0,01	0,010331679
3,2	0,04	0,038379925
4	0,09	0,102670835
4,8	0,13	0,197787946
5,6	0,25	0,274386221
6,4	0,21	0,274116089
7,2	0,12	0,197204358
8	0,09	0,102166436
8,8	0,06	0,038116211
9,6	0	0,010240495
Сумма	1.0000	1.0000
Доверительный интервал при вероятности попадания в интервал 99,5 % -( 1,81=

Таблица 3. Проверка гипотезы нормального распределения

Диапазон	Экспериментальная частота	Интегральная вероятность попадания на границу интервала	Вероятность попадания в интервал	Теоретическая частота	Отклонение экспериментальной частоты от теоре тической
2	0	0,002096474	0,002096474	0,20964741	0,20964741
2,8	1	0,011002801	0,008906327	0,890632711	0,013430007
3,6	4	0,042964594	0,031961793	3,196179328	0,202156264
4,4	9	0,126254579	0,083289985	8,328998451	0,054057289
5,2	13	0,283905421	0,157650842	15,7650842	0,484976201
6	25	0,500685778	0,216780357	21,67803575	0,509061182
6,8	21	0,717258487	0,216572709	21,65727089	0,019947343
7,6	12	0,87445669	0,157198202	15,71982022	0,880230327
8,4	9	0,957348416	0,082891726	8,289172602	0,060956095
9,2	6	0,989096395	0,031747979	3,17479789	2,514102391
10	0	0,997926164	0,008829769	0,882976935	0,882976935

Результаты оценки соответствия эмпирического распределения нормальному закону на основе расчетов коэффициента согласия Пирсона приведены в таблице 4 и на рисунке 3.

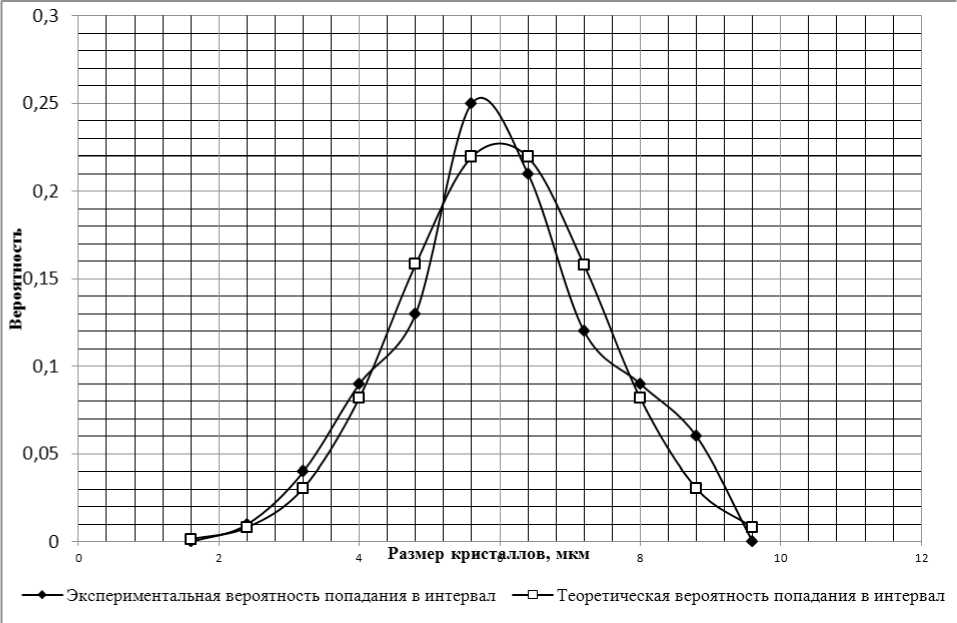
Рисунок 3. Эмпирические вероятности и нормальный закон Распределения

Таблица 4. Результаты оценки согласия эмпирических данных нормальному закону распределения

Показатели	Величина показателя при сроке хранения
Показатели	2 суток	6 мес.	13 мес.
Доверительный интервал, мкм	0,98-8,20	1,31-10,07	1,81-10,18
Коэффициент Пирсона	5,30<5,35	6,32<7,20	5,83<6,35

Из анализа результатов таблиц следует, что полученный обобщенный коэффициент согласия Пирсона меньше табличного значения этого коэффициента, соответствующего вероятности реализации, принятой в зависимости от количества интервалов разбивки (степеней свободы). Это подтверждает, что оцениваемые выборки по характеру распределения близки к теоретическому нормальному распределению с полученными характеристиками положения, х1 и σ.

Список литературы Оценка гранулометрического состава кристаллов лактозы в сгущенном молочном продукте с сахаром и патокой крахмальной кислотной

Гнездилова, А. И. Консервированный молочный продукт с сахаром и крахмальной патокой/А. И. Гнездилова, Л. А. Куренкова//Молочная промышленность. -2013. -№9. -С. 84-85.
Чекулаева, Л. В. Сгущенные молочные консервы/Л. В. Чекулаева, Н. М. Чекулаев. -М.: Легкая и пищевая пром-сть, 1982. -263 с.
Смирнов, Н. В. Курс теории вероятностей и математической статистики для технических приложений/Н. В. Смирнов, И. В. Дунин-Барковский. -М.: Наука, 1969. -512 с.
Корн, Г. Справочник по математике для научных работников и инженеров. Определения, теоремы, формулы/Г. Корн, Т. Корн. -М.: Наука, 1973. -832 с.
Абчук, В. А. Справочник по исследованию операций/Под ред. Ф. А. Матвейчука. -М.: Воениздат, 1979. -368 с.
Коузов, П. А. Основы анализа дисперсного состава промышленных пылей и измельченных материалов/П. А. Коузов.-Л.: Химия, 1987. -264 с.
Вентцель, Е. С. Теория вероятности и ее инженерные приложения: учебное пособие для втузов/Е. С. Вентцель, Л. А. Овчаров. -М.: Высшая школа, 2000 -480 с.

Статья научная