Оценка опережающего индикатора ВРП методом темпорального дезагрегирования

Понимание основных макроэкономических трендов становится особенно важным в условиях высокой экономической неопределенности. Для анализа текущей и будущей экономической динамики в развитых странах распространена практика использования опережающих индикаторов, которые имеют идентичную динамику с валовым внутренним продуктом (ВВП), но при этом характеризуются более высокой частотой [1]. На региональном уровне двухлетнее запаздывание публикаций официальных статистических данных годовых значений валового регионального продукта (ВРП), а также отсутствие квартальных и ежемесячных данных о его динамике являются препятствием для раннего формирования представления об изменении общей тенденции региональной экономики и проведения качественного анализа текущей ситуации. В то же время наличие оперативной статистической экономической информации из официальных и альтернативных источников, а также эконометрических инструментов мотивируют на разработку опережающего индикатора, характеризующегося высокой частотой (ежемесячной или квартальной), согласованностью с динамикой оперативных экономических данных и при этом обеспечивающего высокое качество прогнозирования годовой динамики ВРП.

Одним из математических подходов к получению высокочастотных данных из низкочастотных является частотное преобразование (frequency conversion). В случае работы с временными рядами типа потока такой процесс преобразования называется темпоральным (или временным) дезагрегированием (temporal disaggregation) (ТД). Задача ТД заключается в получении на основе известных высокочастотных (ежемесячных или квартальных) значений индикаторов таких оценок неизвестного (ненаблюдаемого) высокочастотного показателя, которые при агрегации сводятся к значениям низкочастотного (годового) показателя.

Методы ТД обычно используются для получения высокочастотных опережающих индикаторов на национальном уровне. В данной статье фокус сосредоточен на апробации методов временной дезагрегации на региональном уровне. Для этого в первой части работы представлена формализация задачи темпорального дезагрегирования ВРП, рассмотрены модификации методов и возможности их программной реализации. Далее приводятся результаты обзора эмпирических зарубежных и российских работ по темпоральному дезагрегированию ВВП и ВРП, которые способствовали выбору методов оценивания и первоначальному набору индикативных переменных. Продемонстрированы результаты оценки опережающего индикатора ВРП методом ТД и его прогноза с помощью ARIMA -модели на примере Республики Башкортостан. Выводы по результатам проведенного исследования сформулированы в заключении.

Методы темпорального дезагрегирования и их программная реализация

Впервые задача временного дезагрегирования была поставлена J. H. C. Lisman, J. Sandee [2] и F. T. Denton [3] с использованием методов квадратической оптимизации. Позже G. C. Chow и A. L. Lin [4] предложили метод темпорального дезагрегирования, основанный на регрессии, связывающей низкочастотный временной ряд с независимыми высокочастотными временными рядами. Этот метод хорошо зарекомендовал себя и нашел дальнейшее развитие в работах R. B. Fernandez [5] и R. B. Litterman [6], которые допускают сложные нестационарные структуры ошибок регрессии. Другие обобщения метода Чоу–Лина1 предполагают многомерное расширение [7], использование динамических линейных зависимостей в виде моделей авторегрессии проинтегрированного скользящего среднего (autoregressive integrated moving average, ARIMA) [8] и моделей пространства состояний [9; 10], приближение с использованием логарифмов [11] и др.

Проблему темпорального дезагрегирования лучше всего рассматривать с практической точки зрения. Пусть имеем наблюдаемый за T лет низкочастотный (годовой) ряд ВРП, который обозначим y i ( i = 1,…, T ). Нужно построить ненаблюдаемый временной ряд частоты M (месячной или квартальной): x t ( t = 1,…, MT ). Этот высокочастотный ряд и будет представлять собой опережающий индикатор ВРП. При этом дезагрегированный ряд x t должен соотноситься в течение каждого года с наблюдаемым рядом ВРП y i . В нашем случае это означает, что сумма значений полученного высокочастотного ряда внутри каждого года должна совпадать с соответствующим годовым значением ряда ВРП:

M yi = ∑ m=1

x ( i - 1 ) M + m .

Кроме того, при дезагрегации предполагается, что внутригодовая динамика ненаблюдаемого ежемесячного ряда должна быть согласована с динамикой индикаторных переменных с такой же частотой.

Таким образом, согласно подходу Чоу– Лина темпоральное дезагрегирование производится на основе следующей регрессии, связывающей значения искомого высокочастотного ряда со значениями одного или нескольких рядов высокочастотных индикаторов:

x_t = Z_t ×β+ a_t ,               (1)

где Zt – матрица k индикаторных высокочастотных переменных; β – вектор оцениваемых коэффициентов; at – случайная переменная с нулевым средним и ковариационной матрицей V; xt – ненаблюдаемый высокоча- стотный ряд, для которого сумма за год совпадает со значениями низкочастотного ряда yi.

Метод Чоу–Лина может применяться как с включением, так и без включения временных рядов индикаторных переменных Z t . Чтобы оценить регрессию (1), используется обобщенный метод наименьших квадратов, для реализации которого требуется задать значения ковариационной матрицы V , которые, в свою очередь, на практике неизвестны. G. C. Chow и A. L. Lin предположили, что ошибки следуют авторегрессионному процессу AR (1):

a_t = p × a_{t - 1} +ε _t , (2)

где ε t ∼ N (0, σ ²) 1 – гауссовский «белый шум», | ρ | < 1.

Модификации метода Чоу–Лина используют различные предположения о структуре ковариационной матрицы V . Подход Фернандеса предполагает, что остатки представляют собой случайное блуждание (т. е. ρ = 1 в предыдущей формуле): a t = a t –1 + ε t , где ε t ∼ N (0, σ ²).

Подход Фернандеса является частным случаем подхода Литтермана, согласно которому остатки описываются моделью ARIMA (1, 1, 0): a t = a t –1 + ε t , где ε t ∼ N (0, V ), ε t = ρ × ε t – 1 , | ρ | < 1.

Современные специализированные эконометрические пакеты позволяют автоматизировать процедуру ТД. В частности, в известных программных продуктах в области эконометрики, таких как RATS и EViews (разработчики – Estima и IHS Markit соответственно), реализованы методы Чоу–Лина, Лит-термана и Фернандеса. Помимо этого, программа ECOTRIM, разработанная Европейским статистическим бюро специально для целей ТД, обладает расширенным набором методов темпорального дезагрегирования по сравнению с RATS и EViews. Пакет прикладных программ MATLAB также содержит в своем составе функции для разных методов темпорального дезагрегирования. Наиболее полно методы ТД представлены в разработанном C. Sax и P. Steiner [12] пакетe tempdisagg языка программирования R, который отличается открытым программным кодом. В tempdisagg реализованы следующие стандартные методы ТД: Denton, Denton–Cholette, Chow–Lin, Fernandez, Litterman. С учетом полноты охвата методов для реализации темпорального дезагрегирования ряда ВРП выбрана среда RStudio для языка программирования R и пакет tempdisagg.

Обзор эмпирических исследований

Процедура ТД активно применяется в зарубежных исследованиях, которые различаются страновым охватом, периодом исследования, методом разложения и набором индикаторных переменных.

В качестве примеров эмпирических работ, реализующих методы ТД на данных развитых экономик, можно привести исследования [11; 13–18]. Так, авторами [13] проводится преобразование квартальной динамики ВВП в ежемесячную для стран группы G 7 за период 1985– 2000 гг., наиболее надежные результаты при этом обеспечивает метод Чоу–Лина. Разработанные авторами модели ТД для разных стран отличаются набором индикаторных переменных, в качестве которых используются показатели, характеризующие развитие промышленного производства, строительства, розничных продаж, а также индекс потребительских цен, процентная ставка, уровень безработицы, число вакансий, индекс доверия домашних хозяйств и фирм и пр. При этом индекс промышленного производства (или его близкий аналог для тех стран, в которых этот показатель недоступен) является единственной переменной, входящей в модель для каждой страны. Например, в случае Канады проведение темпорального дезагрегирования позволило авторам оценить расхождения между фактическими и расчетными данными, так как в стране ведется учет ежемесячных данных ВВП. Кроме того, показано, что комбинация методов ТД с динамическими моделями (в частности, с bridge -моделями) позволяет улучшить краткосрочный прогноз ВВП [13].

В работе [14] из-за недоступности квартальных национальных счетов Италии дезагрегация годовых значения ВВП за период 1990–2008 гг. осуществлялась на основе подходов Чоу–Лина и Фернандеса с включением в качестве индикаторной переменной индекса промышленного производства.

Результаты дезагрегации квартальных данных ВВП Германии с 1991 по 2008 г. представлены в работе [15]. Показано, что ежемесячная дезагрегированная динамика ВВП тесно коррелирует с динамикой индексов деловой активности, бизнес-климата и деловых ожиданий в течение ближайших шести месяцев, которые рассчитываются на основе опроса компаний немецким институтом IFO .

Развитию методов ТД в условиях, когда число индикаторов значительно выше размера низкочастотных данных, посвящена работа [16]. Предлагаемая авторами процедура разреженной дезагрегации апробирована на квартальных данных ВВП Великобритании в интервале 2008–2020 гг. В качестве индикаторов рассматривались 97 показателей с ежемесячной периодичностью, среди которых оборот производственных отраслей, оборот в сфере услуг, индекс розничных продаж, оборот отраслей на основе деклараций по НДС, объем транспортного потока на дорогах и в портах и др. Более ранние ежемесячные оценки логарифмов четырех компонент ВВП (сельское хозяйство, строительство, общественные и частные услуги) Великобритании – за 1976–2003 гг. – представлены в работе [11]. В качестве индикаторных переменных, которые использовались только для модели сектора частных услуг, рассматривались показатели розничной торговли и промышленности.

В работе [17] решается проблема одновременного получения с помощью моделей Чоу– Лина квартальных значений валовой добавленной стоимости для регионов Испании, согласующихся с годовыми региональными и квартальными национальными счетами.

Дезагрегация ВВП стран ЕС за 1995–2006 гг. осуществлена в исследовании [18] на основе обобщенных моделей Чоу–Лина и Фернандеса в виде модели пространства состояний с включением индикаторных переменных и тренда. Авторами получены ежемесячные значения валовой добавленной стоимости по секторам экономики, а также составляющих по расходам, которые затем агрегировались в ежемесячную оценку ВВП. В частности, модель для выпуска в промышленности включала индекс промышленного производства, численность занятых, количество отработанных часов и показатели бизнес-обследований (индекс промышленной уверенности, оценка уровня портфеля заказов, оценка динамики производства за последние месяцы).

Апробация методов ТД для развивающихся стран, которые зачастую характеризуются наличием официальных данных ВВП только с годовой периодичностью, проведена в работах [19–24]. Квартальные оценки реального ВВП с 1970-х гг. по 1993 г. в работе [19] рассчитаны методами Чоу–Лина для стран Восточной и Юго-Восточной Азии (Китай, Индонезия, Малайзия, Филиппины и Таиланд), при этом спецификации для разных стран отличаются. Для Малайзии ввиду наличия качественных статистических данных квартальные оценки ВВП получены как сумма дезагрегированных выпусков трех секторов экономики (промышленность, сельское хозяйство и сфера услуг). При этом в качестве индикаторов для отраслевых выпусков используются индекс промышленного производства, объем экспортной и импортной торговли, общий объем ссуд коммерческих банков. Для Китая, Индонезии и Таиланда дезагрегация годовых значений ВВП осуществляется с включением в регрессию объемов внешней торговли и денежного агрегата M1, индексов производства в горнодобывающей и обрабатывающей промышленности. Прогнозы ВВП в дальнейшем получены на основе ARIMA -модели. Разработанные квартальные оценки ВВП этих стран используются в дальнейшем макроэкономическом моделировании с применением векторной авторегрессии.

Дезагрегированная ежемесячная динамика ВВП Бразилии за 2003–2020 гг. оценена автором исследования [20] на основе динамической модели с помощью фильтра Кальмана с включением широкого набора оперативных переменных, среди которых уровень использования мощностей, объемы экспорта и импорта, потребления электроэнергии, оборот торговли, индексы производства отдельных видов промышленной продукции, индексы ожиданий и текущей ситуации на основе опроса потребителей. Показано, что качество прогноза квартального ВВП существенно повышается при включении в модель ТД лагов индикаторных переменных и индекса экономической активности Центрального Банка Бразилии ( IBC-Br ).

В работе [21] производится дезагрегирование квартальных данных ВВП Индонезии за 2000–2016 гг. с включением в качестве индикатора индекса производства в обрабатывающей промышленности. На основе дезагрегированной ежемесячной динамики ВВП исследованы внутригодовые пики экономической активности в стране и получен прогноз. В работе [22] также реализуется частотное разложение квартального ВВП Индонезии за 2000– 2018 гг. с учетом индекса производства. Прогноз высокочастотного индикатора ВВП строится с помощью ARIMA -модели.

В статье [23] выполнено разложение годовой динамики ВВП Нигерии в интервале 1981–2012 гг. Наилучшие результаты получены на основе метода Литтермана, наихудшие – на основе метода Дентона. В качестве индикаторных переменных рассматривались высокочастотные ряды импорта и экспорта, однако получить статистически значимые результаты авторам не удалось.

Дезагрегация годовых рядов ВВП в квартальные с помощью подхода Чоу–Лина для островных государств Южной части Тихого океана проведена авторами [24]. При этом объемы денежной массы (М1 и М2), экспорта, индекс цен и обменный курс рассматриваются в данной работе как предикторы.

Динамика российского ВВП дезагрегирована в работах [25–28]. Так, автор исследования [25] представляет иллюстративные расчеты разложения квартальной динамики ВВП Российской Федерации в 2011–2015 гг. методом Дентона с учетом месячной динамики индекса выпуска товаров и услуг по базовым видам экономической деятельности (ВЭД), обеспечивая условие сохранения формы ее сезонного цикла. Эта методика получила дальнейшее развитие в работе [26], где демонстрируется дезагрегация квартальных рядов составляющих элементов ВВП с обеспечением выхода на квартальные объемы с максимальной точностью, сохранением всех балансовых связей между рядами и гладкости в динамике дефляторов. Коллективом авторов работы [27] представлены результаты ТД годовых значений ВВП России на квартальные за период 2009–2018 гг. Наилучшие результаты отмечаются для спецификации, оцененной методом Литтермана и включающей в качестве индикаторов оценки опережающего индикатора ВВП на основе методологии Росстата, а также такие показатели мониторинга предприятий Банка России, как обеспеченность предприятий заказами, изменение спроса на продукцию (услуги). Полученная модель дезагрегации ВВП используется в дальнейшем для расчета квартальных значений суммарного ВРП по России и по федеральным округам.

Месячный индикатор ВВП России также оценен в работе [28] на винтажных данных на трех разных подвыборках. С точки зрения устойчивости оценок модели к пересмотру или появлению новых данных, авторы предпочли использовать модель Чоу–Лина и ее модификации, динамические модели ТД, а также их комбинирование (усреднение). Из-за большого числа факторов, среди которых рассматривались показатели выпуска, финансового сектора и показатели ожиданий на основе мони- торинга предприятий Банка России, модели оценивались с использованием метода главных компонент и фильтра Кальмана. Хорошими индикаторами для интерполяции оказались показатели выпуска по основным ВЭД.

Подводя итог проведенному обзору зарубежных и отечественных эмпирических исследований в области дезагрегации экономических временных рядов, можно отметить низкий уровень апробации этих методов на региональных данных. Методы ТД для разных стран позволяют получать надежные оценки высокочастотных индикаторов ВВП, при этом наибольшую значимость демонстрируют показатели промышленности и торговли. Кроме того, за счет включения в модель дезагрегации показателей опроса предпринимателей или потребителей качество прогнозных оценок ВВП, как правило, улучшается.

МАТЕРИАЛЫ И МЕТОДЫ

Исходными данными для исследования послужили показатели Росстата, а также данные мониторинга предприятий нефинансового сектора, проводимого Банком России 1 на регулярной основе. В качестве низкочастотного интерполируемого ряда рассматривался ВРП Республики Башкортостан на интервале 2009–2022 гг. в сопоставимых ценах базового 2009 г. (рис. 1). Значения ряда получены на основе официальных данных Росстата о ВРП (в текущих ценах, млрд руб.) и индексов физического объема валовой добавленной стоимости (в процентах к предыдущему году).

С учетом результатов анализа литературных источников отобраны следующие высокочастотные индикаторные переменные с января 2009 г. по апрель 2024 г.:

– ежемесячные индексы основных экономических показателей, публикуемых Росстатом 2

(индекс промышленного производства 1 – ИПП, оборот розничной торговли 2 – ОРТ), объем платных услуг населению, объем работ, выполненных по ВЭД «Строительство»;

– ежемесячные опросные данные мониторинга предприятий Банка России 3 (изменения экономической конъюнктуры, изменения экономического положения, индикатор биз-нес-климата, изменения валютного курса рубля и др.).

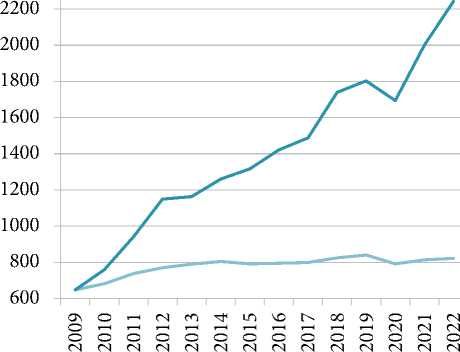
^^^^^^^^n В ценах 2009 г. ^^^^^^^^» В текущих ценах Источник : составлено автором.

Рис. 1. Динамика ВРП

Республики Башкортостан (в текущих и сопоставимых ценах 2009 г., млрд руб.)

Fig. 1. Dynamics of the gross regional product of the Republic of Bashkortostan (in current and comparable prices of 2009, billion rubles)

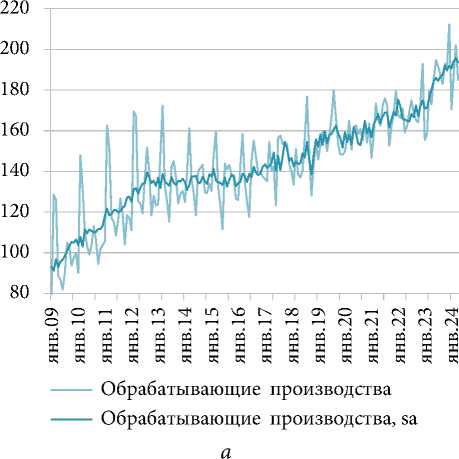
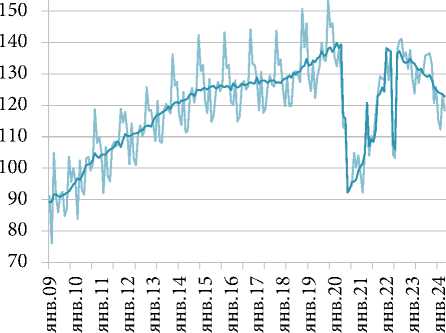
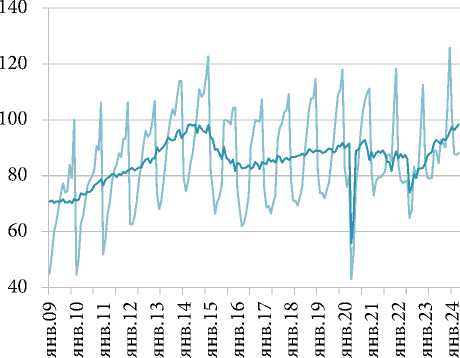
Динамика показателей с высокой статистической значимостью в модели ТД приведена на рис. 2.

Основу исследования составили методы сезонной корректировки X-13ARIMA-SEATS, методы и модели темпорального дезагрегирования, а также модели ARIMA. При этом задача ТД сводится к оценке ежемесячных значений опережающего индикатора, суммарные значения которого за год совпадают с соответствующими годовыми значениями ВРП. Для повышения точности аппроксимации годовых значений ВРП высокочастотными значениями опережающего индикатора производился отбор высокочастотных индикативных переменных. Последовательность шагов исследования можно обобщенно описать следующим образом. Перед анализом все высокочастотные временные ряды подверглись сезонной корректировке методом X-13ARIMA-SEATS (см. рис. 2). На первом шаге производилось построение моделей ТД годовой динамики ВРП с перебором индикаторных переменных и методов оценивания с последующим выбором лучшей спецификации и оценкой ежемесячных значений опережающего индикатора ВРП на ее основе. На следующем шаге осуществлялось моделирование и прогнозирование полученного на предыдущем шаге опережающего индикатора ВРП на основе модели ARIMA. На третьем шаге осуществлена процедура темпорального агрегирования для прогнозного значения опережающего индикатора ВРП и формирование таким образом прогноза ВРП. На последнем шаге осуществлен анализ вневыборочного прогноза ВРП.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Согласно описанной логике исследования дезагрегация годовых значений ВРП Республики Башкортостан проводилась с учетом ежемесячной динамики индикаторных переменных. Как и в случае регрессионных моделей, в моделях ТД при работе с короткими временными рядами имеются ограничения на число включаемых индикаторных переменных. По- этому осуществлялось многократное построение моделей ТД с разными наборами индикаторных переменных и отбор из них значимых. Согласно рекомендациям разработчиков библиотеки в R [12] первоначально в качестве метода ТД выбирался метод Чоу–Лина. На этом этапе набор индикаторных переменных существенно сузился.

Добыча полезных ископаемых

Добыча полезных ископаемых, sa b

ОРТ непродовольственными товарами

ОРТ непродовольственными товарами, sa

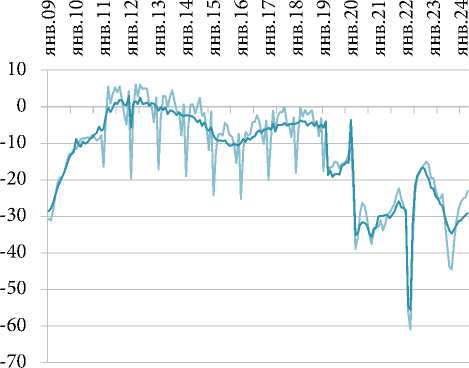
Влияние изменения валютного курса рубля

Влияние изменения валютного курса рубля, sa d

c

Источник : составлено автором.

Рис. 2. Динамика показателей (исходных и сезонно скорректированных, sa ) для моделирования: а – ИПП по ВЭД «Обрабатывающие производства», в % к декабрю 2009 г.;

b – ИПП по ВЭД «Добыча полезных ископаемых», в % к декабрю 2009 г.;

c – ОРТ непродовольственными товарами, в % к декабрю 2009 г.;

d – изменение валютного курса рубля, баланс ответов, в %

Fig. 2. Dynamics of indicators (initial and seasonally adjusted) for modeling:

а – FEA IPI “Manufacturing”, in % by December 2009;

b – FEA IPI “Resource Development”, in % by December 2009;

c – retail turnover for non-food goods, in % by December 2009;

d – fluctuations in ruble exchange rates, answers, in %

Далее процедура ТД продолжалась с включением отобранных индикаторных переменных на основе модификаций метода Чоу–Лина 1 , которые отличаются подходами к оценке авторегрессионного коэффициента в формуле (2).

Выбор лучшей спецификации модели ТД осуществлялся с учетом значимости факторов (на основе t- критерия), а также показателей качества подгонки (на основе скорректированного коэффициента детерминации, R _a ² _dj , информационных критериев Акаике – AIC и Шварца – BIC ) и качества прогноза (на основе средней абсолютной ошибки в процентах – MAPE ).

Результаты оценивания некоторых моделей методами ТД, содержащих разное число индикаторных переменных, показаны в табл. 1–2.

При этом индекс производства по промышленности (в целом или по ВЭД) является статистически значимой переменной в любой спецификации, независимо от метода оценивания и набора других переменных.

Как видно из табл. 1, спецификации 1–4 в качестве индикаторных переменных включают только показатели официальной статистики. Показатели строительства и розничной торговли оказались статистически незначимыми (модели 1–2) и из дальнейшего анализа были исключены. Добавление в анализ ИПП в разрезе отдельных ВЭД, индексов оборота розничной торговли по типам товаров, а также показателей мониторинга предприятий Банка России позволило улучшить качество моделей 5–7.

Табл. 1. Результаты темпорального дезагрегирования методом Чоу–Лина

Table 1. Results of temporal disaggregation by the Chow–Lin method

Индикаторная переменная	Модель (метод Chow-Lin-Maxlog )
	1	2	3	4	5	6	7
Свободный член	15,32 *	1,13	3,52	17,37 ***	21,23 ***	20,05 ***	19,16 ***
ИПП	0,25 ***	0,31 ***	0,28 ***	–	0,26 **	–	–
ИПП «Добыча полезных ископаемых»	–	–	–	0,13 ***	–	0,11 **	0,13 ***
ИПП «Обрабатывающие производства»	–	–	–	0,10 ***	–	0,14 ***	0,11 ***
ОРТ	0,09	0,10	–	–	–	–	–
ОРТ непродовольственными товарами	–	–	0,14	0,20 ***	0,14 *	0,16 **	0,18 **
Объем платных услуг населению	0,19 **	0,18 *	0,16 *	–	–	–	–
Объем работ по ВЭД «Строительство»	–0,12 **	–	–	–	–	–	–
Изменение валютного курса рубля	–	–	–	–	0,10 **	0,06 *	–
Изменение экономической конъюнктуры	–	–	–	–	–	–	0,06
AR -параметр	0,00	0,67	0,58	0,00	0,56	0,00	0,00
Показатели качества модели
2 R adj	0,98	0,95	0,96	0,98	0,97	0,99	0,98
MAPE , %	0,81e-16	1,17e-16 1,15e-16		1,38e-16	1,03e-16	0,85e-16	1,05e-16
AIC	1,85	0,66	0,78	1,93	0,66	1,58	1,75
BIC	2,08	0,84	0,97	2,11	0,85	1,81	1,98
Источник : рассчитано автором. Примечание : «-» - невключение в модель фактора, U*“ ^ ** - на 0,01 %-м, L * - на 0,05 %-м, Li- на 0,1 %-м.			– значимость коэффициентов на 0,001 %-				м уровне,

¹ Модификации метода Чоу–Лина отличаются альтернативными итерационными процедурами оценки параметра авторегрессии ρ в формуле (2). В классическом методе Чоу–Лина авторегрессионный параметр выводится из наблюдаемой автокорреляции низкочастотных остатков. Для получения оценки параметра авторегрессии методом Сhow-Lin-Maxlog максимизируют функцию правдоподобия регрессии, оцениваемой обобщенным методом наименьших квадратов. Подходы Chow-Lin-Minrss-Ecotrim и Chow-Lin-Minrss-Quilis минимизируют взвешенную сумму квадратов остатков, используя алгоритмы, предложенные и реализованные R. Barcellan в ECOTRIM и E. M. Quilis в MATLAB соответственно.

Табл. 2. Результаты темпорального дезагрегирования модифицированными методами Чоу–Лина и Литтермана

Table 2. Results of temporal disaggregation by modified

Chow–Lin and Litterman methods

Индикаторная переменная	Метод темпорального дезагрегирования в R
	Chow-Lin-Minrss-Ecotrim			Chow-Lin-Minrss-Quilis				Litterman-Minrss
	8	9	10	11	12	13	14	15	16
Свободный член	20,39 ***	7,06	13,47 **	16,96	18,61	18,99 *	28,36 *	42,64 ***	31,62 **
ИПП	–	0,26 ***	–	–	0,22 **	–	0,20 **	–	0,12
ИПП «Добыча полезных ископаемых»	0,10 **	–	0,14 ***	–	–	0,11 *	–	–	–
ИПП «Обрабатывающие производства»	0,11 ***	–	0,12 ***	0,18 **	–	0,10	–	–	–
ОРТ	–	–	0,24 **	–	–	–	–	–	0,21
ОРТ непродовольственными товарами	0,17 **	0,16 *	–	–	–	0,22 *	0,16	–	–
Объем платных услуг населению	–	0,12	–	0,23 **	0,18 *	–	–	–	–
Объем работ по ВЭД «Строительство»	–        –        –			–       –       –        –				0,22 ***       –
Изменение валютного курса рубля	0,06	–	–	–	–	–	0,12 *	0,32 ***	0,20
AR -параметр	0,83	0,87	0,86	1,00	1,00	1,00	1,00	1,00	1,00
Показатели качества модели
2 R adj	0,97	0,94	0,95	0,72	0,70	0,78	0,76	0,87	0,72
MAPE , %	1,2e-16	1,7e-16	0,6e-16	1,2e-15	1,1e-15	1,5e-16	9,9e-16	1,3e-13	1,9e-14
AIC	–1,07	–0,84	–0,92	–1,51	–1,46	–1,65	–1,64	–6,18	–5,30
BIC	–0,84	–0,65	–0,74	–1,37	–1,33	–1,47	–1,46	–6,04	–5,12
Источник : рассчитано автором.
Примечание : «–» – невключение в		модель фактора, U		- значимость		коэффициентов на		0,001 %-м	уровне,
U“ - на 0,01 %-м, u * - на 0,05 %-м, U		– на 0,1 %	м.

Самые удачные спецификации, оцененные модификациями метода Чоу–Лина и методом Литтермана, представлены в табл. 2, но в нашем случае модели 8–16 по качеству (на основе R _a ² _dj , MAPE ) уступают моделям, оцененным классическим методом Чоу–Лина.

Таким образом, лучшей признана спецификация 6, которая содержит в качестве индикаторных переменных показатели как Росстата, так и мониторинга предприятий Банка России: ИПП по ВЭД «Добыча полезных ископаемых» и «Обрабатывающие производства»; ОРТ непродовольственными товарами; изменение валютного курса рубля. Поскольку оценки модели получены методом Чоу–Лина с нулевым коэффициентом авторегрессии остатков, они совпадают с оценками, выявленными с помощью метода наименьших квадратов.

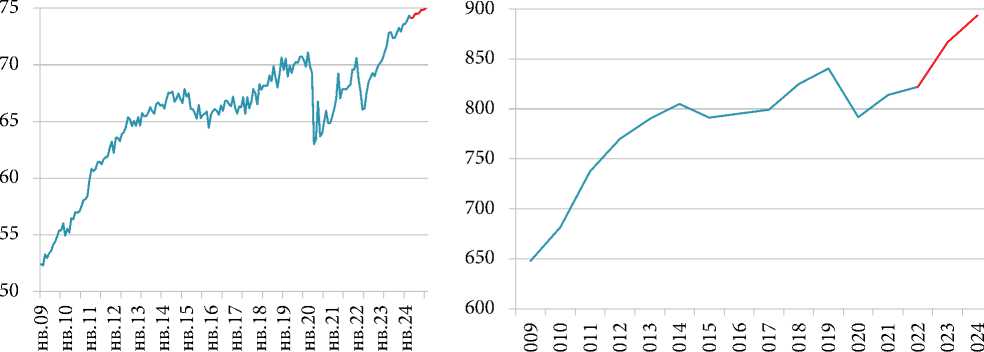
На основе выбранной спецификации произведена оценка высокочастотного ряда, который и представляет собой опережающий индикатор ВРП (рис. 3, а ). Агрегированные значения индикатора, полученные суммированием ежемесячных значений внутри одного года, обеспечивают хорошую аппроксимацию годовых значений ВРП (рис. 3, b ). Средняя абсолютная ошибка внутривыборочного прогноза ( in-sample forecast ) близка к нулю (см. табл. 1), что свидетельствует о высокой надежности полученных результатов.

На следующем шаге для полученного высокочастотного ряда осуществлялась разработка

Источник : составлено автором.

Рис. 3. Низкочастотная и высокочастотная динамика опережающего индикатора ВРП и ее прогноз, в сопоставимых ценах 2009 г., млрд руб.: а – ежемесячная динамика; b – годовая динамика

Fig. 3. Low-frequency and high-frequency dynamics of the leading indicator of GRP and its forecast, in comparable prices of 2009, billion rubles: а – monthly dynamics; b – yearly dynamics

прогнозной модели. Для моделирования был использован класс моделей ARIMA ( p , d , q ). По результатам эконометрического моделирования для опережающего индикатора из нескольких альтернативных моделей выбрана модель ARIMA (2, 1, 3) (табл. 3), обладающая наименьшей ошибкой внутривыборочного прогноза MAPE , равной 0,90 %, и наименьшими значениями информационных критериев.

Табл. 3 . Результаты оценивания модели ARIMA (2, 1, 3) для опережающего индикатора ВРП

Table 3. Estimation results of ARIMA (2, 1, 3) for the gross regional product leading indicator

Член модели	Значение коэффициента
Свободный	0,12 *
AR (1)	–1,04 ***
AR (2)	–0,89 ***
MA (1)	0,81 ***
MA (2)	0,65 ***
MA (3)	0,31 ***
Источник : рассчитано автором. Примечание : U *** - значимость коэффициентов на 0,001 %-м уровне, U * - на 0,05 %-м.

Как видно из табл. 3, все включенные в модель члены являются статистически значимыми по t-критерию. Разработанная модель признана адекватной, поскольку остатки являются «белым шумом», а корни характеристического уравнения AR-части лежат внутри единичной окружности, что свидетельствует о ее стационарности. Прогнозные значения, полученные на основе модели ARIMA, также представлены на рис. 3. Важно отметить, что горизонты прогноза для ВРП и его опережающего индикатора отличаются и связано это с двухлетним запаздыванием публикации значений ВРП (см. графики на рис. 3). Так, значения опережающего индикатора ВРП получены по модели 6 на основе доступных на момент анализа оперативных данных (до апреля 2024 г.), а его прогноз осуществлялся по модели ARIMA до декабря 2024 г. Посредством агрегации ежемесячных значений опережающего индикатора ВРП в годовые получен прогноз ВРП на 2023– 2024 гг., в соответствии с которым темп прироста ВРП (в сопоставимых ценах в процентах к предыдущему году) оценивается в 45 % в 2023 г. и 3 % в 2024 г. По мере поступления оперативных данных за последующие месяцы года прогноз может корректироваться.

Анализ качества вневыборочного прогноза ( out-of-sample forecast ) ВРП (на основе MAPE , %) с использованием моделей темпорального дезагрегирования и ARIMA производился в сравнении с «наивной» моделью 1 (т. е. моделью случайного блуждания без дрейфа) методом расширяющегося окна, который показал, что, во-первых, качество вневыборочного прогноза по предложенной методике превосходит качество «наивного» прогноза и, во-вторых, с периодом упреждения до двух лет качество вневыборочного прогноза можно считать приемлемым ( MAPE менее 5 %). Это позволяет рекомендовать модель темпорального дезагрегирования к использованию для оценки и краткосрочного прогноза опережающего индикатора ВРП.

ЗАКЛЮЧЕНИЕ

По итогам проведенного исследования можно утверждать, что методы темпорального дезагрегирования могут эффективно применяться для разработки высокочастотного опережающего индикатора для регионального выпуска. Проведенный эмпирический анализ данных с 2009 г. по Республике Башкортостан позволил оценить ненаблюдаемый опережающий индикатор ВРП (сезонно сглаженный),