Определение оптимальных параметров замеса сбивного полуфабриката из смеси ржаной и пшеничной муки

При механическом разрыхлении теста важным является выбор оптимальных параметров замеса сбивного полуфабриката. Цель исследования – выбор режима приготовления теста из смеси ржаной и пшеничной муки, определение оптимальных значений частоты вращения вала сбивальной машины, давления подаваемого атмосферного воздуха в камеру, продолжительности сбивания полуфабриката.

Тесто из смеси ржаной (60 %) и пшеничной муки (40 %) влажностью 54 % замешивали на экспериментальной установке периодического действия, разработанной на кафедре технологии хлебопекарного, макаронного и кондитерского производства.

Основными факторами, влияющими на показатели качества теста, были выбраны: X 1 (3 – 9 мин)– продолжительность сбивания, X 2 (400 – 500 мин^-1) – частота вращения месильного органа и X 3 (0,2 – 0,4 МПа ) – величина давления сжатого воздуха.

Соотношение ржаной и пшеничной муки 60 на 40 % выбрано в связи с тем, что повышение кислотности теста (с увеличением дозировки ржаной муки) способствует пептизации белков и одновременному набуханию, улучшению реологических свойств ограниченно набухшей части белков, но при дальнейшем увеличении дозировки ржаной муки, начиная с 70 %, наблюдается повышение объемной массы, увеличение эффективного

коэффициента сопротивления. Вероятно, это связано с разрушением частиц растворимых слизистых веществ ржаной муки и преобладающей части нерастворимых (набухших) частиц, которые, расщепляясь, образуют комплексы с белками и тем самым приводят к снижению скорости диффузии молекул в поверхностный слой и увеличению вязкости и объемной массы полуфабриката [1].

Из ранее проведенных экспериментальных исследований влажность теста составляла 54 %. Пределы изменения фактора времени сбивания теста 3-9 мин выбраны в связи с тем, что при сбивании теста менее 3 мин под избыточным давлением происходит насыщение системы воздухом, агрегирование набухших макромолекул клейковинных белков и их отталкивание. При сбивании более 9 мин происходит разрушение пенообразной массы, приводящее к уменьшению удельного объема хлеба и увеличению объемной массы, т. к. кинетические препятствия для коагуляции в виде электростатического отталкивания частиц дисперсной фазы уменьшаются, что приводит к агрегативной устойчивости.

Интервал изменения величины давления сжатого воздуха от 0,2 до 0,4 МПа выбран, потому что при сбивании теста при давлении меньше 0,2 МПа образование пенообразной массы происходит достаточно медленно, и образуется неравномерно разрыхленная структура с уплотненным межпоровым пространством, а сбивание при давлении более 0,4 МПа

ВестникВГУИТ, № 3, 201 2 приводит к быстрому разрушению структуры, вызванному синерезисом.

Предел изменения частоты вращения месильного органа от 400 до 500 мин-1 выбран потому, что сбивание теста с частотой вращения месильного органа менее 400 мин-1 приводит к более длительному процессу образования тестовой массы с неразвитой структурой, а сбивание теста с частотой вращения месильного органа выше 500 мин-1 способствует уменьшению объема массы и образованию неравномерной структуры полуфабриката и изделия.

Все эти факторы совместимы и некорре-лированы между собой. Критериями оценки влияния параметров сбивания приняли объемную массу теста ( Y 1 , г/см³) и удельный объем хлеба ( Y 2 , см³/100 г).

Для решения задачи оптимизации и параметров замеса был реализован активный эксперимент по системе центрального композиционного униформ-ротатабельного плана, обеспечивающего получение одинаковой величины дисперсии выходного параметра для любой точки в пределах изучаемой области.

В результате статистической обработки экспериментальных данных получили уравнения регрессии, адекватно описывающие зависимости критериев оценки Y 1 , Y 2 от исследуемых факторов. Воспроизводимость опытов, значимость регрессионных коэффициентов и адекватность уравнений подтверждена статистическими критериями Кохрена, Стьюдента, Фишера.

Y = 0 , 501 - 0 , 019 X. - 0 , 01 X ₂ - 0 , 013 X,

^{1                           1             2               3} (1)

+ 0 , 013 X ² + 0 , 01 X ₂ ² + 0 , 008 X ₃ ²

• Y ₂ = 221 , 05 8 + 1 , 863 X 1 + 17 , 817 X ₂ + + 3 , 463 X ₃ - 17,409 X ² -15 , 393 X ₂ ² -

• - 13 , 209 X ₃ ² - 1 , 429 X 1 X ₂ - 1 , 667 X 1 X ₃ , ⁽²⁾

Анализ коэффициентов при линейных членах уравнений (1), (2) показал, что на объемную массу теста ( Y 1 , г/см³) наибольшее влияние оказывает время сбивания и величина давления подаваемого атмосферного воздуха, а удельный объем изделия ( Y 2 , см³/100 г) в большей степ ени зависит от частоты вращения месильного органа и величины давления подаваемого атмосферного воздуха.

Для поиска оптимальных значений независимых переменных X1, X2, X; , при которых достигается минимальное значение Y1, соста-

вим систему уравнений: —L = -0,019 + 0,026X = 0 dX1                     1 dY1- = -0,01 + 0,02 X2 = 0 dX2                2 dY. —1 = -0,013 + 0,016 X3 = 0 dX3                   3 решением которой являются следующие значения: X1*= 0,73, X,*=0,5, X;*=0,81.

Аналогично находим оптимальные значения независимых переменных X 1 , X 2 ,X ; , при которых достигается минимальное значение Y 2 :

dY ² = 1,863 - 34,818 X - 1,429 X, - 1,667 X₃ = 0

dX1                       1            23

dY.

^Y = 17,817 - 30,786 X ₂ - 1,429 X. = 0

dX 2                      21

dY.

• ²    = 3,463 - 26,148 X ₃ -1,667 X₃ = 0

_ dX3                        33

Решением являются значения X 1 * = 0,024, X>*=0,57, X _; * =0,13.

Анализ результатов проведенной оптимизации показал, что оптимум по Y 1 не совпадает с оптимумом по Y 2 .

Для поиска компромиссного решения (поиска условий одновременно удовлетворяющих Y। и Y2) была поставлена задача оптимизации методом перебора на равномерной сетке. В ходе решения осуществлялся расчет значений выходных параметров Y1, Y2 в диапазоне изменения входных переменных:

• 3    <  X 1 < 9 мин;

400 <  X 2 < 500 мин^-1;

0,2< X _;< 0,4 МПа.

В результате расчетов найдены оптимальные значения параметров: X 1 = 6,5 мин; X 2 = 470 мин^-1; X _;=0,35 МПа, которые обеспечивают максимальное значение удельного объема Y 2 = 218 см³/100 г и минимальное значение объемной массы теста Y 1 = 0,48 г/см³, что гарантирует получение сбивного теста с лучшими характеристиками качества.

Проведем проверку найденных оптимальных параметров, оценку степени точности и надежности полученных значений параметров оптимизации. При оптимальных значениях X 1 , X 2 , X ; были изготовлены образцы изделий

( n = 10 шт.), для которых определяли объемную массу теста и удельный объем хлеба.

В таблице представлены средние арифметические значения указанных параметров у^э и дисперсии S, полученные по результатам 10 параллельных опытов. Как видно из таблицы расчетные и экспериментальные значения параметров оптимизации несколько отличаются друг от друга.

Для того чтобы эти различия признать несущественными и объяснить только случайной ошибкой, была выдвинута нуль-гипотеза о том, что расчетные и экспериментальные значения каждого параметра оптимизации принадлежат к одной и той же генеральной сово-

Для проверки выдвинутой нуль‒гипотезы воспользуемся распределением Стьюдента. При этом для каждого параметра оптимизации вычисляем расчетное значение критерия Стьюдента (см. таблицу)

t p

I у ’ - у p l

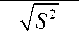
Сравнение каждого значения tp с табличным tm = 2, 29 (при числе степеней свобо ды ^ = 9 и принятой доверительной вероятности Y = 95 % ) показывает для каждого параметра оптимизации tp < tm.

купности.

Таблица 1

Результаты проверки оптимальных параметров

Параметр оптимизации	Значение параметра оптимизации		Дисперсия S 2	Расчетное значение критерия Стьюдентa tp	Ошибкa 5	Доверительный интepʙaл
	Рaсчетное У	Эксперимен-тaльное y э
Объемʜaя мaссa теста Y 1, г/см3	0,489	0,448	0,0049	1,823	0,05	0,439-0,539
Удельный объем хлеба Y 2 , см3/100 г	218,331	217,15	3,42	2,011	1,34	216,991 219,671

Это указывает на то, что выдвинутая нуль-гипотеза может быть принята, т. е. различия между расчетным и экспериментальным значениями каждого параметра оптимизации следует признать несущественными (с доверительной вероятностью 95 %)и объяснить только случайной ошибкой.

Результаты вычислений по каждому параметру оптимизации представлены в таблице в виде доверительных интервалов y^p ± 5 при принятой доверительной вероятности у = 95 %.

Как видно из таблицы, экспериментальные значения параметров оптимизации не выходят из-за границы соответствующих доверительных интервалов, полученных расчетным путем, что указывает на достоверность и надежность результатов.

Таким образом, было установлено влияние параметров замеса (давление сжатого воздуха, частота вращения месильного органа и продолжительность сбивания теста) на показатели качества сбивного полуфабриката из смеси ржаной и пшеничной муки. В результате статистической обработки экспериментальных данных получены математические и графиче- ские зависимости исследуемых характеристик теста от изучаемых факторов.

На основании уравнений определены оптимальные параметры замеса, которые могут быть рекомендованы при производстве сбивного хлеба из смеси ржаной и пшеничной муки требуемого качества.

Правильность выбора оптимальных значений приготовления сбивного полуфабриката подтвердили серией параллельных экспериментов, которые показали сходимость результатов.