Оптимальное по быстродействию кинематическое управление стыковкой твердых тел во вращающейся системе координат

Проводится обобщение задачи оптимального по быстродействию кинематического управления стыковкой двух твердых тел, рассмотренной в работе [1], на случай движения твердых тел во вращающейся системе координат, что представляет интерес при исследовании оптимальных движений пространственных механизмов, оптимальных условий стыковки космических аппаратов, при управлении манипуляционными роботами и т.д. Для определения времени быстродействия, траекторий оптимального движения и управляющих функций применяются аппарат кватернионов и бикватернионов, методы винтового исчисления и принцип максимума Л.С. Понтрягина.

1.    Постановка задачи оптимального управления

Рассматривается задача оптимального по быстродействию управления стыковкой двух твердых тел во вращающейся системе координат, когда в конечный момент времени

происходит совпадение систем координат, неизменно связанных с телами. Пусть опорная система координат I совершает вращение с угловой скоростью го * = го * ( t ) относительно инерциального пространства. Тогда кинематические уравнения, описывающие перемещения твердых тел 1 и 2, имеют вид

^{2 X} k = ^X к ° ^го к ^{- го} * ° ^х к ,                    ₍₁₎

2 X 0 = X_k ° и_к + X 0 ° го_к - го * °Х 0 , к = 1,2.

Здесь Xk + s Xk - бикватернионы, опре- деляющие положение связанных с телами систем координат E и E относительно опорного базиса I, s – символ Клиффорда, (s2 = о). Кватернионы Хк характеризуют ориентацию твердых тел в опорной системе координат; Xок =1 rk ° Xк =1 rk ° Xк , где rk, r'k - гиперкомплексные отображения радиус-векторов, соединяющих начала опорной и связанных систем координат, на опорный и связанный базисы соответственно. ω , υ – гиперкомплексные отображения векторов угловой и поступательной скоростей на связанные с твердыми телами базисы E и E .

Начальные положения твердых тел задаются равенствами

X k ( 0 ) = I k 0 , I k ( 0 ) = I k 0 , k = 1,2,      (2)

а конечное положение (совпадение систем координат E и E ) определяется условиями

X , ( T ) = ± X ₂ ( T ) , l 0 ( T ) = ± X 0 ( T ) , k = 1,2. (3)

На угловые и поступательные скорости наложены ограничения

|| ^Ю k 11 = ® H + ^ k 2 + ^a k 3 - a k ,

|| U k || = Ц 2 + ^U k 2 + U 2 <  b 2 ,         (4)

a _k , b_k = const >  0, k = 1,2.

Требуется найти управляющие функции a kj , u kj ( k = 1,2, j = 1, 2, 3 ) , удовлетворяющие кинематическим уравнениям (1), ограничениям (4) и минимизирующие время перемещения твердых тел из начального положения (2) в конечное (3).

q k = vect ⁽ ~ k ° v k ) , ^k = 1,2.         ⁽⁸⁾

Используя полученные соотношения, найдем

2 ^q k =^{- w} k ° ~ k ° v k + ^x k ° ^w * ° v k + + sqal ⁽ w k ° ~ k ° v k + X k ° w * ° v k ) +

—

~

+ X

■ k ° v k ° ^w k

sqa^{l ( X} k ° v k

= [ ~ k ° v k

—

~

—

X _k ° w

° ^w k

~

—

—

w _k °

[ ~ k ° v k

*

° v k

X _k ° w

*

sqa^{l ( X} k ° v k ^)]

—

—

° v k ) =

° ^w k

—

sqa^{l ( X} k ° v k ^)] =

= q k ° ^w k ^{— w} k ° q k , k = 1,2.

2. Построение оптимального решения

Воспользуемся принципом максимума Л.С. Понтрягина [2]. Введем в рассмотрение кватернионы ψ , ψ _k ⁰ , соответствующие кватернионам λ , λ _k ⁰ , и составим функцию Гамильтона – Понтрягина:

H = Z sqa^{l ( X} k ° v k + ^X k ° ~ k ) = k = 1

= -Z sqa^{l ( X} k ° ^w k ° v k - ^w * ° ^X k ° v k +

² k = 1

+ X^ ° U_k ° v ⁰ + X ⁰ ° w_t ° v ⁰ - w * ° X ⁰ ° v ⁰ ) .

kk   k   k   k   k       k   k

Следовательно, qk = qkx wk, k=1,2.           (9)

Аналогичным образом получаем pk = pkx wk + qkx Uk, k=i,2-     (10)

Из условия максимума функции Гамильтона – Понтрягина (6), соотношений (5)– (10) следует, что оптимальные управления wj, u_t ( k = 1,2 ) выражаются теми же формулами, что и в случае неподвижной опорной системы координат [1], а именно

w 1 = a 1 Z , w ₂ =- a ₂ Z ,          (11)

U 1 = b 1 X 1 ° Z ° X 1 ,   u ₂ =— b ₂X₂ ° Z ° X ₂,  (12)

где ζ и ξ – единичные, постоянные по направлению векторы.

Подставим выражения (11), (12) в уравнения (1) и найдем решение этой системы дифференциальных уравнений при начальных условиях (2). Получаем

Выпишем сопряженную систему дифференциальных уравнений

2 ^v k = v k ° ^w k ^{— w} * ° v k ⁺ v k ° ^U k , 2v k = v k ° w k - w * ° v k , k = 1,2

и преобразуем функцию H 1²

H =   ,Z sq^{al ( w} k ° p k + ^u k ° q k ^-

² k = 1                                    (6)

- ^w * ° ^x k ° ^v k ^{- w} * ° ^x k ° ^v k )•

X 1 = H ( t ) ° Xw ° exp f X 2 = p ( t ) ° X 20 ° exp ^-	a i t J z 1 ’
	a 2 1Д " T z J ’	(13)
Xj1 = p ( t ) ° Vj ( t ) ° exp	f a 1 1 й 1 z J ’	(14)
X 0 = H ( t ) ° V 2 ( t ) ° exp f	a 2 1 z0 - T z J ’

Здесь так же, как и в работе [1], введены обозначения pk = vect(~k ° vk + X0 ° vk),        (7)

где

V 1 ( t ) = 1 b 1 J [ X ( t ‘ ) ° Z ° m ( t ‘ ) ° X 10 ] dt ‘ + X 00 ,

V 2 ( t ) = - 1 b 2 J [ X ( t ‘ ) ° Z ° m ( t ') ° X 20 ] dt ‘ + X 00 ,

г

p ( t ) - решение кватернионного уравнения

2р = - ст * ° р ,

удовлетворяющее   начальному   условию

р ( 0 ) = 1 , в частности, если вектор ст * ( t ) име-

ет постоянное направление, то

(

Н ( t ) = exp --[ ст * ( т ) d r .

х 2 0           7

Используя граничные условия (3) и равенства (13), (14), найдем оптимальные по быстродействию время T взаимной переори-

exp

х

1 ^t

“7J ^ст * ^{( т} ) d ^T

Т

х

1 cos

t ₁

I ш * d r , 0, sm — 0²

t

J ш * d r , 0 .

ентации твердых тел, время T , при котором

начала систем координат E и E совпадают,

и векторы ζ , ξ :

T = —-—arccos |sqal(~[0 ° X20)| a+a2        1                1

^T2 = ,     ,   ^ 20 ° ^ 20 ^X 10 ° ^X 10

b l + b 2¹

^ _{= ±} vect ( ~ 10 ° ^X 20 ) | vect ^(x _w ° X 20 )|

§=

^X 20 ° ^X 20 ^X 10 ° ^X 10

^X 20 ° ^X 20 ^{- X} 10 ° ^X 10

В формуле (17) следует брать верхний знак, если sqal ( ~ ₀° X₂₀) > 0 , и нижний, если sqal ( Zj₀ ° X₂₀) < 0 .

Из полученных соотношений вытекает, что оптимальная по быстродействию стыков-

ка твердых тел осуществляется за время T = max (T, T2 ), где T и T вычисляются по формулам (15), (16). Векторы оптимальных управлений ω и иk (k = 1,2) находятся из соотношений (11), (12), (17), (18) при t e[0,T ] и t e[0, T ] соот

Оптимальное по быстродействию перемещение твердых тел из начального положения

X ₁₀ = ( 0.001; 0.2; 0.5; 0.8426 ) ,

X 00 = ( - 0.5; - 0.1;0.041;0 ) ,

X 20 = ( 1;0;0;0 ) , X 2o = ( 0;0;0;0 )

в конечное состояние (3), при ax = 2, a2 = 1, b = 0.5, b2 = 0.1, ш* = 1, осуществляется за время T = T2 = 1.7052 . Графики функций Akj(t), А0(t) (k = 1,2, j = 0,1,2,3) изображены на рис. 1–2, компоненты угловых скоростей определяются равенствами ш11 =-0.4, ш12 =-1, ш13 =-1.6852, ш21 = 0.2, ш22 = 0.5, ш23 = 0.8426, а графики изменения компонент поступательных скоростей и(t), u2J(t)(j = 1,2,3) представлены на рис. 3. В момент времени T = 1.0465 происходит совпадение ориентаций систем координат E и E относительно неподвижного базиса, в этот момент времени X1( T )= X 2 (T1 )=(0.1238;0.8751;-0.4147;-0.2164 ). При t g[T, T] осуществляются только поступательные перемещения твердых тел при неизменной ориентации, в течение этого времени Л j (t)=4 j (T1)=Л2 j (t)=4 (T)   (j = 0,1,2,3),

Ш] ( t ) = 0 ( j = 1,2,3 ) . В конечный момент времени t = T происходит совпадение начал систем координат E и E , при этом

X 0 ( T ) = X 0 ( T ) = ( 0.0821; - 0.0159; - 0.0140; 0.0093 ) .

ветственно; причем ю₄ = 0 на промежутке [ T , T ] , если T <  T и U = 0 на промежутке [ T 2 ,T 1 ] , если T 2 <  T .

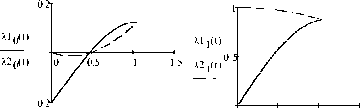
0       0.5       1        1.5

Пример 1

Рассмотрим случай, когда опорная система координат I является орбитальной [3], что представляет интерес при исследовании оптимальных условий стыковки космических аппаратов. Тогда ст * ( t ) = ш * ( t ) • i₂ и

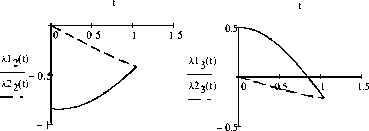
t

t

Р ис. 1. Графики функций 4 ( t ) и А, ( t ) ( j' = 0,1,2,3 )

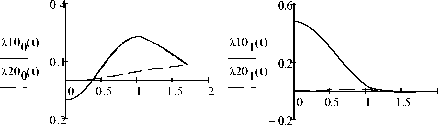
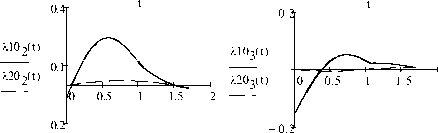
Рис. 2. Графики функций ^ ( t ) и ^ ( t ) ( j = 0,1,2,3 )

^ _    vect ( ^Z 10 ° ^Z 20 )

I vect ⁽ ~ю ° ^Z 20 )| ’

ζ ⁰

_{= ±} vect ⁽ ~ 10 ° ^z 20 ) _х | vect ⁽ ~ 10 ° ^z 20 )|

^{Х [ sqal ( Z} 10 ° ^Z 20 ^{+ Z} 10 ° ^Z 20 ^{) sqal ( Z} 10 ° ^Z 20 ^)] ± vect ^{( Z} 10 ° ^Z 20 ^{+ Z} 10 ° ^Z 20 )

I vect ⁽ ~ 10 ° ^Z 20 )|

Zj = ^ ( t ) ° Zj₀ ° exp

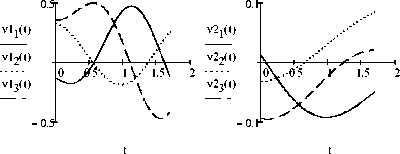
Рис. 3. Графики функций ц ( t ) и и₂ ( t ) ( j = 1,2,3 )

3.    Применение принципа перенесения Котельникова – Штуди

Рассмотрим задачу оптимального по быстродействию кинематического управления стыковкой твердых тел во вращающейся системе координат, для случая, когда поступательные скорости тел 1 и 2 не ограничены, а угловые скорости удовлетворяют ограничениям (4).

Применим принцип перенесения Котельникова – Штуди [4] к соотношениям (11), (13), (15), (17), определяющим оптимальную по быстродействию ориентацию твердых тел. Заменим кватернионы Z, ^, Z_k о, ^wt ( k = 1,2 ) на соответствующие им бикватернионы Z + s Z ⁰, Z k + s Z k , Z k 0 + s z k 0 , © k + s и k ( k = 1,2 )

и максимальные модули угловых скоростей a k ( k — 1,2 ) на дуальные модули a_k + sa ⁰ ( k = 1,2 ) кинематических винтов твердых тел 1 и 2. После "развертывания" полученных соотношений по правилам винтового исчисления [4], найдем искомые управляющие функции, траектории движения и время быстродействия

Z2 = g(t)° Z20 ° exp I —

z0 = Xt)° z00 ° exp [ atZ] +

\ 2

^{+ z} 10 ° ^еД at ^Z j t ⁽ a ^{0 Z + a} 1^Z ° ) , ^z 2 = H ⁽ t ) ° ^z 20 ° ^exP ⁽ aY ^{Z j}

• ^{— z} 20 ° exp ^(— О ^{2 Z j} t ⁽ a ^{0 z} + a 2 ^{z 0} )

T = —-— arccos I sqal(~j0 ° Z20)|, ax + a2          11

0    0 _ — ^{2sqal ( Z} 10 ° ^z 20 + ^Z 10 ° ^z 20 )

a + a 2 — т       i------------j----------- .

T jl — sqal² ( ~ 10 ° Z 20 )

Верхний знак в выписанных формулах соответствует sqal ( ~₁₀ ° Z ₂₀ ) > 0 , а нижний -sqal ( ~₁₀ ° Z ₂₀ ) < 0 .

Пример 2

Перемещение твердых тел из начального положения

Z_o = ( 0.001; 0.2; 0.5; 0.8426 ) ,

Z 0 = ( — 0.5; — 0.1; 0.041; 0 ) ,

Z 20 = ( 1;0;0;0 ) , Z 20 = ( 0;0;0;0 )

в конечное состояние (3), при a_l — 2, a ₂ — 1, ш * — 1 , осуществляется за время T — 1.0465 при тех же значениях угловых скоростей

® 1 J ( t ) , ^ 2 J ( t ) ( J = ^{1,2,3 )} , что и в примере 1 и следующих значениях компонент векторов поступательных скоростей твердых тел 1 и 2:

U = 0.1002, u ₁₂ =- 0.3315, u ₁₃ =- 0.4205, u ₂₁ =- 0.009, u ₂₂ = 0.2685, u ₂₃ = 0.3834.

Параметры кинематических винтов соответ- ственно равны — = 0.25, — = 0.4555. Зави- a1           a2

симости Akj(t), (k = 1,2, J = 0,1,2,3) те же, что и на рис. 1 примера 1, зависимости ^kj(t) (k = 1,2, J = 0,1,2,3)   изображены на рис. 4. В конечный момент времени

X! ’ ( T ) = X 0 ( T ) =

= ( 0.0944; - 0.0414; - 0.1462;0.1666 ) .

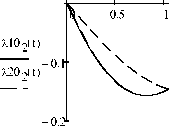
t

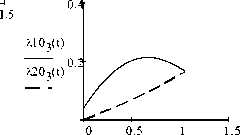
Рис. 4. Графики функций ^_} ( t ) и ^ ( t ) (j' = 0,1,2,3 )

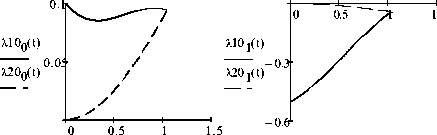
Заключение

В кинематической постановке рассмотрена задача оптимального по быстродействию управления стыковкой двух твердых тел во вращающейся системе координат. На основе принципа максимума Л.С. Понтрягина найдено оптимальное решение задачи в предположении, что угловые и поступательные скорости тел ограничены, а при помощи принципа перенесения Котельникова – Штуди – для случая, когда поступательные скорости объектов не ограничены, а угловые скорости ограничены по модулю. Полученные результаты представлены в кватернионной форме. Рассмотрены конкретные примеры, в которых, при заданных граничных условиях, осуществляется построение оптимального решения.