Оптимизация управляющих воздействий в рецептурах колбасных изделий при наличии технологических дефектов

При корректировке технологических дефектов в рецептурах колбасных изделий (например, в рецептуре содержится в значительном количестве мясное сырье с пороком автолиза-PSE,RSE или DFD, мясo птицы механической обвалки (ММО), жиросодержащее сырье и т.п.) , как правило, известен перечень функционально-технологических свойств, которыми должна обладать эта рецептура. Этот набор свойств формируется за счет управляющих воздействий в виде пищевых добавок с заданными функциональными свойствами [1-4]. В результате возникает задача подбора перечня управляющих воздействий (в виде пищевых добавок), который в сумме содержал бы нужный набор ингредиентов, но при этом суммарная стоимость единицы массы этих добавок была бы минимальна.

Математическая постановка задачи

Рассмотрим формальную постановку этой задачи. Пусть дано множество пищевых добавок Mpd, каждый элемент которого Mpd(i) задан в виде кортежа:

Mpd(i) =

1, если добавка Mpd(i) обладает где Mpd(i,k) =

k-тым функциональным свойством,

0, в противном случае k = 1,..K, где K – количество функциональных свойств,

Mpd(i,K+1) – цена единицы массы добавки i.

Пример такого множества представлен в таблице 1.

Пусть задан также требуемый набор функциональных свойств в виде вектора:

FS = , l=1,..L, L ≤ K

1, если требуется наличие функ-

FS(l) = ционального свойства l,

Таким образом, вектор FSp представляет собой весь набор функциональных свойств, соответствующих подмножеству Ppd.

Требуется определить такое подмножество Ppd, при котором:

Fp(Ppd) = FS (2)

|Ppd | и критерий Q = ∑Ppd(i,K + 1)- > min (3) i=1

Алгоритм решения задачи

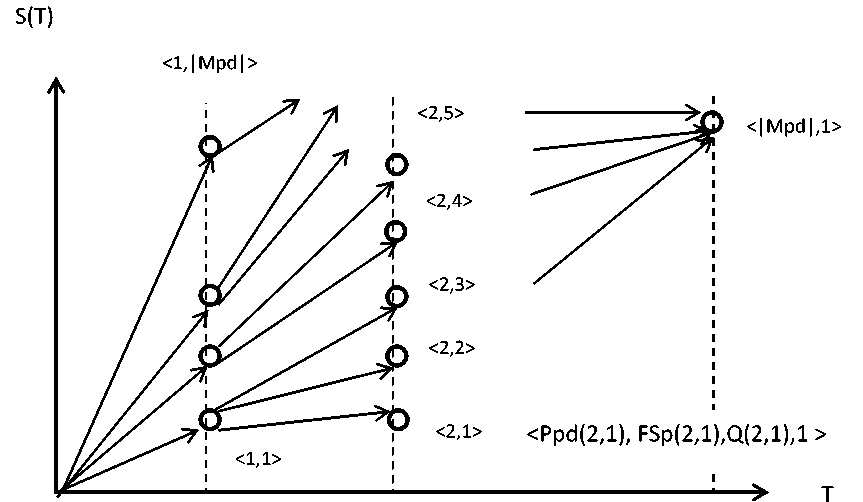
Данная задача относится к комбинатор- ным задачам целочисленного программирования. Рассмотрим процесс пошагового построения решения этой задачи (см. рисунок 1) на плоскости , где Т=0,..|Mpd|, S(T) – множество точек, каждой из которых соответствует тройка: , опи- сывающая варианты построения решения на шаге Т.

Здесь nom(T-1) – номер точки предыдущего шага, из которой получена точка на шаге Т.

Процесс начинается с точки <0,0>, Ppd(0) =

∅ ,

FSp(0)=<0,…0>,Q(0)=0. На первом шаге получаем |Mpd| вариантов формирования множества Ppd, каждое из которых состоит из одного объекта множества Mpd: Ppd(1,1), Ppd(1,2),… Ppd(1,|Mpd|). На втором шаге получим С² |Mpd| вариантов, на третьем С³ |Mpd| вариантов, на последнем – С^|Mpd| |Mpd|. Такое построение представляет собой прямой перебор вариантов решения задачи. Сопоставим каждой точке плоскости

вершину некоторого графа, а получение одного варианта решения на каждом шаге построения решения представим дугой графа. Полученный граф будем называть графом допустимых состояний (ГДС). Для уменьшения размерности задачи важно на каждом шаге отсеивать недопустимые и не перспективные варианты решений [5, 6].

Рассмотрим процесс получения новой точки S(T+1,n) из точки S(T,j).

Пусть Mpd(n) ∈ Mpd \ Ppd(T,j).

Образуем

Ppd(T+1,n) = Ppd(T,j) ∪ Mpd(n) (4)

0, в противном случае

FSp(T+1,n) = Fp(Ppd(T+1,n)) (5)

Пусть Ppd – некоторое подмножество Mpd:Ppd ⊆ Mpd. Определим оператор Fp, формирующий вектор FSp:

FSp = Fp(Ppd)           (1)

FSp(l) = 0 l=1,..L

FSp(l) = FSp(l) ∨ Ppd(i,l) l=1,..L, i =1,..|Ppd|

Если

FSp(T+1,n)=FSp(T,j)∨∃1(FSp(T+1,n,l)>FS(l)), (6) то добавление новой добавки либо не увеличило функциональные возможности нового подмножества, а стоимость набора увеличилась, либо новая добавка обеспечивает лишнее функциональное свойство. Такая вершина с к ГУИТ 4 2 15

будет считаться недопустимой для дальнейшего развития. В противном случае, новая вершина - допустима. Для допустимой вершины критерий Q(T+1,n), будем вычислять по следующему рекуррентному соотношению:

Q(T+1,n) = Q(T,j) + Mpd(n,K+1).   (7)

0             1                 2

|Mpd|

Рисунок 1. Пошаговое построение решения на плоскости состояний

Если

FSp(T+1,n) = FS,             (8)

то такая точка остается на вертикали Т+1 как допустимая и далее переходит на следующие уровни в таком же статусе.

Сопоставим каждой дуге перехода от точки к точке величину Mpd(n,K+1), которую будем интерпретировать как длину дуги. В таком случае решение нашей задачи сводится к нахождению кратчайшего пути на ГДС от вершины <0,0> до вершины <|Mpd|,1>.

Рассмотрим возможность уменьшения количества вершин ГДС на каждом шаге построения решения. Пусть Ppd(T+1) - множество всех допустимых точек, полученных на шаге Т+1. Рассмотрим две произвольные точки на вертикали Т+1: Ppd(T+1, i) и Ppd(T+1,J), соответствующие им векторы FSp(T+1, i) и

FSp(T+1, J), критерии Q(T+1,i) и Q(T+1,J).

Точка Ppd(T+1, i) является неперспективной по отношению к точке Ppd(T+1,J) если выполняется следующее соотношение:

V m ( Ppd ( T + 1, j , m ) >

Ppd ( T + 1, i, m) л Q ( T + 1, j ) <  Q ( T + 1, i)) ⁽⁹⁾

Смысл формулы (9) заключается в том, что на множестве Ppd(T+1,i) больше функциональных возможностей по сравнению с множеством Ppd(T+1,J) при меньшей суммарной стоимости добавок. Все неперспективные вершины на каждом шаге построения решения отбрасываются. Таким образом, укрупненный алгоритм решения нашей задачи представлен на рисунке 2.

В блоке 4 производится формирование множества допустимых вершин ГДС на вертикали Т в соответствии с формулами (4)-(7). В блоке 5 производится отсев неперспективных вершин ГДС в соответствии с формулой (8), а вершина, удовлетворяющая соотношению (8), остается в допустимых. В блоке 6 отсеиваются неперспективные варианты вершин ГДС в соответствии с формулой (9). В блоке 7 проверяется существование на вертикале вершины, для которой вектор FSP совпадает с вектором FS. Если такая вершина есть, то выдается оптимальное решение. В противном случае выдается сообщение об отсутствии решения.

Рассмотрим пример определения набора оптимальных пищевых добавок для случая, когда в рецептуре вареной колбасы «Столичная» содержится большое количество жиросодержащего сырья. Пусть набор состоит из шести пищевых добавок со следующими названиями торговых марок: «Тарипрот супер», «Эмульмикс», «Столичная комби», «Рот-ко-лор», «Росмикс система Жир E», «Росмикса-рома Столичная», свойства которых указаны в таблице 1 (0 – свойство в добавке отсутствует, 1 – свойство присутствует). Для решения проблемы связывания и эмульгирования жирного сырья, как ранее было показано, необходимы пищевые добавки, которые в комплексе содержали бы: фосфат (регулятор кислотности, водоудерживающий агент), антиоксидант, эмульгатор, загуститель, гелеобразователь, животный белок (наполнитель), краситель, фиксатор окраски, усилитель вкуса и аромата.

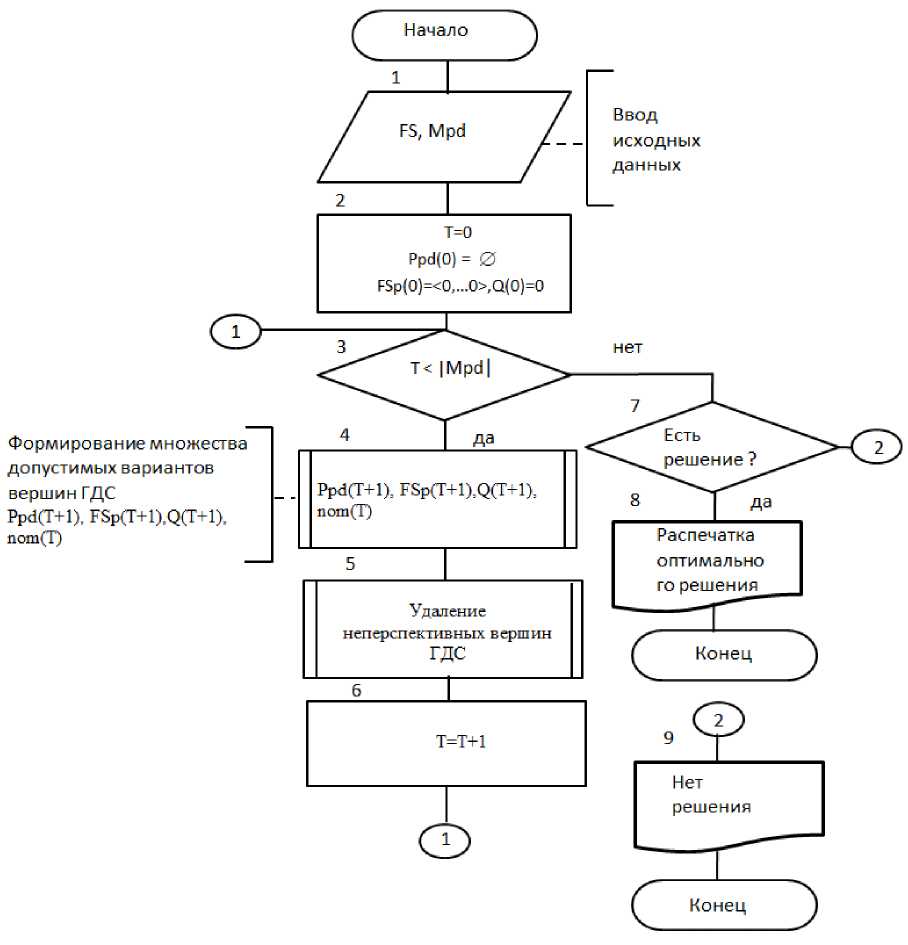
Рисунок 2. Укрупненный алгоритм решения задачи определения оптимального набора управляющих воздействий в виде пищевых добавок

Т а б л и ц а 1

Свойства пищевых добавок и их стоимость

Номер добавки	Пищевые добавки	Функционально-технологические и вкусоароматические свойства пищевых добавок
		Во-до-удержи-ваю-щие агент	Анти-оксидант	Эмульгатор	Загусти-тель	Геле-об-разо-ва-тель	Наполнитель	Краситель	Фиксатор окраски	Уси-ли-тель вкуса и аромата	Цена руб./кг
1	Тари-прот супер	0	0	0	1	1	0	0	0	0	360
2	Эмуль-микс	0	0	1	0	0	0	0	0	0	200
3	Столичная комби	1	1	0	0	0	0	1	1	1	330
4	Рот-ко-лор	0	0	0	0	0	0	1	0	0	265
5	Ро-смикс система Жир Е	1	1	1	1	1	1	1	1	0	306
6	Ро-смик-сарома Столичная	0	0	0	0	0	0	0	0	1	330

Необходимо определить, какие пищевые добавки включить в рецептуру, чтобы с одной стороны они, в конечном счете, содержали заданный набор указанных свойств, а с другой – их суммарная стоимость была минимальна. Решая данную задачу с применением рассмотренного выше алгоритма, получим, что оптимальным набором добавок будут: «Росмикс система Жир Е» и «Росмик-сарома Столичная» – они полностью покрывают множество. Этот набор содержит все необходимые ингредиенты для решения поставленной задачи, при этомих суммарная стоимость будет минимальная (636 руб/кг), в отличие от других возможных комбинаций.

Результаты и обсуждение

Рассмотренная постановка задачи и алгоритм ее решения позволил включить эту задачу в программный комплекс «"Мульти-Мит Эксперт"» [7] системы поддержки принятия решений экспертной системы для технолога мясоперерабатывающего предприятия. По своему классу она относится к комбинаторным задачам целочисленного линейного программирования. Предложенный алгоритм решения развивает идеи динамического программирования и позволяет отсеивать неперспективные варианты, используя рекуррентные соотношения на каждом шаге построения решения.

Выражаем благодарность ООО «Сириус» за финансовую поддержку при разработке экспертной системы «МультиМитЭксперт».