Организация обучения по дисциплине «Вычислительная математика» в дидактических системах нового поколения

virtual office, abilities, model of development of the student, the knowledge base, base of problems.

Современные процессы глобализации образования в мире предъявляют новые и более высокие требования к образовательной системе России. Всё более проявляется связь между степенью развития профессиональных компетенций человека и качеством его жизни. При этом профессиональные компетенции представителя современного российского общества могут способствовать не только эффективной реализации профессиональных функций, но и гарантировать успешную адаптацию личности в течение всей его активной жизни в социуме, поэтому, сегодня необходимо готовить инженера будущего, то есть инженера способного создавать инновационный продукт. Подготовить такого инженера, отвечающего требованиям стандартов третьего поколения, сложная педагогическая проблема. Для подготовки инженера будущего необходимы дидактические системы нового поколения, позволяющие сформировать специалиста на качественном уровне, в связи, с чем и внедряются в учебный процесс дидактические системы нового поколения, отвечающие требованиям ФГОС ВПО.

Рассмотрим проект дидактической системы нового поколения с виртуальной составляющей на основе, которой можно организовать обучение по дисциплине «Вычислительная математика» и подготовить инженеров способных к инноватике в данном направлении.

С развитием вычислительной техники появилась возможность обогатить содержание дисциплин, том числе и курса «Вычислительная математика», при помощи использования дидактических систем с виртуальными составляющими, например, внедрения в учебный процесс виртуального кабинета, который способен поддерживать курс, как в теоретическом, так и в практическом плане, а также такая система предоставляет новые возможности для быстрого развития способностей, поддержки эффективной деятельности и усвоения знаний студентов.

Виртуальный кабинет — это новое средство обучения, которое имеет определенную структуру, свои особенности сбора и организации информации. Структура определяется из целей и задач его использования.

Цели использования:

• •    представление материала в более наглядной и доступной форме;

• •    возможность учета индивидуальных способностей, потребностей, темперамента и занятости студента;

• •    создание психологических условий, способствующих лучшему восприятию и запоминанию учебного материала;

• •    облегчение процесса повторения и тренинга при подготовке к экзаменам и зачетам;

• •    полный контроль усвоения материала студентами и объективность их оценивания;

• •    экономия временных ресурсов, как преподавателя, так и студента.

• •    доступность изложенного материала 24 часа в сутки.

Задачи использования:

• 1)    поддерживать высокую учебную мотивацию студентов;

• 2)    формировать умение учиться – ставить цели, планировать и организовывать собственную учебную деятельность;

• 3)    поощрять их активность и самостоятельность, расширять возможности обучения и самообучения;

• 4)    развивать навыки рефлексивной и оценочной деятельности учащихся, формировать адекватную самооценку;

• 5)    содействовать персонализации образования; определять количественные и качественные индивидуальные достижения;

• 6)    создавать предпосылки и возможности для успешной социализации выпускников.

Структура кабинета представлена на рис. 1.

Виртуальный кабинет преподаватель — технолог, менеджер (администратор, тьютор)
Презентации Power Point Plash	Курс лекций	Курс лабораторных работ	Системы ди аг но стики С 0 СТО ЯН ИЯ к о м и ете н ц ии (те сты и а спо со 6иости, те сты н а з и ан ия)

УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ

Рис. 1. Структура виртуального кабинета

Как видно из рисунка 1, виртуальный кабинет по дисциплине «Вычислительная математика» имеет 4 составляющие:

• 1.    Комплекс презентаций по лекционному материалу

• 2.    Курс лекций

• 3.    Курс лабораторных работ

• 4.    Система диагностики состояния компетенции

На рис. 2 приведены эпизоды из презентаций дисциплины «Вычислительная математика».

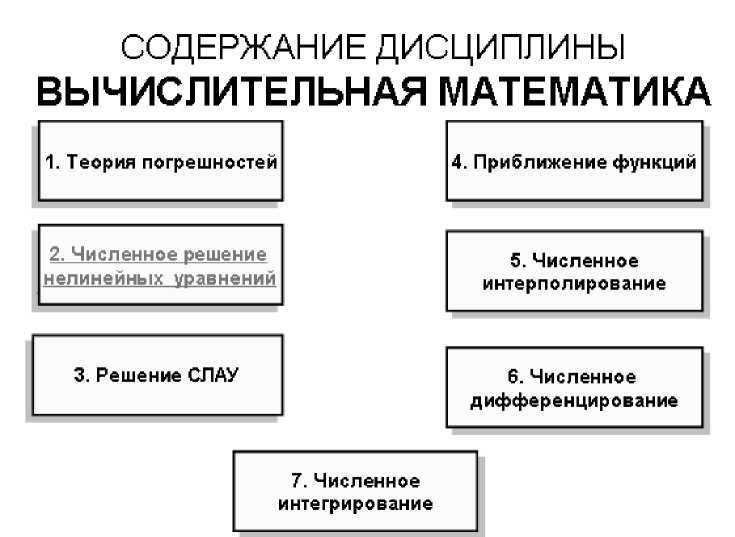
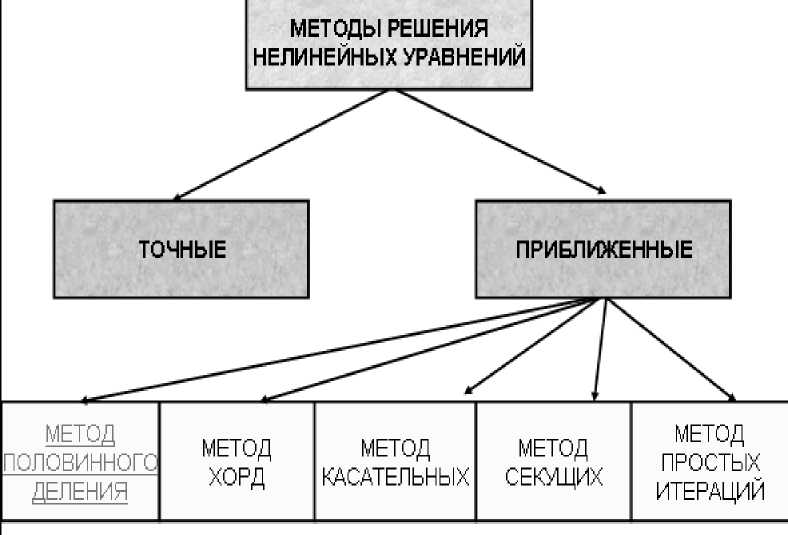
МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ

1.    ПОСТАНОВКА ЗАДАЧИ МЕТОДА2.    АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

Рис.2. Эпизоды из презентаций

Презентации созданы на основе лекционного материала, которые служат интерактивным подспорьем преподавателя для проведения лекционных занятий и самостоятельному усвоению материала студентами, они позволяют представить информацию более наглядно и сделать ее доступной для восприятия. На основе теоретического материала у студента выстраивается база знаний.

Как видно из рис.3, база знаний состоит из двух частей, которые постоянно находятся в непрерывной связи.

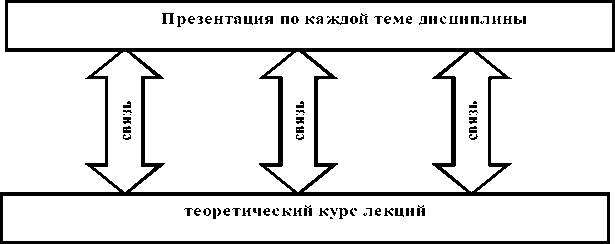
Рис. 3. Составляющие базы знаний дисциплины «Вычислительная математика»

Последовательно после усвоения единицы теоретического материала следует лабораторная работа, при выполнении которой необходимо воспользоваться полученной базой знаний.

Курс лабораторных работ имеет следующую структуру:

• ■    лабораторные работы по разделам курса, включающие последовательное описание их выполнения.

• ■    варианты, предлагаемые студентам для самостоятельного выполнения, в которых задания подобраны так, что позволяют или предполагают целенаправленно развивать способности студента и целенаправленно усваивать знания.

В начале каждой лабораторной работы преподаватель (исходя из актуального уровня развития обучающегося) строит упрощенную сущностную модель проблемы (прототип 0) с оценкой ее сложности, которая имеет единицу измерения р(час/раб), р – обратная величина показателя производительности труда преподавателя.

Производительность труда - плодотворность, эффективность производственной деятельности людей, измеряемая количеством продукции (благ и услуг), произведенной в единицу рабочего времени (час, смену, месяц, год), или величиной времени, затрачиваемого на единицу продукции. Производительность труда рассчитывается по формуле:

Поизводите льность труда = количество выпускаемой продукции время, необходимое для выпуска продукции Единица производительности труда – раб/час

• ■    Преподаватель полностью приводит решение прототипа 0 с подробными объяснениями.

• ■    Преподаватель строит последовательность прототипов, причем прототип 1 сложности р + ∆ р, получается путем валидации из прототипа 0 и т.д. Таким образом, вместо решения одной проблемы обучаемый решает последовательность прототипов проблем и тем самым он через «зоны ближайшего развития» доводит свой уровень развития до требуемого по ГОС ВПО уровня.

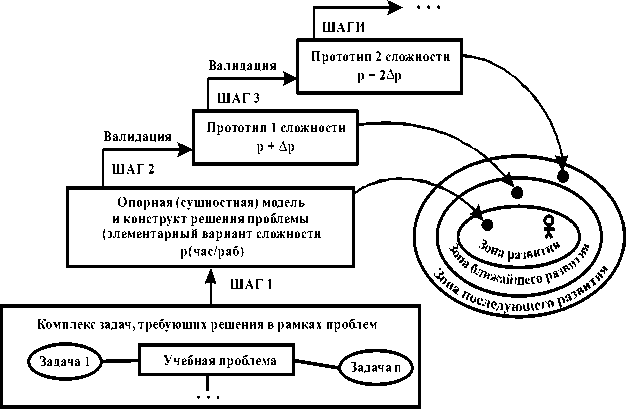
Рис. 4. Схема технологического маршрута при обучении с включением метода ОПОРНОЙ МОДЕЛИ и КОНСТРУКТА РЕШЕНИЯ в дидактический процесс

Таким образом, на основе изложенного теоретического материала, то есть по построенной базе знаний, перед студентом ставится база проблем, которые он должен решить.

Для того чтобы будущему инженеру решить поставленную перед ним проблему необходимо выполнить ряд требований:

• 1.    построить модель проблемы;

• 2.    построить алгоритм решения на основе модели проблемы и полученных знаний;

• 3.    реализовать алгоритм решения.

Для оценивания уровня способностей студента, на основании выполненных заданий, строится модель состояния развития каждого студента. При построении модели способности разделяются на три разновидности [1-3]:

А – формализационные – это способности человека, которые проявляются в фазах деятельности исследования аналогов проблемы и в фазах выбора аналога (творческого аналога) решаемой проблемы.

В – конструктивные способности (умение отобрать, создать, спроектировать) проявляются в фазах деятельности: в фазе выбора аналога, в фазе конструирования алгоритма решения проблемы. Конструирование в процессе обучения – средство углубления и расширение полученных теоретических знаний, и развитие творческих способностей, изобретательских интересов и склонностей учащихся.

С – исполнительские проявляются в фазе реализации решения проблемы.

Используя обратную величину производительности труда (Р), можно определить граничные точки модели состояния развития студента по метрикам А, В, С.

Причем метрики параметров А, В, С определяются исходя из методики основанной на акмеологическом подходе через следующий механизм рис.5.

Механизм оценки. Сравнении с показателями эксперта.

Сложность(проблема)=норматив(производительность раб/час) решение проблемы экспертом(р0(раб/час)

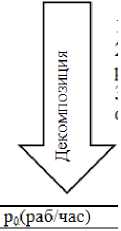
• 1    .Сложность формализации проблемы, т.е. A-сложность р_А=ар_а 2.Сложность конструирования решения проблемы, т.е. В - сложность Р.=РРа

• 3    .Сложность исполнения решения проблемы, т.е. С - сложность р_с=уро а+Р+у=1

I Рл(рзбчас) | р^раб час) | рс(раб.час)

Рис. 5. Модель оценки сложности проблемы

На рис. 6 изображена схема заданий лабораторных работ с оценкой сложности заданий.

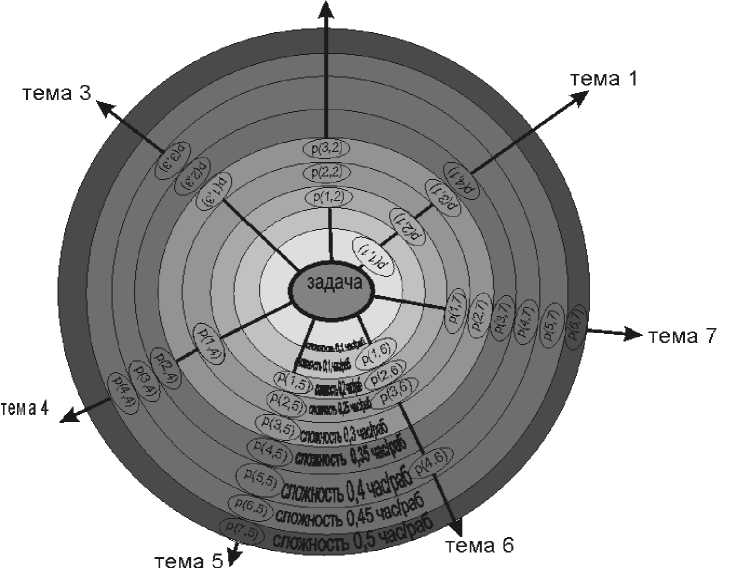
Рис.6. Оценка сложности заданий лабораторных работ по дисциплине «Вычислительная математика»

Показателями эффективности действия данного механизма формирования качеств будущего инженера на основе акмеологического подхода являются:

• •    высокая продуктивность деятельности;

• •    высокий уровень квалификации и профессиональной компетентности;

• •    оптимальная интенсивность и напряженность труда;

• •    высокая организованность;

• •    низкая опосредованность, зависимость от внешних факторов;

• •    владение современным содержанием и современными средствами решения профессиональных задач;

• •    стабильность высоких показателей деятельности;

• •    возможность развития субъекта труда как личности;

• •    направленность на достижение положительных социально–значимых целей.

После выполнения каждой лабораторной работы студент проходит тестирование на полноту и целостность полученных знаний.

На основе изученного лекционного материала и анализа результатов тестирований по каждой теме, можно определить граничные точки модели по метрикам POL(полнота знаний), CHL(целостность знаний), которые определяют эффективность деятельности студента по решению проблем.

Используя параметры метрик А, В, С, POL, CHL, строится модель состояния развития студента [4,5] рис. 6.

B( час/раб)

A (час/раб)

pol2

C (час/раб)

POL (%)

C pol1

chl1

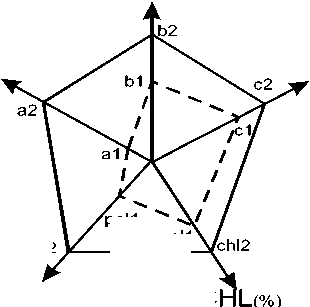
Рис. 7. Модель состояния развития студента

На рис.7 пунктирным контуром a1,b1,c1,pol1,chl1 изображен уровень способностей первого студента, a2,b2,c2,pol2,chl2 – уровень способностей, к которым должен стремиться студент. Если значения параметров окажутся недостаточными, то необходимо вести подготовку по их развитию и росту значений.

Таким образом, по построенной модели выявляются параметры инженера и их значения, которые позволяют определить эффективность результатов его труда.

Каждый студент должен стремиться достичь наивысшего, близкого к идеальному уровню способностей, используя уже имеющиеся способности, и чем выше будут показатели этих параметров, тем успешнее будет решать сложные проблемы будущий инженер.