Особенности обобщения подобных явлений в процессах тепловой обработки рыбы

При разработке приближенных расчетных методик определения кинетики сушки, основанных на общих закономерностях процессов импульс интенсивного развития отражен в работах таких известных ученых прошлого века, как Лыков А.В., Гинзбург А.С. [1,2] и др.

Исследования основывались на использовании теории подобия, где доказывается, что подобные явления характеризуются числами подобия, величина которых характеризует сложившиеся соотношения между взаимодействующими факторами [3]. В теории подобия доказывается, что в подобных явлениях может быть найден определенный набор безразмерных чисел подобия. Каждый процесс характеризуется уравнением подобия, включающим ряд чисел подобия в определенных соотношениях между собой. Такое уравнение представляет собой, по сути, математическую модель процесса.

Из теории сушки известно, что иногда применяются числа подобия, имеющие ту или иную размерность, однако и они могут быть использованы для построения кривых кинетики сушки в обобщенном виде [1,2,3].

Обобщение множества подобных явлений обезвоживания в процессах вяления, холодного, полугорячего, горячего копчения, а также обжаривания рыбы нами предлагается проводить на базе следующих безразмерных чисел подобия [4, 5, 6]:

to to to т т т am am ^k 1 ’ tok 1 tok2 , тk 1 , ткi тк2 , amk 1 amk2 , где тк[- продолжительность обезвоживания от начальной влажности to0 до влажности в юи первой критической точке К на кривой кинетики обезвоживания (рисунок 1); т2 - продолжительность обезвоживания от первой критической точки К1 с влажностью ^i до второй критической точки К2 с влажностью на ^2 кривой кинетики обезвоживания (рисунок 1); a , amkk - коэффициенты потенциалопро-водности влагопереноса в точках К1 и К2 на кривой кинетики обезвоживания; т, to, am -текущие значения продолжительности обезвоживания, влажности, коэффициента потенциа-лопроводности влагопереноса, соответственно. Здесь влажности to, ^i, to2 рассматриваются как количество влаги в рыбе, отнесенное к массе сухого вещества, %.

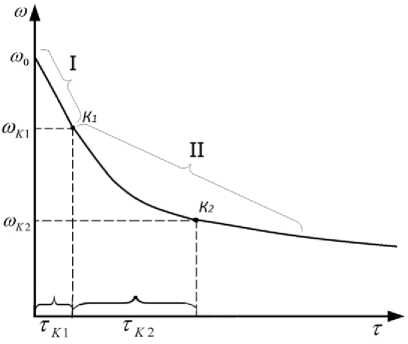
Рисунок 1. Кривая кинетики обезвоживания: I-период постоянной скорости обезвоживания (период разогрева из-за его малости не учтен); II - период падающей скорости обезвоживания

Используя представленные числа подобия, были найдены математические модели кинетики обезвоживания рыбы в указанных выше процессах [6]:

а) для процесса обжаривания:

т = Tk 1

+

1, to , ^T k 1 " ^T k 2 exp 7^{( a} --)

b       ^to k 1

где a и b-коэффициенты (a=0,946, b=0,048 при

обезвоживании в пределах от ю _и, to k ₂; a=0,982,

b=0,098 при обезвоживании в от ^2 до конечной влажности to );

к

б) для процессов вяления и холодного копчения:

т = Tk 1

^T k 2

exp(6,84 - 6,3

to tok 1

to tok 2

0,5

)

в) для процессов полугорячего и горячего

копчения:

^Т = 1^ 1 ^ k 2 exp

3,99 - 3,88( ^toto )^{2 to} k 1 ^to k 2

0,5

I .  (4)

В выражении (2) была использована для

to z т Т . обобщения процесса зависимость---= ^(--), tok 1       Тk 1 Тk 2

^{to to} p / T ^т . а в уравнениях (3) и (4) --- = f (--).

^to k 1 ^to k 2        ^Tk 1 ^Tk 2

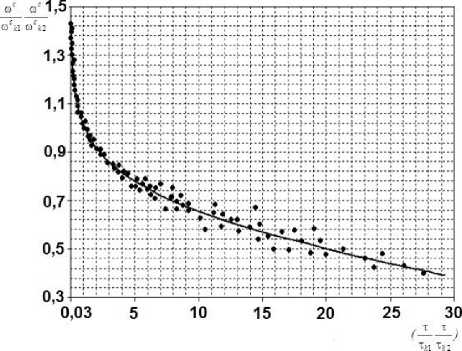
Последняя на примере уравнения (4) приведена на рисунке 2, из которого видно, что экспериментальные точки, полученные при исследовании закономерностей обезвоживания в процессах горячего и полугорячего копчения (сушки), расположены вокруг одной кривой [4]. Критерий Фишера при этом составляет более 2400, значимость числовых

коэффициентов - примерно 100 %, что позволяет утверждать о взаимосвязи данных величин.

^am  ^am = 3,5 ■ 10 ^{- 3}exp(5,73 ^toto ) (6)

^a m_kl ^a m_kl                         ^to k 1 ^to k 2

сс

Рисунок 2. Зависимость сс to k 1 to k 2

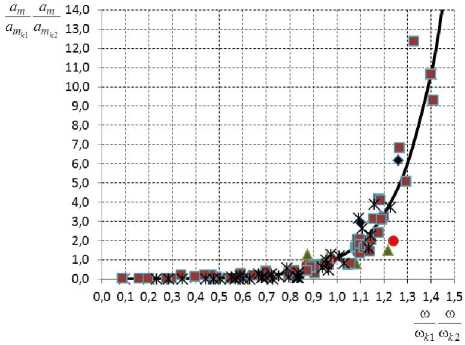
Рисунок 3. Зависимость ^m*__^a™_ = ^ ( —__— )

a a        to  ю^, mk1   mk2           k1 k2

= f(——)

^Т k 1 ^Т k 2

Используя числа подобия

a a tt mm и a mk1   mk2

to to

® k 1 ^to k 2

нами было получено уравнение обобщенной зависимости коэффициентов по-тенциалопроводности массопереноса для про- цессов вяления и холодного копчения:

a

m

0,5

am " am_t2 exP^(6,32 — — - 6^,36) k ¹       k ^{2                to} k 1 ^to k 2             J

.  (5)

Если найти произведение ткх ■ ткг в выражениях (2)-(4) или a ■ a в (5), то пред- ставляется возможным находить конкретные зависимости го = f (т) или am = f (to) в процес- се вяления и холодного копчения.

Представляет интерес, а возможно ли обобщение коэффициентов диффузии влаги в процессах вяления, холодного, полугорячего и горячего копчения, а также обжаривания одной обобщенной зависимо- am  a         го го стью —m--— = ^(--) .

a_m a         to   го_к1

m_{k 1}    m_{k 2}             k 1     k 2

Данная зависимость приведена на рисунке 3. Множество экспериментальных точек, как видно из рисунка, лежит вокруг одной кривой. Критерий Фишера достаточно высок, более 640, что свидетельствует о том, что эти величины взаимосвязаны. Математически кривую, приведенную на рисунке 3, можно выразить следующим уравнением:

Критические влажности to_H и to _{k 2} при обезвоживании рыбы не зависят от режимных параметров, геометрических размеров ее, способа или метода энергоподвода. Они зависят в основном от ее химического состава.

В рыбе из всех химических соединений преобладает вода, поэтому предпочтительно найти изменение критических влажностей от начального содержания влаги to ₀, %. Эта зависимость статистически достоверно выражается следующими выражениями [6]:

to _k 1 = 1 , 069 to 0 ' ⁹⁶⁹ ;                    (7)

to _{k 2} = 0 , 784 to ₀ + 2 .                  (8)

Чтобы найти произведение тк1 ■ тк2 из выражения (2), необходимо сначала найти Tk 1 из выражения:

^to 0 - ^to k 1

Т k 1 = n ’        W здесь N - скорость обезвоживания в первый при тепловой обработке рыбы (период постоянной скорости обезвоживания). Остальные обозна- чения известны.

Для определения скорости обезвоживания N в процессах обжаривания [6] предложено следующее эмпирическое выражение:

N = -36,6 + 0,18to0 + 63,5(— - 0,171) + m          , (10)

+ 0 ,61(Tm - 423)

где to0 - начальная влажность рыбы на сухую массу, %; S / m – удельная поверхность

рыбы, м²/кг; Т м - температура масла при обжаривании, К.

Пределы применения уравнения (10): 230 <© ₀ < 430%;  0 , 12 < S/m < 0 , 234 м²/кг;

403 <  T M <  463 К;

Продолжительность обезвоживания т_кг от с© до ©_кг находим из следующего выражения:

^т к 2 = ^т к 1 exp( 777^7 ^{( 0} . ⁹⁸² -— )) • (И) 0 , 098        ©_и

Для определения произведения т _к 1 • т _{к 2} в выражении (3) необходимо найти влажность рыбы через 24, 48 или 6 часов обезвоживания и подставить эти значения т и ю в уравнение (3).

Значения ю и т находим из уравнений:

ю _{( т} = 24) = ю 1 - 3,024 X р °’²⁵ ( ю ₀ ^о - 50)(10 - - 0,6)^0,5 , 0²⁾ m

Ю ( т = 48) = Ю - 3,792 X р ⁰-²⁵( ю О - 50)(10 - - 0,6)^0,5 , ⁽¹³⁾

1 , 158 X_р^{0, 25} ( © - 50 )

1 -1 , 591 ^— + 0 , 848 (^—))

m     m

ϕ здесь Xp = t( 1 -j^j) - жесткость режима (t - средняя температура, °C и ф - средняя относительная влажность, %, за процесс); S/m -удельная поверхность рыбы, м2/кг; ©0 — начальная влажность рыбы на общую массу, %•

Выражения (12) и (13) справедливы при выполнении следующих условий:

68 <© 0 <  78%; 0 , 11 < S/m <  0 , 23 м²/кг;

5 <  Х_р <  22 •

Область применения уравнения (14) лежит в пределах:

68 <© 0 < 78%; 0 , 23 < S/m <  0 , 73 м²/кг;

5 <  Х _p <  22 •

Определяя продолжительность обезвоживания в процессах полугорячего и горячего копчения [6] из выражения (9), необходимо найти скорость обезвоживания в первый период N = v ( © ₀ ,S/m,X _p ,v) , где © ₀ - начальная влажность рыбы, %; S/m - удельная поверхность рыбы, м²/кг ; Х р - жесткость режима; v - скорость движения сушильного агента, м/с.

Для жирных видов рыб:

N =1,0+0,016(ю ₀ -180)+24,2( S/m -0,185)+

+0,131 ( Х р -30)+0,350( v -2,0).       (15)

Предел применимости уравнения (15):

180 < © ₀ < 300%; 0 , 19 < S/m <  0 , 34 м²/кг;

30 , 25 < Х_р <  52 , 50 ; 2 <  v < 10м/с.

Для тощих видов рыб:

N =2,9+0,016(© 0 -300)+24,2( S/m --0,185)+0,131 ( Х р -30)+0,350( v -2,0)   (16)

Предел применимости (16):

300 <© ₀ <  500%; 0 , 19 < S/m <  0 , 34 м²/кг;

30 , 25 < Х _p <  52 , 50 ; 2 <  v < 10м/с.

Продолжительность обезвоживания т _{к 2} от первой критической точки К 1 до второй критической точки К 2 находим из выражения:

= • ( ^v) ^{к 2} exp[ 3 , 968 - 3 , 883 (ю_к 1 /ю_{к 2} ) ² ]

Подставив т _к 1 и т_к2 в уравнение (4), можно построить конкретную кривую кинетики обезвоживания при полугорячем и горячем копчении рыбы.

Для определения произведения ^amk 1 • ^amki необходимо найти экспериментальным путем одно значение коэффициента по-тенциалопроводности масопереноса a _m при конкретной влажности © и подставить эти значения в уравнение (5) для вяления и холодного копчения или в (6) - для всех рассматриваемых процессов.

Таким образом, уравнения (2)-(6) являются обобщенными выражениями множества зависимостей © = f( т ) и a _m =^ ( © ) •

Физическая сущность процессов обезвоживания состоит в следующем^

На кривых кинетики обезвоживания рыбы имеются критические точки К1 и К2. Критическая точка К1 характеризует завершение удаления влаги, удерживаемой на поверхности рыбы силами поверхностного натяжения, влаги макрокапилляров и осмотически связанною Эти виды влаги имеют наименьшую энергию связи с материалом, поэтому и удаляются в первую очередь. Обычно в капиллярно-пористых коллоидных телах вторая критическая точка возникает при переходе от удаления микрокапиллярной влаги к адсорбционно связанной. Однако адсорбционно связанной влаги в рыбе содержится не более 10 % от общей массы. Конечная же влажность в процессах вяления, холодного, полугорячего, горячего копчения и обжаривания значительно выше. Так почему же при удалении влаги микрокапилляров на кривых кинетики обезвоживания имеет место критическая точка К2, которая характерна для случая перехода от удаления влаги с меньшей энергией связи к удалению таковой с большей энергией связи с материалом? При изучении изменения радиуса микрокапил- ляров в процессе обезвоживания установлено, что радиус капилляров по мере обезвоживания может уменьшаться в 5-7 раз [2, 4, 6]. А чем меньше радиус капилляров, тем выше энергия связи c материалом. Поэтому при достижении в точке К2 критической влажности ω происходит уплотнение продукта и, следовательно, уменьшаются размеры микрокапилляров, особенно в приповерхностных слоях продукта. То есть, в данном случае, тk2 характеризует изменение внутренней структуры материала, его внутренних свойств. Это изменение оказывает влияние на замедление процесса обезвоживания.

Продолжительность обезвоживания т _k 1 до первой критической влажности ω обратно пропорциональна скорости обезвоживания N в период постоянной скорости обезвоживания т_к J = ф ( 1 /N) . В свою очередь, скорость обезвоживания N зависит от химического состава продукта (в данном случае от ω ^о ), геометрических размеров тела и режимных параметров сушильного агента. Следовательно, и продолжительность τ зависит от всех перечисленных выше факторов.

Из изложенного можно сделать следующий вывод: продолжительность обезвоживания τ от начальной влажности ω до первой критической влажности ω характеризует влияние на интенсивность процесса обезвоживания химического состава, геометрических размеров тела и параметров сушильного агента, а продолжительность обезвоживания τ от первой критической влажности ω до второй критической влажности ю _k2 косвенно учитывает влияние на скорость процесса изменение внутренних свойств материала.

Из уравнений (7), (8) очевидно, что критические влажности ω и ω являются функцией начальной влажности ю ₀ , с другой стороны, ю _k 1 и т _k 1 , ю _k2 и т _k2 на кривых кинетики обезвоживания являются координатами критических точек К 1 и К 2 , характеризующих влияние режимных параметров, геометрических размеров тела и химического состава, а также изменения внутренних свойств продукта на скорость обезвоживания.

Таким образом, можно сделать вывод о том, что использование безразмерных чисел подобия на базе (1) в анализе обезвоживания рыбы при ее тепловой обработке позволяет получать достаточно простые математические модели. В сочетании с уравнениями, найденными эмпирическим путем, эти математические модели откры- вают уникальную возможность нахождения кривых кинетики обезвоживания расчетным путем.

В тепловых процессах, таких как обжаривание, полугорячее и горячее копчение [6], важно иметь представление о том, как нагревается продукт, с какой скоростью, каковы расходы тепла на процесс, когда наступает кулинарная готовность.

То есть необходимо знать изменения тем- пературного поля по толщине продукта и как изменяются температуры среднеобъемная и в цен- тре продукта.

Темпы нагрева рыбных продуктов в тепло- вых процессах также зависят от химического со- става, геометрических размеров нагреваемого тела и режимных параметров воздействующей на них греющей среды.

Обычно при тепловой обработке пищевых и рыбных продуктов процессы нагрева и обезво- живания взаимосвязаны и оказывают влияние друг на друга. Поэтому следующие безразмерные числа подобия, вероятно, могут быть применены и при выявлении обобщенных кинетических уравнений нагревания рыбы:

T T. Тц тц . т т. ю ю

T k 1 T k 2    ^T k 1 ^T k 2    ^T k 1 ^T k 2    ^ю k 1 ^ю k 2

здесь T – текущая среднеобъемная температура, К; T ц – температура в центре изделия, К; T k1 , T k2 – среднеобъемные температуры в критических точках К 1 и К 2 кривой обезвоживания, К. Остальные обозначения известны.

Действительно, построив в обобщенных координатах изменение среднеобъемной температуры от степени обезвоживания при обжаривании рыбы и полугорячем копчении ее, все точки статистически достоверно можно отобразить „   ~„ T T    z ю ю одной зависимостью--= v(--), при-

^Tk 1 ^Tk 2       ^ю k 1 ^ю k 2

веденной на рисунке 4.

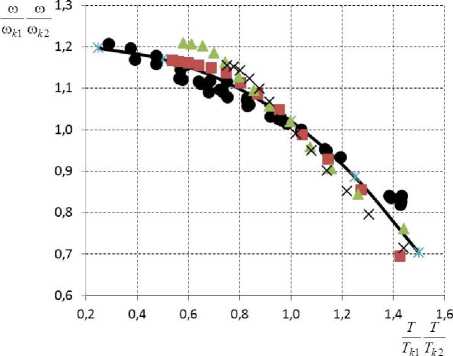
^{T T ю ю} , Рисунок 4. Зависимость-- = v (--)

^Tk 1 ^Tk 2       ^ю k 1 ^ю k 2

На рисунке 5 приведена кривая кинетики нагрева в обобщенных координатах:

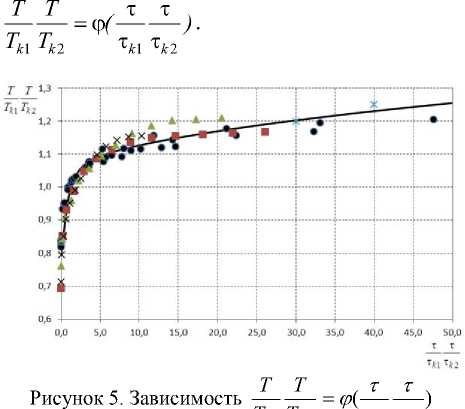
T k 1 T k 2        ^T k 1 ^T k 2

Статистически достоверно, что множество кривых кинетики нагрева разных процессов сведены в одну обобщенную кривую.

Математические модели нагрева рыбы в обобщенном виде представляются достаточно несложными уравнениями:

—— = 1 , 202 - 0 , 181 < —— ) ²⁵

T k 1 T k 2                   ® k 1 ® k 2

;  (17)

—— = 1 , 022 + 0 , 033 (——) °' ⁵

T k 1 T k 2                        ^T k 1 ^T k 2

- 0 ,222exp( - ^T — )

^т k 1 ^т k 2

-

.

Критерий Фишера для уравнения (17) составляет 1059, а для зависимости (18) – 583. То есть имеет место существенная связь между величинами в обоих уравнениях.

Для многих тепловых процессов необходимо знать температуры в центре продукта от продолжительности процесса (обобщенная зависимость приведена на рисунок 6).

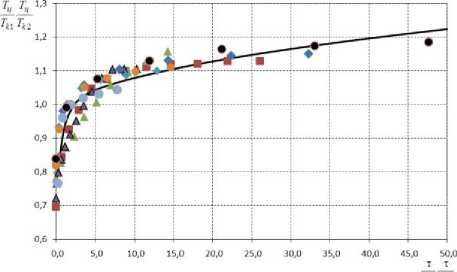
т_и t,₂

Рисунок 6. Изменение безразмерной температуры в центре продукта от продолжительности процесса

Кроме того, зависимость температуры в центре продукта от степени его обезвоживания также можно отобразить одной зависимостью (представлена на рисунок 7).

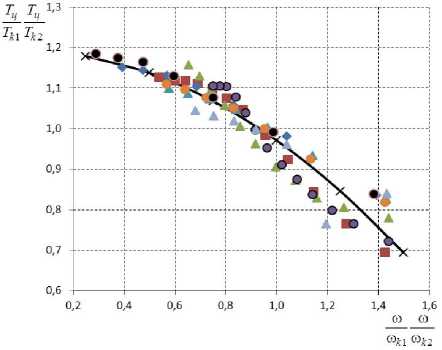
Рисунок 7. Изменение безразмерной температуры в центре продукта от степени обезвоживания

Математическая модель нагрева центральных слоев образцов рыбы в обобщенных координатах, изображенная на рисунок 6, выглядит следующим образом:

T T

— — = 0 ' 962 + 0 , 037 (——) ^{0 , 5} -

^Tk 1 ^Tk 2                      ^T k 1 ^T k 2

- 0 ' 193 exp( -— —)

^T k 1 ^T k 2

Математическая модель зависимости, изображенной на рисунок 7, выглядит следующим образом:

T L T L = 1 ' 193 - 0 , 222 ( ^{H H} ) ² .    (20)

T k 1 ^Tk 2                   ® k 1 ® k 2

Критерии Фишера также достаточно высоки. Для процессов, изображенных на рисунке 6, он составляет более 382, а для множества процессов, которые описываются одним обобщенным уравнением (20), критерий Фишера равен 607.

В представленных выше уравнениях нахождение произведений т _k 1 • т k ₂ и to _k 1 • to _{k 2} уже рассмотрено в данной работе.

Нахождение произведения T_k , • T_k2 нами разобрано в более ранних работах [6]:

T _k 1 = — 0 - 6 1 ( to 0 -to _k 1 ) , (21)

Tk 2 = Tk 1 - b2 ( to k 1 -to k 2 ) , где T0, Tk1, Tk2 – среднеобъемные температуры изделия в начале нагревания и при достижении критических влажностей ω и ω , соответ- ственно, К; to0, tok 1, tok2 - начальная, первая и вторая критические влажности, соответственно, %; b1, b2 - температурные коэффициенты температурной кривой.

Для процессов обжаривания:

b = 0,909 + 0,47(т_к 1 - 1,5) + 0,215( т 1 - 1,5) ^ 1 - 2) , ⁽²²⁾

b2 = 0,59 + 0,1033(тk 1 -1,1),(23)

b3 = 0,578т k1-0,678

Выражения (21)-(24) применимы в пределах от 1,1 мин. <  т_к [ <  2,5 мин.

Для процессов полугорячего копчения:

b1 = 2,58• 0,736к ,(25)

b2 = 1,88• О,740к ,(26)

b3 = 0,095exp(3,447/ т k 1)(27)

Область применения уравнений (25)-(27) лежит в пределах 2,5 мин. <  т_к , <  7,5 мин.