Physical and mathematical model of the processes of a device for processing watermelons
Автор: Nazimbekova A.E., Tlevlessova D.A., Kayrbaeva A.E.
Журнал: Вестник Алматинского технологического университета @vestnik-atu
Рубрика: Технология пищевой и перерабатывающей промышленности
Статья в выпуске: 1 (135), 2022 года.
Бесплатный доступ
The knowledge of the grinding processes of the pulp of fruits and vegetables is not sufficient. In this article, we examined the processes of destruction, grinding, mixing the pulp of watermelon. The criterion equations of these processes are derived taking into account the indicators of the pulp and peel of the watermelon. The derivation of criteria equations for calculating the characteristics of the processes used in the processing of watermelon fruits is considered. The mechanic-technological basis for calculating and designing machines for processing watermelons for food purposes is outlined. The results of experimental studies to determine the optimal kinematic and structural parameters of these machines are presented. The basic physic mechanical and rheological properties of watermelon fruits are given. One of the tasks set for the researcher was to choose a physical model of the processes of separation of pulp from the crust, destruction, grinding of pulp and mixing of the pulp. The values of these quantities depend both on the kinematic parameters of the dynamic interaction and on the physic mechanical and rheological properties of the fruits of melons. The obtained criteria equations can be used to determine the technological parameters of machines where it is necessary to destroy the fetus with minimal energy costs.
Watermelon, criteria equations, process calculation, cutting, piercing, disruption, flesh, pulp
Короткий адрес: https://sciup.org/140293488
IDR: 140293488 | УДК: 62-932.4
Текст научной статьи Physical and mathematical model of the processes of a device for processing watermelons
When analyzing the process of the destruction of the fetus, it is necessary to take into account its physical and mechanical properties, which should be generalized by creating a model of plant material that allows reflecting such fundamental properties of the material as elasticity, viscosity and ductility. The model for gourds is determined by the structure of the fetal cortex, consisting of a solid skeleton and a semiliquid, liquid or gaseous substance filling the gaps between the solid elements of the cortex and the internal cavity of the fetus. Obviously, a more real model should contain a greater number of simple elements, but practice shows that the use of more than three or four elements in models significantly complicates the possibility of visual observation of the behavior of bodies while changing so many of its properties.
Similarity theory allows, without integrating differential equations, to establish a relation- ship between similarity criteria and to formulate a criteria equation that will be valid for all similar processes. Moreover, to derive the criterion equations, it does not need any simplifications that are usually introduced in cases of analytical solutions of differential equations describing a complex phenomenon. Processes of the same physical nature are called similar if their criterion equations completely coincide.
Any of the technologies for processing fruits includes the operation of the destruction of the fetus.
Knowledge of the physical properties of food materials is necessary for the design and optimization of the processing process [1].
While Multipurpose Optimization (MOO) has provided many methods and tools for solving design problems, food processes have gained little benefit from them. MOO covers the definition of performance indicators, process modeling, integra- tion of preferences, evaluating compromises and finding the best compromises [2].
Aremu, A. K., Ogunlade, C. A. studied the yield of juice on three fruits: orange, pineapple and watermelon. In their studies, the fetal juice constant (in decimal form) was also calculated and recorded. Each experiment was repeated three times for peeled and unpeeled pineapple, orange, and watermelon using four sets of sieves. The following indices are described by Oguntuyi (2013), Kasozi and Kasisi-ra (2005), Abulude et al. (2007), Samaila et al. (2008), Aye, and Abugh (2012) were used to calculate juice yield, extraction efficiency and losses during machine extraction, while the juice constant was obtained from the ratio of the sum of the masses of extracted juice and chaff juice to the mass. The fruits fed the mass of juice in Chaff was determined using the ASAE method (1983), applied by Oje (1993), Oyeleke and Ollaniyan (2007), Aviara et al. (2008), Olaniyan (2010), Adebayo et al. (2014), Olaniyan and Obajemihi (2014)a) Juice yield,
Wj-XlOO
JY, % = lOOfWjg,
-
b) Extraction Efficiency, % =
wfs*X
-
c) Extraction Loss %
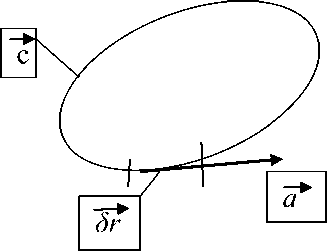
too d) Juice Constant, X = Where: WJE is Mass of juice extracted in grams, WRW is the Mass of residual waste in grams, WFS is the Mass of fed sample in grams, X is the juice constant of fruits in decimal [3]. Methods We studied two varieties of watermelon "Sweet Krimson", zoned in the Turkestan region, and "Dishim." For experiments, together with KazNIIPO Institute for Potato and Melon Growing, 60 pieces were randomly involved. Fruits were taken after checking for defects with a thorough visual inspection, during laboratory tests and studies at 5 ± 1 ° C, 90 ± 5% relative humidity before use. Also, the shape index was used to calibrate the watermelon fruit. The shape index was calculated. During the experiment, a relationship was found between a weighty watermelon and a watermelon shape index. The average weight of wa- termelons was 8 kg, while the circumference of such watermelons was 78 ± 2.1 cm. Mechanical Characteristics Watermelon is also designed to design appropriate machines. For further research, watermelons with the same shape index are discarded. 5 unit of watermelon are made (peel, mechanical armor, pulp parenchyma, etc.). the same size 3cm x 3cm, each experiment was carried out 5 times according to the following methods. 1 .Determination of ultimate shear stress of food products This technique is based on determining the ultimate shear stress in determining the parameters: Fost - residual loading force, g; h - penetration depth, m; 5 is the ultimate shear stress, Pa. The final result can be taken as the arithmetic mean of the values of the results of three determinations: 5 = KconFost / h2, Pa 2 .Method for determining loading force 3 .The study of the strength characteristics of watermelon fruit 4 .Method for determining the strength characteristics on Reotest RN4.0 where: Kcon - coefficient of the cone (1.1 -according to the passport of the device); Fost -the residual loading force on the indenter "cone", N, - is determined according to the schedule as a constant value of the load value stress after relaxation of mechanical stresses; h -penetration depth, m, - corresponds to the value of the steady-state residual loading force. The method is based on determining the parameter of the loading force Fh. The final result was the arithmetic mean of the results of three determinations. Change in loading force on the indenter depending on the depth of its introduction into fresh, frozen and thawed fruits. After uniformly slicing into different parts of the fetus, pieces of the fetus 10 mm thick were placed on the apparatus table close to the indenter, after which the apparatus conducted research and plotted. The experimental research program includes the determination of the strength characteristics of a watermelon and its parts. For research, winter varieties of watermelons with a thick crust and a dark color of the cuticle were taken. To register the data, the ST-2 structuremeter device was used. Raw materials are cut with a thickness of not more than 1 mm, samples are taken from three slices of watermelon, sliced into 2 cm wide slices. From the prepared sliced slices, take the same sections of the slice, parallel to each other. We measure raw materials in shear, plate-plate. We determine the fracture strength, then identically prepare three more samples from the same sections of the segments and conduct oscillation tests. The results of the analyzes are presented in the form of a graph and table. Figure 1 - areas of sampling, watermelon in the context In Figure 1, the region 1 is the core of the In 2005, foreign colleagues from India inves-watermelon, approximately 5 cm in diameter, tigated the fruits of a watermelon with red pulp on the region 2 of the pulp parenchyma is the main an Instron plant manufactured in Great Britain, part where the seeds are located, approximately shown in Figure 2 (Instron, Canton, MA) [4], we 15-20 cm, region 3 is the mechanical armor, the conducted similar studies on a Structometer ST 2 cortical zone, from 23 cm in diameter, then re- and obtained the following data. gion 4 - white peel (epidermis + cuticle) The strength of the crust is determined first with the cuticle, then without the cuticle in different directions. а) б) Figure 2 – Texturometers: а - Instron, Canton, MA, b- Structurometer CT 2 Results and their Discussions Russian scientists Shaprov M.N., Semin D.V. et al. also conducted similar studies, the results of which on the Volga watermelon are given in the sources [5,6]. Also, experiments were conducted according to the methodology of the scien- tific consultant of the Doctor of Technical Sciences, Professor M. Shaprov, who did research on the installation they assembled, we conducted research on the CT 2 structureometer and the following data were obtained, presented in table 1. Our results in table 2 Table 1 - Difference in maximum shear stress depending on the cut-off area of the watermelon Watermelon area Maximum Shear Strength (N) Maximum shear stress (N/мм2) Range 1 4±0,2 0,048±0,009 Range 2 5,5±0,1 0,069±0,002 Range 3 10±0,2 0,0139±0,003 Range 4 50±0,2 0,070±0,007 Table 2 - Strength characteristics of watermelon Region Fracture force, N Puncture Force, N Hardness, kg / mm2 Cutting force with a flat knife N / cm along across Watermelon bark Stalk of watermelon 470,4±2,7 131,0±1,5 0,91±0,1 28,5±0,3 36,9±0,62 Watermelon equator 432,5±6,8 109,1±0,72 36,9±0,4 37,1±0,5 receptacle 440,9±5,3 106,8±2 26,8±0,52 39,5±0,5 Watermelon pulp peduncle 176,9±2,7 13,0±0,2 10,6±0,15 equator 102,8±0,73 12,6±0,15 12,1±0,13 receptacle 166,4±2,7 9,33±0,14 8,6±0,14 The obtained research data was used to calculate and design a device for cleaning a watermelon from a cuticle, chopping and extracting pulp, and slicing a peeled peel into even cubes for making candied fruit. The elastic modulus of watermelon amounted to 9.79 ± 0.94 × 100 Pa and vertical compression to 8.92 ± 0.78 × 100 Pa under vertical compression. The efficiency of juice extraction and losses are calculated by the following formulas: а) Juice yield, JY, % = =31,6±0,23 b) Extraction Efficiency, % = wfs«X =38,3±1,4 c) Extraction Loss % = =6,4±1,2 Separation of pulp from the peel The separation of pulp from the walls of the peel occurs by sliding cutting of the pulp from the inner walls of the peel Elementary energy (work) dA (Дж), put it: dA = dA1 + dA2 + dA3 Where dA1 is the elementary work spent on volumetric plastic deformation, J. dA2 - elementary work spent on the formation of an element of a new surface (at the limit of molecular forces or surface energy), J; dA3 — elementary energy spent on compensation for losses associated with the friction process and heat generation, respectively, J. dА where НF is a constant for a given material, characterizing its surface-active properties or otherwise specific work (energy) spent on the (1.1) The terms dA1, dA3 are negligible in comparison with the value of dA2 We take into account only the value dA2 for cutting with sharp edges of the blades: = HF • 2dF (1.2) formation of a unit area of the material being cut, J / m2; А = 2H ∫ dF (1.3) dF - elementary cut surface area, m2 (1.4) = p F⋅dτ Where dТ is the elemental cutting force when separating the pulp from the inner surface of the watermelon; vр - cutting process speed; Fр - cutting area. The mathematical model of the process of cutting the flesh is presented in the form of a system of equations: or otherwise: (1.5) (1.6) Grinding pulp inside the cavity Grinding occurs in the cavity of a watermelon, after the introduction of a working organ. The fragile structure of the pulp of watermelon is destroyed. Destruction occurs as a result of compression deformations (mainly) and cutting. Arguing in a similar way to (1.1), we obtain: dA = dA1 + dA2 + dA3 We neglect only the value dA3 dA = dA1 + dA2 The elementary work dA1 spent on volumetric deformation is expressed by: dА σ2⋅ dV 2E (1.7) Where σ – fracture stress with pressure blades, Pa; dV – elementary volume increment during deformation, м3; Е – the elastic modulus of the second kind, characterize the strength properties of this material (pulp of the product), Pa. Total energy (work) spent on volumetric deformation: We neglect only dA3 dA = dA1 + dA2 Total energy (work) spent on cutting: А = 2 H ∫ dF The speed of the process is determined by the combined effect of crushing and cutting strains: dR vp= (1.8) F ⋅ dτ Where dR = dR1 + dR2 is the elementary crushing and cutting force; F is the processing area. The mathematical model of the process of destruction of the pulp will be present in the form of a system of equations: (1.9) or otherwise: /Ж F-dr (1.10) cy'dV dA =----- 1 IE Mixing pulp inside the cavity The process of mixing the liquid is characterized by a complex distribution of velocities in its volume, which depends on the shape, size of the tank and mixer, as well as on the speed of rotation of the mixer blades. According to the Stokes theorem, in a closed loop (with stirring Fig. 3), the circulation of the vector rc =f а • sr (i.ii) с Figure 3- closed loop mixing circuit Where, с - closed loop; а - circulation vector (peripheral speed); Гс- circulation vector а по with closd loop with ( in a particular case around the circumference with stirring);δr - elementary movement (elementary path) In this case, the work (Ac) of the closed-loop motion force expressed: Ас =| R • Sr (1.12) с R - force overcoming resistance of fluid layers, Н. For a unit of time, closed-loop operation is the power expended in mixing in an unsteady mode. dA (1.13) N= cτ According to the first Helmholtz theorem, the angular velocity vector is determined by: 9 = — • rotV (1-14) rotV - circumferential speed rotor, characterizing the intensity of the circular motion and equal to twice the angular velocity: rotV = Q Q = rotV? = 2 • (9 The rotor is the spatial derivative of the velocity, or else the rotor is a vortex equal to twice the angular velocity. If the circulation Tc> 0, then this means that there is a vorticity in the fluid. Thus, mixing of the individual fluid layers and the whole as a whole occurs. When mixing the liquid, the kinetic energy E in J is reported: dE=ρ⋅(ω0⋅x)2 where dЕ is the elementary kinetic energy communicated to the mixer blades; ρ is the density of the liquid system, kg / m3; ω0 is the constant angular velocity of rotation of the mixer, s-1; ⋅ h ⋅ω ⋅ xdx ⋅ (1.15) x - distance from the axis of rotation (rotor axis), m; h is the height of the blade, m; dх - elementary blade length, m; ρ⋅ω03⋅h 2 r2 ∫ x 3 ⋅ dx = r1 ⋅ ρ⋅ω03⋅h⋅(r14-r24) (1.16) Where r1 is the radius of the inner edge of the blades, m; r2 is the radius of the outer edge of the blades, m The elementary friction force (dP) acting on the blade is expressed according to Newton’s law: dP=ξ⋅ρ⋅(ω⋅r0)2dF (1.17) Total force (P) of friction N (hydrodynamic resistance) is determined by: р_ £ • F • р^Ю-ro )2 (1.18) F - blade area, m2. ξ is the drag coefficient of the blade, depending on its shape and the mode of fluid movement. r0 is the radius of the blades, m ω - working angular speed of rotation of the mixer, c-1 Moment of friction Мf: М = §■ F•р-го2• r' (1.19) f8 Operating Torque Мк М = ^рго2•(r,4-r1) (1.20) к8 Where μ is the dynamic coefficient of viscosity of the liquid system, Pa · s Working power (N in W) on the shaft of the mixer is determined: N = М -го к N = hР'го3 •(r,4 - гі4) At a rotational speed of the agitator blades n in rev / s, the angular velocity ω = 2πn and r = d / 2. d is the diameter of the mixer blades. Criteria equation for the pulp mixing process. (1.21) This equation is well known and is used to calculate the working power of the mixing process. N = KN р-и3-d5 (1.22) N is the working power spent on the mixing process, W; KN - power criterion or otherwise modified Euler criterion for mixers; ρ is the density of the liquid system, kg / m3; d is the diameter of the stirrer blades, m; n is the frequency of rotation of the blades of the mixer, c-1. The criteria equation presented in several forms: —= С' Re м k Р •n d Where N р-n3•d5 = Еи« м N = Еимр>- n3-d5 The quality of mixing affected by a correctly selected and calculated angular velocity ω (c-1). It is associated with the so-called relative mixing speed. The final information on the calculations is summarized in table 3. Table 3- Calculation results significative Meaning N,W Total power on the agitator shaft 722 N,W Starting power taking into account overcoming inertial forces 794,2 Мкр, N·m Torque for the selection of the stirrer electric drive 46,7 Р1рез, N Total cutting force including frictional forces 29,4 N1, W Cutting power of the pulp from the bark 230,8 N2, W Pulp cutting power 94,2 n, s-1 Optimum speed 25 ReM Modified Reynolds criterion (for mixing) 129274 N3, W Working power on the agitator shaft 397 Jp Cutting intensity criterion 0,4 .10-3 σ, N / mm Crumple stress 0,17 RD Criterion for the intensity of the action of the shear deformation force 0,11.10-4 V, kg / s Installation performance 8,4 Criterion equations are derived that help to calculate complex processes in the processing of watermelon fruits. Processing difficulties are related to the purpose of the study. The aim of the study is to develop equipment for obtaining a homogeneous watermelon pulp and obtaining a cleaned and undamaged watermelon rind. The peel is processed into candied fruits, and the homogeneous pulp is processed into other types of sweet products. The difficulty lies in the fact that the process of grinding and mixing takes place in the cavity of the watermelon. Conclusions The knowledge of the grinding processes of the pulp of fruits and vegetables is not sufficient. Such aspects as loss of food product quality during prolonged exposure, when cutting the quality of sliced slices, chemical properties of the product, etc. are not taken into account. In this case, we examined the processes of pulp destruction, pulp grinding, pulp mixing, and the exposure time was minimal. The criterion equations of these processes are derived taking into account the indicators of the pulp and peel of the watermelon. One of the tasks set for the researcher was to choose a physical model of the processes of separation of pulp from the crust, destruction, grinding of pulp and mixing of the pulp. The article presents our proposed models, which allow us to calculate the effective dimensions of the working body with a minimum exposure time to the pulp, taking into account the density of raw materials. The values of these quantities depend both on the kinematic parameters of the dynamic interaction and on the physic mechanical and rheological properties of the fruits of melons. A formula for calculating the effective speed of mixing the pulp taking into account the reduction of energy consumption They are described by specific criteria equations obtained on the basis of the similarity theory using the dimensional analysis method. The derived equations are new and are specific to this device. In the above equations, the obtained characteristics of the pulp are used (density, breaking force, etc.) The obtained criterion equations can be used to determine the technological parameters of machines where it is necessary to destroy the fetus with minimal energy costs.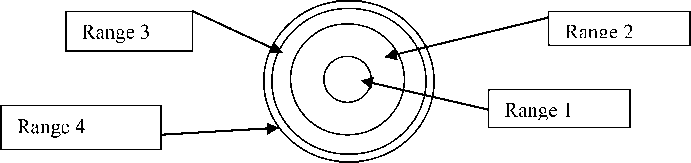

dF - elementary surface increment during
Total energy (work) spent on cutting:
cutting deformation, m2.
F is the internal surface area of the slice, m2.
2F - the newly formed surface is equal to the double sectional area of the section, m2.
With a constant with a known configuration of the cutting area, the work will be expressed:
А =2НF ·F
The speed of the cutting process, as the most important kinetic factor is expressed:
dТ
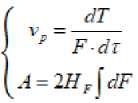
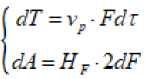
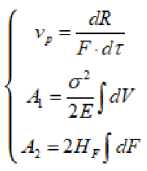
Список литературы Physical and mathematical model of the processes of a device for processing watermelons
- Henrique C. B. Costa, Danylo O. Silva, Luiz Gustavo M. Vieira, Physical properties of açaiberry pulp and kinetics study of its anthocyanin thermal degradation, Journal of Food Engineering, Volume 239, 2018, PР 104-113.
- Martial Madoumier, Gilles Trystram, Pat-rick Sébastian, Antoine Collignan, Towards a holistic approach for multi-objective optimization of food processes: A critical review, Trends in Food Science & Technology, Volume 86,2019, PР. 1-15.
- EDN: WYUWGS
- Aremu, A. K., Ogunlade, C. A. Development and Evaluation of a Multipurpose Juice Extractor. N Y Sci J 2016; 9 (6): 7-14].
- Shrinivas Deshpandu, thesis. http://krishikosh.egranth.ac.in/handle/1/5810028016.
- M.N. Shaprov, D.V. Semin, M.A. Sadovnikov, A.V. Kuznetsov Determination of strength characteristics of fruits of melons and gourds // Bulletin of the Lower Volga Agro-University Complex.-№4 (24), 2011.
- Semin. D.V. The state and level of mechanization in the processing of gourds/ D.V. Semin // Materials of the IX regional conference of young researchers of the Volgograd region.-Volgograd: Volgograd State Agricultural Academy, 2015.-122p.


