Потенциальная деформация упругого параллелепипеда

Математическая модель деформаций

Будем рассматривать несжимаемую среду:

r d u   d v   d w_

div (v )=    +—+= d x   dy

Здесь r ^ ( u , v , w ) - вектор перемещений точек среды.

Введем в рассмотрение потенциал перемещений Φ: r = grad Ф .

Подставляя (2) в (1), получим v 2ф = о,                                             (3)

где V ² - оператор Лапласа.

По теореме разложения Геймгольца, всякую деформацию можно представить как сумму объемной деформации, определяемой потенциалом перемещений Ф, и деформации сдвига, определяемой вектором £ = ( ^ , П , ^ ) ^:

£ = rotv r .                                            (4)

Задачи на определение деформаций сдвига решаются с помощью нахождения компонент рассматриваемого вектора, каждая из которых удовлетворяет уравнению Лапласа. Кроме этого, по аналогии с задачами динамики жидкости, потребуется ввести в рассмотрение аналог функции тока или векторного потенциала, компоненты которого будут удовлетворять уравнениям Пуассона. После решения вопроса с граничными условиями для упомянутых функций можно найти сдвиговые деформации, например, в задачах кручения или комплексных задачах на сжатие и сдвиг, и далее, используя принцип суперпозиции решения (утверждение, обратное теореме Геймгольца), найти решение полной задачи.

В линейной теории упругости задача определения объемных деформаций может быть отделена от задачи расчета деформаций сдвига, что и сделано в настоящей работе. Поэтому ниже будет рассмотрена задача, связанная с нахождением потенциала перемещений Ф.

Обобщенный закон Гука

Предположим, что потенциал перемещений найден. Тогда, используя соотношение (2), можно найти вектор перемещений V, то есть все его компоненты u, v, w.

В механике известны соотношения Коши [1, 3], которые определяют компоненты тензора деформаций через перемещения:

е

д и е = ----, е

"    д x , yy

1 ( д и

д v

xy

+7^

2 у д у д x ^

д v          д w

, е - = д у          д z

• 1    ( д и д w А 1 ( д v д w е = I1I , е =             1

• 2    У д z д x J ^у 2 У д z д у _v

Теперь можно записать реологический закон, связывающий компоненты тензора напряжений с компонентами тензора деформаций. Простейшая линейная форма такой связи носит название обобщенного закона Гука [2]:

Су = ^и^е kk + ² ^ ^е у . ⁽⁷⁾

Здесь по повторяющемуся индексу проводится суммирование. При этом

Х = ----- V E ----•

( 1 + v )( 1 -2v )

E

^ = ---- г 2 ( 1 + v )

- коэффициенты Ляме, E - модуль Юнга,

v - коэффициент Пуассона. Из последнего соотношения для компонент тензора напряжений получаем

^хх = (X + 2o)s+Х(еyy + Еzz),(8)

оyy = (х + 2ц)еyy + Х(ехх + Szz ), azz =(Х + 2ц)£zz +Х(ехх +еyy), а ху = 2 OS ху , a хх = 2 OS хх , a yz = 2 OS yz "

Граничные условия на свободной поверхности

Рассмотрим, например, грани параллелепипеда, перпендикулярные оси 0 х . Здесь, если поверхность свободна, должно выполняться физическое условие равенства нулю нормальных напряжений:

о хх = 0.                                                 (12)

С учетом связи закона Гука это соотношение можно переписать в виде э \ ди , ( Vv дw ) „

(X + 2o) ---+ X —+---1 = 0                           ⁽¹³⁾

7 д х ( д y д z J или через потенциал перемещений где

д2 Ф д х2

+ к

д ² Ф д ² Ф

2+ д y      д z2

= 0

X

( X + 2o )

v

.

1 -v

Аналогично на гранях, перпендикулярных оси 0 y , имеем:

д ² Ф д у ²

+

к

д2 Ф д х2

д ² Ф ' д z ² у

= 0 .

Разностная схема

Решение задачи расчета Ф будем строить итерационно-разностным методом, то есть с использованием простейших симметричных аппроксимаций для вторых производных и метода простой итерации для перерасчета значений искомой величины в узлах разностной сетки. Аппроксимируя вторые производные, входящие в оператор Лапласа симметричными разностями, получим следующий разностный аналог уравнения (3):

a e ^Ф 1 k ⁺ a w Ф +v , k ⁺ a s ^Ф / , _У - 1, k ⁺ a n ^Ф _{м +} 1, к ⁺

⁺ a b ^Ф / , j , к - 1 ⁺ a t ^Ф / , j , к + 1 - a p ^Ф / , j , к = ⁰

Выражая из последнего соотношения Ф ,, , _к , получим рекуррентную формулу для пересчета значений искомой величины во внутренних точках области:

,     = a ^Ф i - 1, j , к ⁺ a w ^Ф i + 1, j , к ⁺ a s ^Ф i , j - 1, к ⁺ a n ^Ф i , j + 1, к ⁺ a b ^Ф i , j , к - 1 ⁺ a t ^Ф i , j , к + 1    (17)

Ф

‘ , ^j , ^к                                                                   a_p                                                              '

Здесь

_ _ 1                1       _ _ 1

a e    a w   A x² ’ a s = a n = "m? ’ a b = a t \z "

Разностная аппроксимация условий на свободной поверхности

Возьмем для определенности левую грань параллелепипеда (перпендикулярную оси 0x). Пусть значение первого индекса, равное единице, отвечает рассматриваемой границе. Введем в рассмотрение фиктивный слой точек, которому отвечает индекс ноль, и положим значение потенциала перемещений в этом слое, охватывающем свободную поверхность, равным нулю. Тогда, используя симметричные аппроксимации всех вторых производных, входящих в (14), можем записать

Ф 2jк . К Ф 1J+Vк + Ф U-Vк

, ^ф _u, к ₊ 1 ^{+ ф} 1,j,к - 1 A z ²

2 k

Az?

J .(19)

A x2      I       A y2

• 1,    j , k =                         2 2k

—т + T +

A x2   A y

В предельном случае к = 0 последнее условие переходит в соотношение ф ю. к

^Ф 2j к

2     ’

являющееся разностной реализацией равенства нулю второй производной от потенциала перемещений по нормальной к свободной поверхности координате в случае, когда в фиктивном слое принимается нулевое значение потенциала. Таким образом, в предельном случае значение потенциала перемещений на свободной поверхности равно половине значения этой величины в ближайшем сеточном узле.

На нижней и верхней гранях параллелепипеда на площадках, перпендикулярных оси, по которой производится сжатие параллелепипеда, задаются следующие дифференциальные условия

дФ_ о, d z

.

5Ф

-   _ w о о z

Разностный вид этих соотношений получается заменой первых производных от потенциала перемещений односторонними разностями, имеющими порядок аппроксимации выше второго.

Результаты расчетов

Ниже в качестве примера применения описанной схемы расчета представлены результаты сжатия упругого куба с ребром 0,2 м. Предполагалось, что это металлический объект, характеризующийся коэффициентом Пуассона v = 0,3. Деформации металлических образцов, происходящие в упругом режиме, составляют всего доли процентов от линейных размеров объекта. Заметим, что математическая постановка задачи допускает использование линейных размеров объекта в системе СИ, то есть в метрах, а расчет перемещения - в технических единицах, то есть в микронах.

На рис. 1 показано распределение нормальной по отношению к боковой границе куба компоненты перемещения в результате его сжатия по вертикали на один микрон. Ввиду симметрии задачи эту же картину имеем на трех других боковых гранях куба. Представленная картина показывает, что вертикальные ребра являются для задачи сжатия по вертикали ребрами жесткости, поскольку наибольшие деформации реализуются в центральной части грани, и наименьшие - у указанных ребер. Кроме того, деформации неравномерно распределены по направлению сжатия, так как максимальные деформации отмечаются в окрестности контакта образца со сжимающим телом.

На рис. 2 показано распределение вертикальной компоненты перемещений ( w -компоненты) в горизонтальном сечении, проходящем через середину куба. Здесь также наблюдаем выраженную неоднородность смещений.

Наконец, рис. 3 представляет горизонтальную составляющую смещения, находящуюся на боковой грани куба ( v -компоненту смещения).

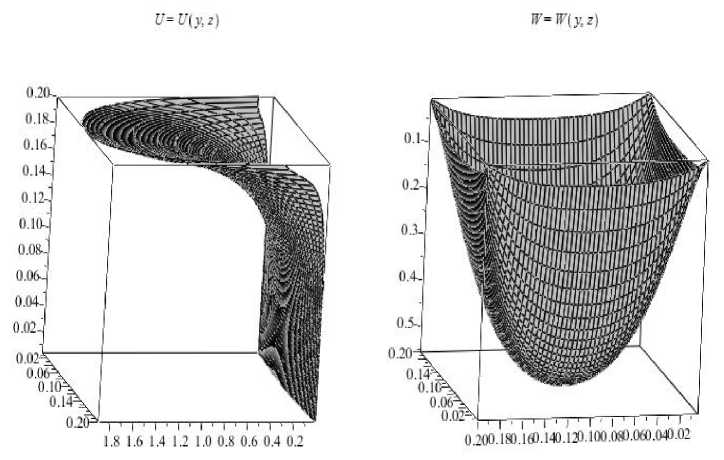
Рис. 2. Распределение продольной по отношению к оси сжатия компоненты перемещения

Рис. 1. Распределение нормальной по отношению к боковой поверхности компоненты перемещения

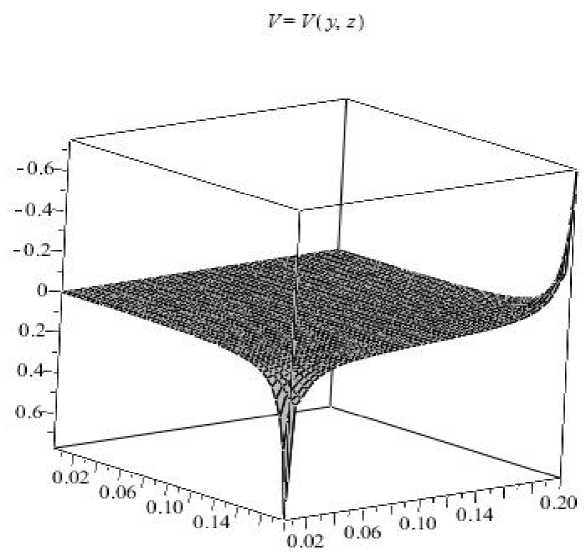
Рис. 3. Распределение горизонтальной и касательной по отношению к боковой поверхности компоненты перемещения

Заключение

В работе предложена схема расчета потенциальных деформаций упругих тел, основанная на введении потенциала перемещений.

Предложена итерационно-разностная вычислительная технология реализации поставленной задачи, главными особенностями которой является простота и универсальность. Рассмотрен пример задачи о сжатии упругого куба, расчетами найдено поле векторов перемещений частиц среды рассматриваемого тела.