Прикладные аспекты оценки бизнеса в процессе трансформации собственности (на примере малых предприятий сферы услуг)

Российский рынок слияний и поглощений характеризуется практически полным отсутствием статистики по сделкам с малыми предприятиями. Все открытая информация о трансформации собственности малых предприятий сводится к цене продаваемого разнопрофильного бизнеса.

С большой вероятностью можно отметить, что активность сделок по слияниям и поглощениям в малом бизнесе высока, но оценить масштабы этого рынка не представляется возможным в связи с отсутствием статистики о закрытых сделках.

В настоящей работе мы представляем разработанную методику оценки малых предприятий. Для репрезентативности методики нами было проанализировано более 200 предложений о продажах предприятий ма- лого бизнеса и рассчитаны мутильпликаторы стои-мости[1].

Нужно отметить, что подобные мутильпликаторы стоимости давно существуют за рубежом. Опыт западных оценочных фирм свидетельствует [2]:

• •    бухгалтерские фирмы и рекламные агентства продаются, соответственно, за 0,5 и 0,7 годовой выручки;

• •    рестораны и туристические агентства – за 0,25-0,5 и 0,04-0,1 валовой годовой выручки;

• •    автозаправочные станции – за 1,2-2,0 месячной выручки;

• •    предприятия розничной торговли – за 0,75-1,5 суммы (чистый доход + оборудование + запасы) и т.д.

Учитывая, что в России подобных мутильпликато- ров стоимости нет, мы разработали собственную методику оценки малых предприятий, которая основана на применении регрессионно-корреляционного анализа. В ходе нашего исследования было обработано более 1000 предложений о продаже малых предприятий. В связи с тем, что не все предложения отражали цену продажи, финансовые показатели, размер продаваемого пакета (доли участия), в выборку вошла только 201 позиция. Нужно отметить, что предприятия, вошедшие в выборку, прошли обязательную предпродажную подготовку, которая включала:

• •    юридическую экспертизу гражданско-правовой документации, относящейся к продаваемому бизнесу;

• •    экспресс-анализ финансового состояния компании;

• •    определение цены бизнеса;

• •    исследование рынка, на котором функционирует объект;

• •    разработку стратегий продажи бизнеса.

Таким образом, методика оценки малых предпри- ятий основана на официально подтвержденных финансовых показателях, что, наряду с фактическим объемом выборки, повышает ее значимость.

Напомним, что для построения надежной эконометрической модели оценки рекомендуется использовать объем выборки рыночных данных, равный 5-7 -кратному числу используемых моделью независимых факторных переменных (ценообразующих факторов), а также то, что одним из используемых показателей адекватности уравнения регрессии является коэффициент детерминации, нижней границей значений которого при решении задачи индивидуальной оценки может быть принята величина, равная 0,75 [3].

Описание методики

Разработанная нами методика оценки малых предприятий основана на применении корреляционно-регрессионного анализа.

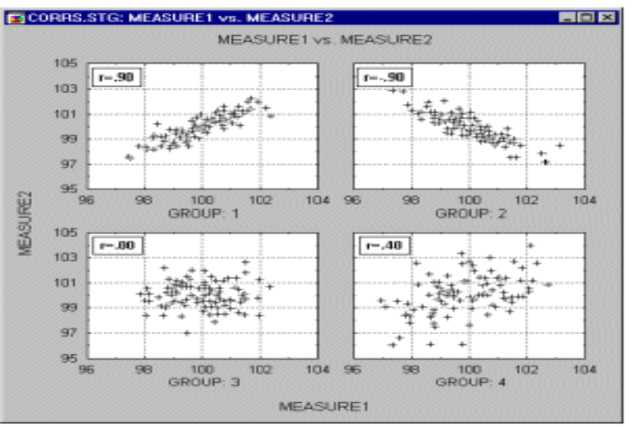
Рис. 1. Примеры выборки

Корреляция представляет собой меру зависимости переменных. Наиболее известной является корреляция Пирсона (r). При ее вычислении предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Значение 0.00 означает отсутствие корреляции [3].

Корреляция Пирсона определяет степень, с которой значения двух переменных «пропорциональны» друг другу. Корреляция высокая, если на графике зави- симость выражается прямой линией, с положительным или отрицательным углом наклона.

Полученная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной.

Напомним, что коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то получится коэффициент детерминации (r2), который представляет долю вариации, общую для двух переменных (иными словами, «степень» зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как «величину» кор- реляции, так и ее значимость.

Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. В свою очередь, значимость определенного коэффициента корреляции зависит от объема выборки. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной y является нормальным (с постоянной дисперсией для всех значений независимой переменной x). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие.

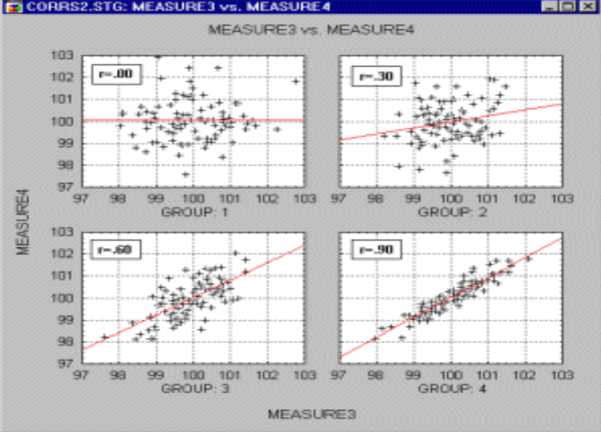
Рис. 2. Примеры корреляции выборки

Корреляция представляет собой меру зависимости переменных. Наиболее известной является корреляция Пирсона (r). При ее вычислении предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Значение 0.00 означает отсутствие корреляции [3].

Корреляция Пирсона определяет степень, с которой значения двух переменных «пропорциональны» друг другу. Корреляция высокая, если на графике зависимость выражается прямой линией, с положительным или отрицательным углом наклона.

Полученная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной.

Напомним, что коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то получится коэффициент детерминации (r2), который пред- ставляет долю вариации, общую для двух переменных (иными словами, «степень» зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как «величину» корреляции, так и ее значимость.

Расчетная часть методики

В качестве переменных при расчете первого му-тильпликатора будут выступать отношение цены предприятия к годовой чистой прибыли (P/E), при расчете второго – отношение цены предприятия к годовому значению объема продаж (P/S).

Расчет мутильпликатора стоимости «P/E» начинается с определения тренда, наилучшим образом аппроксимирующего фактические данные.

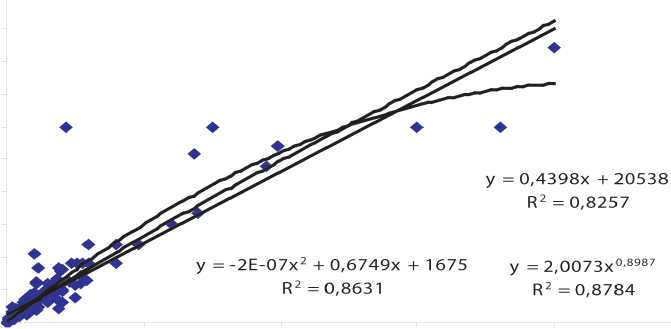
Как показывает график 1, степенной тренд аппроксимирует фактические данные выборки гораздо лучше, чем остальные. Коэффициент детерминации степенного тренда равен 0.8784. Применение других видов тренда (линейного, экспоненциального, логарифмического, полиномиального) не дает такого эффективного результата. Они по сравнению со степенным трендом менее эффективно аппроксимируют значения, коэффициенты их детерминации составляют:

• •    полиномиального – 0.8631

• •    линейного – 0.8257

• •    экспоненциального – 0.4369

• •    логарифмического – 0.5512

1 000 000

900 000

800 000

700 000 с;

5   600 000

S   500 000

га    400 000

300 000

200 000

100 000

500 000      1 000 000    1 500 000     2 000 000     2 500 000

Цена предприятия^

График 1. Распределение линейных связей между переменными выборки и определение тренда, наилучшим образом аппроксимирующего выборку

Учитывая большое количество «выбросов» выбо-рки,1 мы для репрезентативности результатов расчета ограничили переменную «цена предприятия» значени- ем $1,0 млн., а переменную «годовая чистая прибыль» – значением $500 тыс. На графике 2 представлена полученная зависимость переменных.

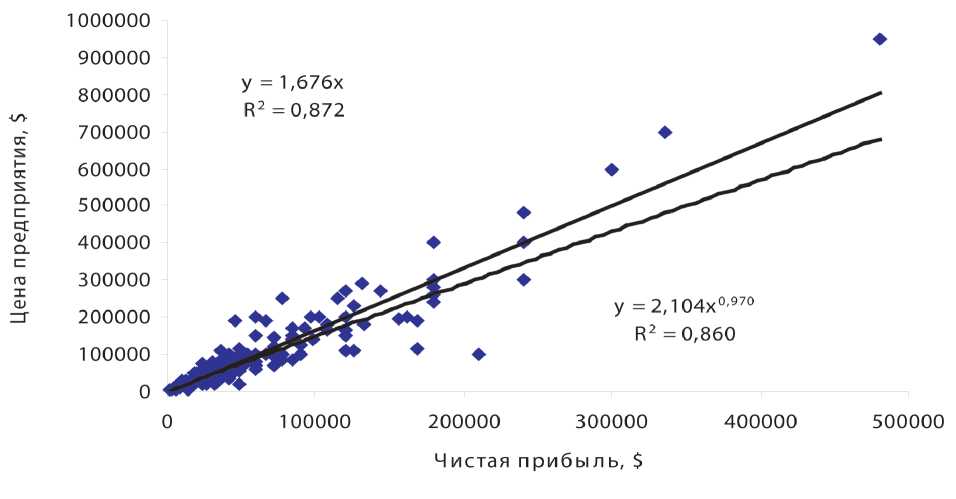
График 2 Распределение линейных связей между переменными (при ограниченных значениях переменных)

По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.

Как показывает график, линейный тренд аппроксимирует фактические данные выборки гораздо лучше, чем остальные. Коэффициент детерминации линейного тренда равен 0.872. Применение других видов тренда не дает такого эффективного результата. Уравнение регрессии, которое должно далее быть использовано для расчета цены предприятия, имеет следующий вид:

у = 1,676*х;

где y- цена предприятия;

х-чистая прибыль предприятия (годовое значение).

Далее мы приводим расчет второго мутильпликато-ра – отношение цены предприятия к годовому значению объема продаж (P/S).

Расчет мутильпликаторов стоимости начинается с определения тренда, наилучшим образом аппроксимирующего фактические данные. Затем на основании уравнения регрессии мы рассчитаем значение мутиль-пликатора стоимости.

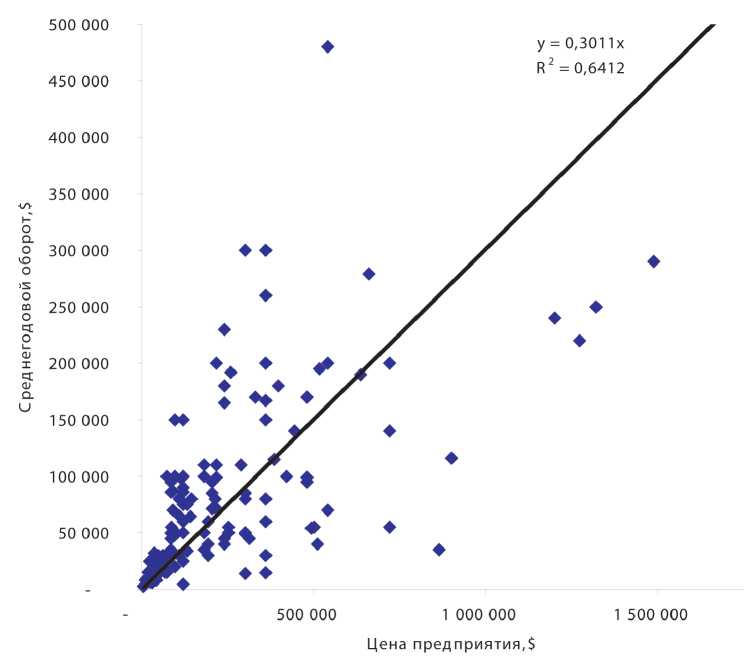
График 3. Определение тренда, аппроксимирующего выборку

Как показывает график 3, линейный тренд не достаточно эффективно аппроксимирует значения выборки. Коэффициент детерминации составляет 0.6412, что ниже критического значения. Применение других видов тренда дает худшие по сравнению с линейным трендом результаты.

Учитывая большое количество «выбросов», мы для репрезентативности результатов расчета ограничили выборку. В качестве ограничения, использовали двукратное отклонение медианного значения отношения «цены предприятия к выручке»:

• •    диапазон разбросов в выборке - 0,04-1,56:

• •    значение медианны целой выборки - 0,42;

• •    двукратное ограничение значения медианы: 0,42/2–0,42*2 = 0,2-0,8.

Как показывает график 4, после удаления «выбросов» линейный тренд аппроксимирует фактические данные выборки гораздо лучше, чем ранее. Коэффициент детерминации линейного тренда равен 0.9471. Применение других видов тренда не дает такого эффективного результата. Уравнение регрессии, которое должно далее быть использовано для расчета цены предприятия имеет следующий вид:

у = 0,447*х,

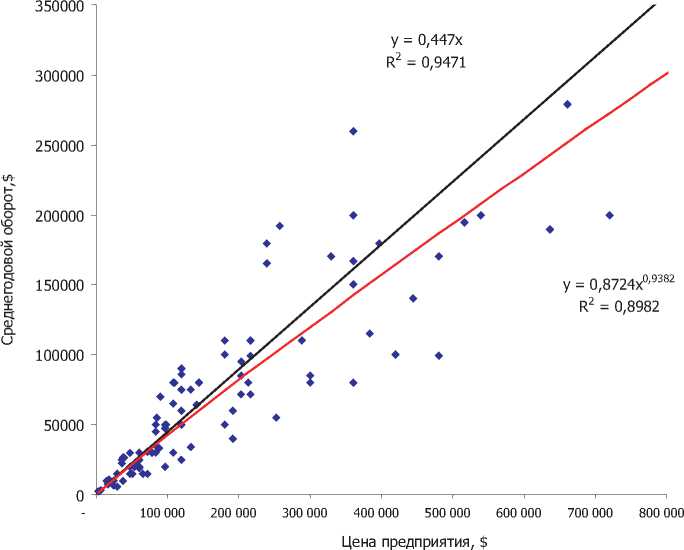
График 4. Распределение линейных связей между переменными (при ограниченном значении медианы)

где y- цена предприятия; х-среднегодовой оборот (годовое значение выручки).

Рассчитанные нами мутильпликаторы стоимости применимы для всего круга разнопрофильных малых предприятий. Дополнительно, в контексте настоящей работы мы рассчитали аналогичные показатели стоимости с разбивкой на предприятия сферы услуг. Результаты представлены в следующей таблице:

Таблица 1

Профиль малого предприятия	Количество сделок	Коэффициент детерминации при расчете P/E	P/E	Коэффициент детерминации при расчете P/S	P/S
Автосервис	11	0,92	1,62	< 0,75	-
Ателье	6	< 0,75	-	< 0,75	-
Видеосалон	5	0,99	1,43	0,99	0,70
Интернет-магазин	7	< 0,75	-	< 0,75	-
Компьютерный клуб	5	< 0,75	-	0,97	0,75
Магазин	29	0,76	1,70	< 0,75	-
Медицинский центр	4	0,97	2,13	< 0,75	-
Парикмахерская	4	< 0,75	-	< 0,75	-
Производство продуктов питания	13	0,84	2,23	0,75	0,36

Мутильпликаторы стоимости

СОЦИАЛЬНЫЕ ПРОЦЕССЫ

Производство ТНП	16	0,94	2,30	0,93	0,39
Ресторан/бар/кафе	13	0,99	1,86	0,97	0,45
Салон красоты	10	< 0,75	-	0,92	0,59
Салон сотовой связи	4	< 0,75	-	0,99	0,20
Стоматологическая клиника	3	< 0,75	-	< 0,75	-
Туристическое агентство	6	< 0,75	-	< 0,75	-
Фитнес-клуб	7	< 0,75	-	0,85	0,50
Фотосалон	4	0,99	1,15	< 0,75	-
В целом по малым предприятиям		0,87	1,676	0,95	0,447

В качестве заключения мы отмечаем, что рассчи-      для определения стоимости бизнеса, особенно при ог- танные нами мутильпликаторы, применяемые в соста-      раниченных условиях оценки.

ве сравнительного подхода, могут служить ориентиром