Пристенная модель переноса напряжений Рейнольдса на основе данных прямого численного моделирования

Дифференциальные модели для напряжений Рейнольдса. (Differential Reynolds stress models — DRSM), впервые появившиеся в литературе в середине XX века. [1, 2], являются сегодня одним из самых перспективных классов моделей турбулентности [3]. Главным образом, это связано с потенциалом DRSM-моделей в описании отрывных течений, повсеместно встречающихся на. практике, и осознанием ограничений популярных моделей турбулентности, основанных на гипотезе Буссинеска [4].

Рассмотрим уравнения Навье-Стокса для несжимаемой жидкости, осредненные по Рейнольдсу (здесь и далее по повторяющимся индексам ведется суммирование):

эи _ ₀ эи у dUi _ ¹ эр Эии _v d^Ui дх_і , dt ^j Эх j р дх_і Эх j Эх j Эх j

Здесь U_i — средняя скор ость жидкости, Р — среднее давление, р — плотность (константа), и — коэффициент вязкости (константа), Ui — пульсация скорости, черта — символ осреднения по Рейнольдсу. Тензор UiUj называется тензором напряжений Рейнольдса и описывает средний эффект турбулентного переноса импульса.

В моделях класса DRSM напряжения Рейнольдса определяются из решения уравнений в частных производных, структура которых точно выводится из уравнений Навье-Стокса. Эти уравнения содержат члены, требующие дополнительных замыкающих соотношений. Один из таких членов, который является объектом исследования для данной работы, — это тензор тройных корреляций скорости UiUjи^ • Он описывает средний эффект турбулентного переноса напряжений Рейнольдса пульсациями скорости.

В литературе можно найти несколько работ, посвященных моделированию турбулентного переноса напряжений Рейнольдса [5-12]. Одни из наиболее известных — модель Ханьялича и Лаундера [5] и модель Меллора и Херринга [6]. Эти модели были объединены и дополнены членами, содержащими градиенты средней скорости, в работе [13], где помимо прочего вводится глубоко математически обоснованная теория использования тензорных величин для адекватной начальной формулировки модели. Результаты последнего исследования были расширены в работе [14], посвященной моделированию турбулентного переноса скалярного параметра. Несмотря на все усилия, уровень точности моделей тройных корреляций скорости оставляет желать лучшего [4], и любые продвижения в этой области представляют интерес с точки зрения практического моделирования турбулентности.

Данная статья продолжает это направление исследований. Внимание уделяется моделированию тройных корреляций скорости в турбулентном течении вблизи стенки по современным данным прямого численного моделирования (Direct Numerical Simulation — DNS) течения в канале [15] в диапазоне чисел Рейнольдса 180 < Re_T< 5200. Здесь Re_T = U_Th/v — число Рейнольдса, вычисленное по динамической скорости U_T = ( t _w /р)¹/ ^и полувысоте канала h,T_w — трение на стенке. Интерес к пристенному моделированию турбулентности связан с активным развитием гибридных методов расчета турбулентных течений, в которых вблизи стенок решаются осредненные по Рейнольдсу уравнения Навье-Стокса, а в развитой турбулентности — уравнения метода крупных вихрей (Large Eddy Simulation — LES) [16].

Структура данной статьи следующая. В разделе 2 на основе [13] и [14] формулируется «базовая» модель. В разделе 3 к базовой модели добавляется тензорный член иной физической и математической природы, а также производится выделение нескольких расчетных областей на основе изучения коллинеарности вектора турбулентного переноса и векторов выбранного ранее тензорного базиса. Раздел 4 посвящен описанию нового метода калибровки, направленного на снижение зависимости калибровочных коэффициентов от числа Рейнольдса и придание модели большей универсальности. В разделе 5 приводится сравнение профилей тройных корреляций, полученных с помощью априорно откалиброванной по данным DNS модели, с данными DNS и одной из стандартных моделей турбулентного переноса [17]. На основе полученных результатов предлагается несколько вариантов дальнейшего развития модели.

2.    Описание и исследование базовой модели

Точное уравнение для тензора напряжений Рейнольдса в несжимаемой среде имеет следующий вид [4]:

du-iUj     O

Ot    Oxk

_____тт . _______ ^vui^u j UiUjUk + UiUju_k -т,"^ ^^s—' 2 OX^

гз k

⏟

___OU ,

"/'Д '

Oxk

-

__OU

Uj "k

Oxk

-

1 U^ X+U,    - (2, p у Ох,     Oxi) у

⏟⏞  ⏟

Oui Ou, Oxk Oxk

-

v O2UiUj

2 OxkOxk

)

Рал

Г гз

П із

e h. ^гз

В это уравнение входят:

Pi, — производство напряжений (не требует полуэмпирического замыкания);

П і, — корреляция «скорость - градиент давления»;

Е^- — «однородная» часть тензора скоростей диссипации напряжений;

Tijk — тензор турбулентных потоков напряжений Рейнольдса под действием пульсаций скорости.

Обратимся к тензору Ti,k = UiUjUk. Следуя работе [14], начнем с модели этого тензора вида k2 OUiUj         к____OUiUj

і ' + CHL-rUk ui -^- + Е^ Ox_k         Е^      Ox_i

UiUjUk =

-

^ ( cmh

{ i ^ j ^k} ^X

^{к    O}uUj    , Р    ^OuinJ \

^{+ C gu S} "охр ^{+ C gu} i^^^ki "OXT) ■               ⁽¹⁾

Здесь символ X, { _i ^ j ^ k } A_ijk = A_i,k + Ajk_i + A^, обозначает суммирование по циклическим перестановкам индексов, к = UiUi/2 — кинетическая энергия турбулентности, е ^һ = ЕД2 — «однородная» скорость ее диссипации, Si, и Uj — тензоры скоростей деформации и ротации соответственно:

^Sij =

1 оип ₊ оид     = i (up - оид

2 Ох ,    Ox_i , ^ij 2 Ох ,    Ox_i ‘

Модель (1) содержит эмпирические коэффициенты C mh ,C hl ,C gu ,C' _gu, которые могут быть константами либо функциями инвариантов введенных выше тензоров [4]. В данной работе калибровка модели проводилась по данным DNS о развитом турбулентном течении в канале [15]. Это — строго тонкослойное течение, направленное вдоль оси х, средние параметры которого зависят только от у. В таком случае в уравнения для UiUj входят лишь 4 из 10 возможных тройных корреляций скорости:

U2V, v3,vw2,uv2.

В тензорах скоростей деформации и ротации ненулевыми являются два компонента:

	0	1 dU 2 Әу	0		0	1 8U 2 Әу	0
Sij =	I 1 9U 2 Әу	0	0 1 ’	^ij =	1    1 әи 2 ду	0	0
	0	0	0		0	0	0

Это делает невозможным независимую калибровку коэффициентов Cgu ^и C' _G u- выражения при этих коэффициентах пропорциональны друг другу. Поступим, как предлагается в [13]: приравняем C gu ^и C'_G u друг другу. Тогда модель примет вид, который назовем «базовым»:

UiUjUk =

-

^  /      ^k2 ^Oui^u,       ^{к    Ou}i^u, _г^{к OU}k ^Oui^uj \     z₉x

(^Cmh 7"X7T ^{+ C hl} 7*^UkUi"aXT ^{+ C gu} (U"XP ' ⁽²⁾ { i ^ j ^ k }

Здесь первое слагаемое позаимствовано из модели Меллора и Херринга (далее — МН) [6], второе - из модели Ханьялича и Лаундера (далее — HL) [5], а третье было предложено в работе [13] и связано с градиентами средней скорости (далее — GU). В приведенной формуле сомножители перед тензорными величинами имеют смысл масштабных коэффициентов, подобранных исходя из физических соображений: они содержат в себе характерные величины, связанные с крупномасштабной турбулентностью, которая и определяет турбулентный перенос.

Если подставить в (2) все величины из DNS для некоторой точки у⁺ = const в пограничном слое, то получится переопределенная система из 4 уравнений на 3 неизвестных: Смн ,C hl ,C gu- Ее можно решить, например, методом наименьших квадратов. Однако расчеты по базовой модели выявили два существенных недостатка такого подхода.

Первый из них связан с особенностью поведения компонент пульсаций скорости при у⁺ ^ 0 [4]:

и ~ у⁺, ,v ~ (у⁺)², ш ~ у⁺.

Исходя из этого можно ожидать, что тройные корреляции при у⁺ ^ 0 имеют следующую асимптотику:

и²г ~ (у⁺)⁴, v³ ~ (у⁺)⁶, vw² ~ (у⁺ )⁴, иг² ~ (у⁺)⁵.                 (3)

Эта асимптотика была проверена по данным DNS течения в канале при ReT = 2000. Была построена аппроксимация зависимости ln uiUjUk от ln у+ в диапазоне 0 < у+ < 1, которая показала, что и2г ~ (у+)3'90, v3 ~ (у+)5'60, гш2 ~ (у+ )3’93, иг2 ~ (у+ )4’81.

Это близко к теоретически ожидаемым степеням. Значит, асимптотики (3) можно считать верными и использовать их для изучения поведения коэффициентов Смн ,C hl ,C gu ^пР^и у⁺ ^ 0.                              ___

Рассмотрим теперь уравнение для u2v:

u²v ~(у+)4

к² ди²

^-СМН ;., Е^ ду ⏟⏞

~<У+)5

к \^Эи²   __диг!         к³    ЭС диг

^{- hl} У ^v Уу ^{+ иг}1у ^{- gu} (Z^y • ² ау^У . ⏟   ⏞       ^⏟⏞

~(у+)7

~(У+)8

Здесь помимо (3) на основании [4] используется также асимптотика кинетической энергии турбулентности: к ~ (у⁺)², и «однородной» скорости ее диссипации: е ^ ~ (у⁺)⁰- Видно, что при у⁺ ^ 0 хотя бы один из коэффициентов должен иметь асимптотику

Смн ~

1 у+’

^Chl ~ Ул' ^Cgu ~ (у+)⁴'

то есть неограниченно расти при у⁺ ^ 0. Аналогичные результаты получаются и для остальных компонент тензора Tijk- Попытки калибровки базовой модели подтвердили эту гипотезу, а именно, показали сингулярность коэффициентов вблизи стенки.

Устранить подобную сингулярность позволяет изменение масштабных коэффициентов при тензорных величинах в (2). Идея состоит в том, чтобы достаточно сильно понизить степень этих коэффициентов по у⁺. Это может позволить повысить степень Смн , C hl , C gu по у⁺ вблизи стенки до неотрицательной. Заметим, что в развитой турбулентности к/Е^ — характерный масштаб времени крупных вихрей. Вблизи стенки величина к/Е^һ может стать меньше временного масштаба Колмогорова ( у/е^ )^1/2, что делает к/Е^һ непригодным выражением для определения масштаба времени. Чтобы избежать этой проблемы, в [14] предлагается использовать «гибридный» масштаб:

T = max

( -^Ст        •

где Ст = 6 — эмпирическая константа [18]. Ctj эемясь избежать излома в профиле Т. порожденного функцией max, мы решили определить характерное время крупных вихрей как корень из суммы квадратов величин k/e^h и временного масштаба Колмогорова:

Т =

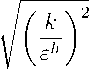
+ СТ £.

Покажем, что «гибридный» масштаб времени может позволить избавиться от проблемы сингулярности, если включить его в модель (2) следующим образом:

u2v ~(у+)4

-Смн kT— - C hl Т оу

⏟⏞

~(у ⁺ )3

du2  „__дин н2—--+ 2uv —— ду       ду

- C gu кТ ² • 2

~($/+) ⁵

⏟⏞

~(-у+')4

OU дин ду ду

Видно, что при у+ ^ 0 хотя бы один из коэффициентов должен иметь асимптотику:

^С мн ~ у⁺,

^Chl ~ УЙ ■

^C gu ~ 1.

Модель может обеспечить регулярность коэффициентов за счет членов при Смн и C gu- Однако уверенности в том, что коэффициент C hl будет при этом регулярным, по-прежнему нет. Решение системы (2) с новым временным масштабом Т дает профили коэффициентов, представленные на рис. 1 (течение в канале, Re_T = 2000). Видно, что теперь сингулярности при у⁺ ^ 0 не наблюдается.

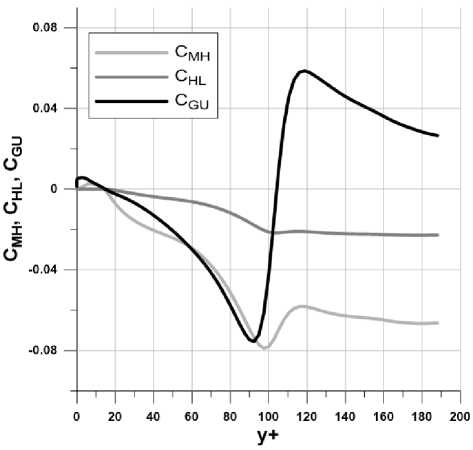
Рис. 1. Поведение коэффициентов модели (2) с «гибридным» масштабом (4) вблизи стенки канала.

Однако на рис. 1 виден второй недостаток базовой модели. В области вблизи у⁺ = 100 наблюдается странное поведение коэффициента C gu^ ^а именно, весьма резкое, нефизич-ное изменение значения на. почти противоположное. Это могло быть связано с тем, что в рассматриваемой области наблюдалась сингулярность коэффициента C gu^ которая сглаживалась за. счет решения системы уравнений методом наименьших квадратов.

Проблему можно попытаться решить введением новых независимых слагаемых в модель (2). Поиск привел к включению в модель члена, вида.

Ui Uj Uk = ...

-

∑︁

{ i ^ j ^ k }

CGekkT ujuk

д д$і

( к )) •

Влияние такого расширения модели будет рассмотрено в следующем разделе.

3.    Формулировка окончательной модели

Идея введения члена вида (5) состоит в том, что в него входит градиент не от тензорной, а от скалярной величины, то еств он имеет иное физическое и математическое значение. По этой причине данный член потенциально может скомпенсировать недостатки базовой модели в тех областях, где они имеются.

Решение системы уравнений модели (5) дало профили коэффициентов, изображенные на рис. 2. При этом система уравнений из четырех уравнений с четырьмя неизвестными по-прежнему решалась методом наименьших квадратов, поскольку точное решение не допускала существующая в какой-то области сингулярность. Из полученных профилей видно, что поведение коэффициента C gu ^пР^и члене с градиентами средней скорости немного улучшилось, но все еще существует необъяснимо резкий переход через ось абсцисс в области у+ = 100.

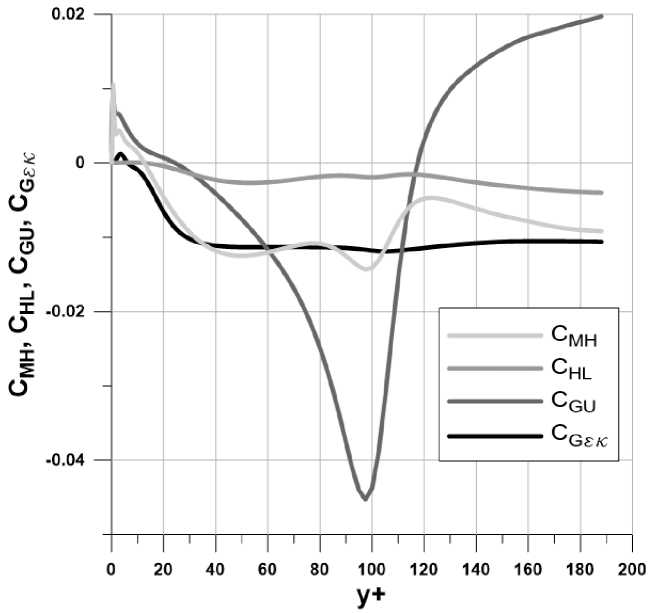
Рис. 2. Поведение коэффициентов модели (5)

Поскольку основная проблема связана с некорректным решением системы линейных уравнений в некоторых областях, то для более глубокого понимания причин этого явления мы решили изучить «коллинеарность» векторов левой и правой частей. А именно, четырехмерного вектора, состоящего из компонент турбулентного переноса (шТй, vvv, wwv, Uvv) с базисными векторами: