Проблемы обучения построению математических моделей в системе школа - колледж - вуз

Л/.5. Яшгсшшл аснхуиги/и Ktir^c'r^w (Jw/^epwipt^^ ур^щ/сщщ МГУ «m. Я Г ГЛ^^гга.

Н.К. Сорокина, Joymm кск£е<)ры с?бвде?7 j)?^w^

МГУ иль Я Я О^р^^гл,

ГЛ. Шиг/НРАИ, Л^О^СССТ^ Кй^ед/?Ы .МС/ОТИМО/ПЫЛ-И Г/ теРреТИМЧССЛОЫ .н^лгй^кк Л/ГУ ?ли. ЛЛ Огарева, д. я щ ешшюм, зав. кафедрой дифференциальных уравнений МГУ им. Я. Я. <Л?йр£вд.

Е, В. НГенциюва, до цени) кафедры информатики и вычислительной техники МГУ им. Я. П. Огарева

Одной из осееовпых целей высшей школы является подготовка твои чески мыслящих специалистов, способных решать новые задачи в науке, технике и производстве, Достижению этой цели служит овладение студентами методологией исследований в результате изучения диалектики, логики и теории познания в их единс тве и особенностях, a j а кжс в 11 ро цсссе ре ш е г гм я пра кти -ческих задач.

Опыт показывает,, что на «стыке» таких звеньев системы образования, как школа. колледж, вуз, образуется «педагогический барьер». ] крутому возникай проблема преемственности обучения в рамках указанной системы. Содержаниедействующих отечественных государстве иных стандартов и программ обучения нс в достаточной степени направлено на решение Проблемы преемственности и обеспечение преемственности как процесса. Покажем это на примере темы «Дифференциальные уравнения» в курсе математики для школы, колледжа н вуза.

Обрат имся к учебнику «Алгебра и начала анализа» для Ю — Г-х классов средней школы авторов Ш.А. Алимова и др,, в котором только один, заключи j ельный, параграф посвящен дифференциальным урав-нсшшш, Дифференциальное уравнение в нем определяется как уравнение, содержащее производную неизвестной функции. Далее говорится о том. что решение многих физ^ичес ких, иhoj i о i ичсс кiix, технических и других практических задач сводится к решению дифференциа гьного урм i ici 1 ия jc = kx, где А заданное число. (R физических и технических задачах независимой переменной, по которой производи гея дифференцированней является время. Время принято обозначать через Л искомые (неизвестные) функции через Xy^Z и т.д., а производные функций по / точками

.х=   ,Л' = ——

dt (/Л

И Т-Д.)

Решениями этою уравнения являются фуТЖГПД!

х “Cl³

где С - постоянная, определяемая условиями конкретной задачи.

Затем в качестве иллюстрации рассматриваются два примера.

Пример J. Скорость ?й(/) размножения бактерий связана с массой w(0 бактерий в момент времени f уравнением m(f) = Am(Z)_?

где £ -положительное Число, зависящее от вида бактерий и внешних условий, -

Решениями этого уравЕ<ения являются ' функции

m(0 = Ce^h

Постоянную С можно найти из условия. что в момент f = О масса бак серий Тол известна. Тогда

т(0) = №0 = с^0 - с, И поэтому

?и^) = тое^

Л^миер 2. Задача О радиоактивном распаде.

Нели т(/) - скорость радиоактивного распада в момент времени ^, то m(t) - -£m(f), где' А - постоянная, зависящая от радиоактивности вещества. Решениями этого уравнения являются функции

/и(г) - Се

Если в момент времени f масса равна m_fi, то С = Я%_? и поэтому

т(0 = т^е

В качестве приложения к теории дифференциальных уравнений приводится дифференциальное уравнение гармонических колебаний:

Х = -<У²Х_? где _fy — заданное пол ожите лъп ое ч пел о.

й^Х

Функцию “У называют птоеюй про-с/Г изводной функции х(/)и обозначают х(г) или х. Решениями уравнения являются функции

ДС(Г) = C1sin(fiJ# + C2), где С,,С2 — постоянные, определяемые условиями конкретной задачи.

Эго уравнение называют уравнением гарм см । ическнх колебаний.

Как видно из приведенного фрагмента, рассмотрение темы «Дифференциальные уравнения» в школе происходил на отдельных примерах с физическим содержанием.

То же самое наблюдается и в классах с углубленным изучением математики, а также в колледже. Обучение там осуществляется по учебникам М.И. Башмакова «Алгебра и начала анализа» и НЯ, Виленкина и др. «Алгебра и математический анализ».

Одна из заключительных бесед в учебнике М.И. Башмакова посвящена составлению дифференциалы еьгк уравнений. Диф-феринонильное уравнение здесь вводится как уравнение, связывающее неизвестную функцию и ее производные. Пояснение эп> io ПОНЯТИЯ происходит так же ла примерах уравнения механического движения и радиоактивного распада.

Далее, в обоих учебниках дается определение решения дифференциального уравнения: решением дифференциального уравнения называют любую функцию^ при подстановке которой в это равнение получается тождество. Затем в учебнике М.И. Башмакова приводятся примеры решения написанных выше уравнений без всякой ссылки на какие-либо изученные ранее методы решения уравнений.

• 1)    ФУНКЦИЯ X =    + Vg^ + Ху.

где V^3 Xq - произвольные числа, является решением уравнения X = а. Дсйстви- тг тепьно, вычисляя производные, получаем

Л" - at 4- Vq , X - Я

1 £

• 2)    Функция X = И sinf ¹ -йп'к

где Л и а - произвольные числа, является решением уравнения

А

X = - - х.

т

Решение уравнений показательного роста и гармонических колебаний приведено более подробно, но также без указания методов решения, в условиях отсутствия ориентировочной ОСНОВЫ ДЛЯ адекватного выбора метода решения, без должного обоснования полученных результатов и без пере пол а решении на язык реальных процессов.

В дополнение к определению решения дифференциального уравнения в учебнике Н Я. Виленкина предлагается определение общего и частного решения дифференци ального уравнения, вводится понятие особой точки. 41 о касается методов интегрирования дифференциальных уравнений, to здесь рассматривается интегрирование дифференциального уравнения с разделяющимися переменными. Но и в этом учебнике не затрагивается вопрос о существовании и единственности решений задачи Коши дифференциального уравнения. не осуществляется перевод полученных математических решений на язык реальных процессов.

Из приведенных фрагментов мож его сделать вывод, что ни в школе, ни в колледже тема «Дифференциальные уравнения» не рассматривается ряде по ложен но, отсутствует логическая организация учебного материала по этой теме. В итоге па каждом згалс системы школа - колледж -вуз данная тема наполняется лишь предметным содержанием, что, естественно, не .позволяет учащемуся самостоятельно познать диффере11!П1плЕ₁пг.1е уравнения как модель определенного реального процесса и изучить методы их решения.

Ниже предлагается фрагмент логической организации учебного материала в системе школа - колледж - куш

• I)    дифференциальное уравнение как модель реального процесса;

• 2)    теорема существования и единственности решений задачи Коши;

• 3)    выбор соответствующего метода решения (реализации модели),

• 4)    реши шс диффереж шалы юго уравне ния как совокупность определенных действий:.

• 5)    разъяснение решений на языке мс-дсляровапнл реального процесса.

Здесь и далее предполагается, что «вуз» - это «технический вуз».

Приведем фрагмент реализации построенного модуля обучения.

ДифферснциалытЕлм уравнением называется уравнение, связывающее независимые переменные, их функцию и производные этой функции. Если независкмая переменная одна, то уравнение называется обыкновенным. Если независимых переменных две или больше, то уравнение называется дифференциальным с частными производными. В данной статье рассматриваются обыкновенные дифференциальные уравнения, причем как независимая переменная, так и искомая функция пред-пол аг аю те я в еществен ними.

Наивысший порядок производной, входящей в уравнение,.называется порядком дифференциального уравнения. Например:

• I)    ^JC 4- 4^ = X⁵ - обыкновенное дифференциальное уравнение I ч о порядка;

• 2)    -X — 5Ц'4-X — ?- обыкновенное дифференциальное уравггеп ис 2-го ппрящга.

Рассмотрим дифференциальное ураы-неггие dt

Решим его. Для ^тиго перепишем данное уравнение в виде dx= f(tWY

Теперь можно цроинтегрировагь левую и правую части, те.

Jdk = J/(0^ + C

В результате получим решение дифференциального уравнеЕтия (1):

X = /ЛОЛ + С.

Следующим рассмотрим уравнение

"Г = ^)-         (2)

я/

Перепишем это уравнение в виде dx

= dk <р(х)

интегрируя левую н правую части, получим , dx

I-----~ I + С.

очевидно, здесь ^>(х) ^ 0.

Как следует из примеров, решение дифференциальных уравнений сводится к интегрированию- Поэтому вместо «решить дифференциальное уравнен не» можно говорить «проинтегрировать дифференциальное уравнение».

Дифференциальное уравнение, полученное е результате исследования какого-либо реального явления или процесса, называют динамической моделью этого явления или процесса. Динамические модели-частный случай множества математических моделей, которые могут быть построены при изучении окружающего нас мира. В процессе построения обыкновенных дифференциальных моделей важное значение имеет знание законов той области науки, с которой связана природа изучаемой задачи . 1 ак, например, в механике это могут быть законы Ньютона, в теории электрических цепей-законы Киргхофа и Ома, в теории скоростей химических реакций - закон действия масс., и тд.

Наша цель в конем ном счете состоит в ■том, чтобы на примерах (содержательных, а не иллюстративных) из различных областей знания показать возможности исполь-зова! 1 ия обыкновенных дифференциальных уравнений в процессе познания окружаю щей нас действительности. Параллельно с этим требуется дать определение решения, показать игл и чител ьные особен!юсти дифференциальных уравнений, рассмотреть некоторые методы решений, указать, каким образом можно осуществить преемственность в указанной системе. Приведенные ниже примеры взяты из следующих источников: Эрроусмит Ц., 11лейс К. Обыкновенные дифференциальные уравнении. Качественная теория с приложениями. М., 1 986; Гутер Р.С, Ян польский А.Р Дифференциальные уравнения: Учеб, пособие дня втузов. 2-е изд , перераб. и доп. M.d 1976.

ilpititep J. Предположим, что масса поддерживается вертикально расположенной пружиной. Допустим, что масса может смещаться только вдоль оси пружины и, кроме того, она связана с поршнем, который движется в цилиндре, заполненном жидкостью и помещенном внутри пружины. Такое устройство являйся идеализированней моделью амортизатора.

Обозначим через Л’ смещение массы т вниз от положения равновесия.

Пусть:

• а)    на массу действует сила К (закон Гука), А > 0, направленная в сторону положения равновесия;

• 6)    сила, с которой поршень действует на массу и которая препятствует ее движению, пропорциональна кинетическому моменту /^ с коэффициентом 2АД > 0.

С- учетом того что р. ~ MX и скорость изменения кинетического момента данной массы равна приложенной к ней силе (второй закон Ньютона), уравнение (1) можно записать следующим образом:

p = -Ky*x)-2]p + mg, (3) где / ■ длина пружины в положении рав-новесия. Но в положении равновесия р = р = % = 0. Следовательно,

Ki = mg.

Тогда дифференциальное уравнение (3) примет вид р =± ^х = -Кх - 2Яжг.

Окончательно имеем х + 2^ + <ы0 х = 0.(4)

2£ где ^.-

Решение дифференциальною уравнения (4) X = A? ^ sin(^._n/ + 5) определяет зако । юмертюсть кол ебател гл гых л в и жений амортизатора. Здесь Лё - амплитуда колебаний, гЯд — часто j а колс 5 аний, 2) ^-начальная фала.

Как видно из решения, ио мерс роста времени Г амплитуда уменьшается, АрдмсТ? 4. Теплопередача через трубу. ПустЕ» имеется толстая цилиндрическая труба, внутренний радиус которой ра-еен г. а внешний А7 Нужно определить теплопередачу через трубу изнутри наружу Предполагается при этом, что установился стационарный тепловой режим, т.с, количество тепла, проходящего через какую-либо дае гнуто площадь, постоянно.

В теории теплонроводности считается, что количество тепла, проходящею через бесконечно малую площадку перпендикулярную к некоторой оси, в направлении ЭТОЙ оси за промежуток времени dt, пропорции* иапьно шюшади ^^ площадки, длительности промежутка и скорое] и падения температуры в этом направлении., т е.

dq - -ZdF — dt. dn

Здесь О есть температура трубы, знак «минус» указывает, что поток тепла движется в стороЕгу падения температуры, постоянный коэффициент 2 зависит от вещества рассматриваемого тела и налы лается коэфф и циентом теплопроводности.

Выделим внутри трубы цилиндрическую поверхность радиуса p-l'* < /^ < R. Тогда для элемента ^F этой поверхности ^70

А/ - - AY/*    dr. f^

dp

Количество тепла нс зависит ни от элемента dR". пи от промежутка време ни <7/ Просуммировав выражсЕгия типе (5), получим полное количество тепла для всей поверхности цилиндра за единицу времени

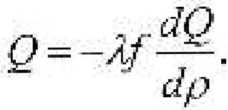
Если длина Трубы равна /, то / = 2^й/, так что

, ч ™ , dQ

Q = -2,^p — .     (6)

dp

Поскольку процесс передачи тепла является установившимся, т.с. тепло нс может накапливагься ни в какой части трубы, то величина О не Зависит от

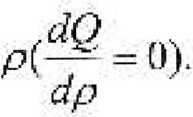
Г 1родиффсрепцировав равенство (6) но ^Э, получим дифференциальное уравнепис второго порядка вила dp" dp

ИНГС] рируя это уравнение, можно получить решение, которое описывает изменение температуры точек трубы в зависимости от их расстояния от оси.

(()кончт1ие следует)