Профессиональные математические компетенции студентов вуза, формируемые при изучении учебной дисциплины "Математический анализ"

исследовательской, научно-изыскательной, производственно-технологической, организационно-управленческой, преподавательской деятельности. Отмечается, что «бакалавр по направлению подготовки 010100 Математика должен решать профессиональные задачи в…: научно-исследовательской и научноизыскательной деятельности (применение основных понятий, идей и методов фундаментальных математических дисциплин для решения базовых задач; решение математических проблем, соответствующих квалификации, возникающих при проведении научных и прикладных исследований…); производственно-технологической деятельности (использование математических методов обработки информации, полученной в результате экспериментальных исследований или производственной деятельности, применение численных методов решения базовых математических задач и классических задач естествознания в практической деятельности…); организационно-управленческой деятельности (применение математических методов экономики, актуарно-финансового анализа и защиты информации…); преподавательской деятельности (преподавание физико-математических дисциплин и информатики…, участие в разработке различных методов тестирования для оценки успеваемости учащихся)».

В качестве пояснения по каждому виду деятельности приведен перечень соответствующих профессиональных компетенций (всего их 29).

Исследование будет проводиться для основной образовательной программы бакалавриата 010100.62 – Математика , т.к. для этой программы учебная дисциплина « Математический анализ » является профилирующей.

В структуре ООП бакалавра по направлению подготовки 010100 – Математика в профессиональном цикле в базовой (общепрофессиональной) части предполагается формирование следующих 13 профессиональных компетенций из указанного перечня, а именно:

• •    умение формулировать результат ( ПК-3 );

• •    умение строго доказать утверждение ( ПК-4 );

• •    умение грамотно пользоваться языком предметной области ( ПК-7 );

• •    умение ориентироваться в постановках задач ( ПК-8 );

• •    знание корректных постановок классических задач ( ПК-9 );

• •    понимание корректности постановок задач ( ПК-10 );

• •    понимание того, что фундаментальное знание является основой компьютерных наук ( ПК-12 );

• •    выделение главных смысловых аспектов в доказательствах ( ПК-16 );

• •    владение методами математического и алгоритмического моделирования при решении прикладных задач ( ПК-20 );

• •    владение методами математического и алгоритмического моделирования при анализе теоретических проблем и задач ( ПК-21 );

• •    владение проблемно-задачной формой представления математических знаний ( ПК-22 );

• •    умение самостоятельно математически корректно ставить естественнонаучные и инженерно-физические задачи ( ПК-25 );

• •    возможность преподавания физикоматематических дисциплин и информатики в средней школе и средних специальных образовательных учреждениях на основе полученного фундаментального образования ( ПК-29 ).

По ФГОС математиков «в результате изучения базовой части цикла студент должен иметь базовые знания в области фундаментальной математики и компьютерных наук; уметь формулировать и доказывать теоремы, самостоятельно решать классические задачи математики; владеть навыками практического использования математических методов при анализе различных задач».

В блоке дисциплин профессионального цикла находится и базовая, профильная для бакалавров-математиков, дисциплина «Математический анализ». Это означает, что изучение математического анализа должно способствовать формированию перечисленных выше профессиональных компетенций, которые, однако, в своей законченной форме устанавливаются лишь к завершению всего процесса обучения, и трудность их диагностирования и контроля на младших курсах указывает на необходимость вычленения из них трансформированных профессиональных математических компетенций .

Исходя из опыта научно-практической деятельности авторов данной статьи и имеющихся на сегодняшний день исследований по компетентностному подходу в обучении, предлагаем перечень профессиональных ма-

Структурная матрица формирования профессиональных математических компетенций в соответствии с ФГОС ВПО направления подготовки 010100.62 – Математика по учебной дисциплине «Математический анализ»

5 s >s 40 a. 5 „ 3 Я £ - о 3 у е + + + + + + + + + U On ^ в CO S 4 5 -< « s и В s H -< S H -< S a H >S Г4 5 s >s in у S S а а ч а ч ч a е g В 2 s 3 5 в в g е 5 а 1 о ч S g + + + + + + + 5 s >s 4 я      « gosS5«y§ чищнчязд 55 м о « о 3 £» ££ ^в 3        3 S      S + + + + + + + + © >s m s   а у 2 О   В S о 5 S 2     о ч   5 5     « в   g а s 3 « а 5 5 в ф в   в 2 а а 5     s s в е в Щ С   g S 5 5    В 4 в ° g-K £ + + + + + + + + + + + + + a H © >S rH © >s rq я   5 а   н я В о Я 5 1 S 55          а в § 111 S £ К I I В яе ч в е е + + + + + + + + £ 5 s >s rH я а   а 2 о в 55 о    2 а в 5 и S   а   в Э      3 Й ч 3 Ч 3   м Ч а у a s   в s s « « 5 3 Н а 0 2   ч   ч о с о я   я + + + + + + + ^ Л CL h U © £ № О S £ „ 2 = б < « а 2     X 41 У у О S S е и я В eq У в со у в тГ й в ш а в 4© й в в 00 в у в о в в в в тематических компетенций (ПМК), которые, на наш взгляд, во-первых, отслеживаемы и диагностируемы, во-вторых, показывают динамику формирования «глобальных» профессиональных компетенций, на базе которых они были сконструированы и преобразованы.

Профессиональные математические компетенции – это комплекс специфических предметных знаний и мыслительных умений, практических навыков, опыта деятельности и структурированных способностей [2] , а именно:

• •    владение математической культурой и математической грамотностью ( ПМК-1 );

• •    свободное использование математической символики и обозначений ( ПМК-2 );

• •    понимание главных и дополнительных параметров в условии поставленной задачи/ проблемы ( ПМК-3 );

• •    формулирование корректной постановки математической задачи/проблемы и выделение некорректности в условии или решении задачи ( ПМК-4 );

• •    видение практической проблемы и соотнесение с ней фактического теоретического материала ( ПМК-5 );

• •    выдвижение гипотезы и осуществление мысленного упреждения действий ( ПМК-6 );

• •    использование приемов аналогии, обобщения, противопоставляющей (расчленяющей) абстракции и переноса ( ПМК-7 );

• •    способность использовать различные элементы математического знания при решении профильных или прикладных задач ( ПМК-8 );

• •    комбинирование известных элементов и компонентов с созданием их новых сочетаний и комбинаций ( ПМК-9 );

• •    использование компьютерных программ и программных оболочек в осуществлении профессиональной математической деятельности ( ПМК-10 );

• •    поиск альтернативы известному решению, творческий подход к решению сложных задач ( ПМК-11 );

• •    владение алгоритмическим, технологическим, системным подходом к решению поставленной задачи ( ПМК-12 );

• •    способность к анализу и синтезу в проводимых рассуждениях и вычислениях ( ПМК-13 ).

Если, к примеру, взять учебную дисциплину «Математический анализ» за 1-й курс (1–2-й семестры), то годовое содержа- ние этой дисциплины можно разделить на 6 учебных модулей (см. табл. на с. 115). Учитывая особое место дисциплины в профессиональном блоке, оправдана и определенная «загруженность» структурной матрицы формирования ПМК по каждому из 6 учебных модулей. Как видно из таблицы, ключевым звеном подготовки бакалавров математиков на 1-м курсе является учебный модуль «Дифференциальное исчисление функции одной переменной». Знания и опыт, приобретенные студентом при изучении именно этого раздела, в основном определяют дальнейшее совершенствование профессиональной математической подготовки студентов.

Нелегко подобрать и задания, которые объективно диагностируют ту или иную профессиональную математическую компетенцию. При оценке уровня сформированно-сти ПМК-2 можно, например, использовать элементарное задание вида:

• @ 1. С помощью математической символики записать заданное определение в более кратком виде:

Функция y = f ( x ) называется непрерывной в точке a , если для любого положительного числа ε найдется отвечающее ему положительное число δ такое, что для всех значений аргумента x, удовлетворяющих условию | x - a | < 5, справедливо неравенство | f ( x ) - f ( a ) | < £.

Предлагаемый вариант ответа (но не единственный, возможны некоторые другие вариации):

Функция y = f (x) называется непрерывной в точке a , если такое, что

• - ^ \ix;\x-a\<8 => | f(x) - f{a) |< 8.

Диагностирование уровня сформирован-ности ПМК-8 можно провести, например, с помощью профильного профессионально ориентированного кейс-задания, составленного по учебному модулю « Дифференциальное исчисление функции одной переменной », тема « Наибольшее и наименьшее значения функции » [3] .

1-я часть кейс-задания

Из квадратного листа жести со стороною а, вырезая по углам равные квадраты и сгибая края, составляют прямоугольную открытую коробку.

Какой из представленных ниже чертежей отражает условие задачи?

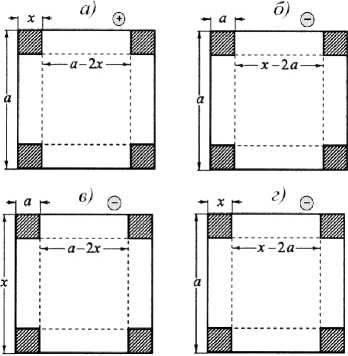
2-я часть кейс-задания

Какой вид будет иметь функция, характеризующая объем сделанной прямоугольной открытой коробки?

Вставитьответ: f ( x ) =            _

Правильный ответ: f ( x ) = x ( a - 2 x ) ² .

3-я часть кейс-задания

Как полчить коробку наибольшей вместимости? П ровест и исследование и найти значения всех искомых параметров.

Приводится развернутый ответ, напри- мер, в форме (вариант):

Обозначим сторону вырезаемого квадра- та через х. Тогда объем коробки выразится формулой у = х(а – 2х)2, причем х изменяет- ся в промежутке

0, ^a ₂

. Вопрос задачи свел-

ся к нахождению наибольшего значения функции у в этом промежутке. Так как производная у' = (a – 2x) (a – 6x) между значениями 0 и aa имеет единственный корень x = , то, убе дившись в том, что это значение доставляет функции максимум, одновременно получаем и a2

искомое наибольшее значение: x = y =

6,

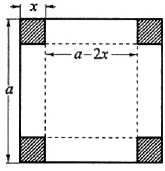
Приведенное кейс-задание является профессионально ориентированным, т.е. составлено на основе элементов не только математического анализа, но и других областей математического знания. Здесь студентам следует показать не только знания в области геометрического восприятия представленного материала, но и свои способности в использовании элементов исследования функции и нахождения ее экстремальных значений, которые были изучены ранее.

Аналогично конструируются задания для диагностики уровня сформированности других профессиональных математических компетенций.

Таким образом, введение в стандартах понятия «компетентность» как основополагающего результата профессиональной деятельности сказывается естественным образом на формах контрольных заданий и программнодидактических тестовых материалов. Специфика таких заданий и задач требует от ведущего преподавателя несколько иного подхода к планированию всего учебно-образовательного процесса, который включает обучение-учение, диагностику, коррекцию и совершенствование качества подготовки студента.