Прогнозирование доходов Финляндии с иностранных туристов на основе математических многофакторных моделей
Автор: Варламова С.А., Ефимова А.А., Кох К.Д.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (50), 2020 года.
Бесплатный доступ
Представлено исследование доходов Финляндии от прибывающих иностранных туристов. Выбраны социально-экономические факторы, которые могут оказывать влияние на систему. Построен ряд математических моделей, в качестве наилучшей по показателям аппроксимации и постпрогноза выбрана линейная многофакторная модель. С ее помощью сделан краткосрочный прогноз и исследована чувствительность доходов от прибывающих туристов к изменению управляемых и неуправляемых факторов. На основании результатов исследования сформулированы рекомендации по повышению доходности.
Моделирование, прогнозирование, финляндия, туризм
Короткий адрес: https://sciup.org/147245491
IDR: 147245491 | УДК: 004.92+379.85+338.48 | DOI: 10.17072/1993-0550-2020-3-29-33
Текст научной статьи Прогнозирование доходов Финляндии с иностранных туристов на основе математических многофакторных моделей
Туристическая индустрия Финляндии является одной из самых перспективных отраслей страны. Ранее властями страны было принято распоряжение о Стратегическом проекте улучшения туризма на период до 2020 г., начатой Министерством труда и экономики. Данная программа была направлена на контроль развития данной отрасли. Основываясь на отчетах по туризму [7], в последние годы для экономики Финляндии туризм стал более важным. На протяжении нескольких лет доходы от туризма составили примерно 14 млрд евро. К концу 2017 г. прибыль от туризма составляла 15 млрд евро, а посетившие страну туристы потратили около 4,6 млрд евро (5,2 млрд долларов). При этом, по сравнению с 2016 г., прямая валовая добавочная стоимость от туризма стала на 8 % больше. Также, по подсчетам, в 2017 г. в Финляндии насчитывалось 15,2 млн. ночевок местных туристов и 6,7 млн. ночевок иностранных туристов.
Цель работы – это изучение предметной области, построение математических многофакторных моделей и последующий выбор одной из них для прогноза дохода Финляндии с иностранных туристов.
Для работы был выбран критерий – доходы Финляндии от иностранных туристов [1] , а также были подобраны факторы, влияющие на данный критерий:
-
• количество людей, въехавших в Финляндию [4] ;
-
• количество работников, работающих в области туризма [5] ;
-
• количество спальных мест (в гостиницах, хостелах и тому подобное) [6] ;
-
• курс доллара к евро [7] ;
-
• количество краж на территории Финляндии [3] .
Выбранные факторы являются логичнообоснованными, так как каждый из них ока- зывает влияние на доходы страны от туризма.
Для построения моделей необходимо составить годовые ряды всех факторов и критерия.
Они приведены в табл. 1 .
Таблица 1. Годовой ряд факторов и критерия за 2009–2018 гг.
|
Названия факторов / год |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Доходы страны от туристов ( y , млн. долларов) |
4070 |
4497 |
5612 |
5419 |
5774 |
|
Количество въехавших в Финляндию ( x 1 , тыс. человек) |
2220 |
2319 |
2623 |
2778 |
2797 |
|
Количество работников ( x 2 , люди) |
51200 |
49100 |
49600 |
52000 |
50500 |
|
Количество спальных мест ( x 3 , койко-места) |
58061 |
58483 |
60408 |
61953 |
62405 |
|
Курс доллара к евро ( x 4 , евро) |
0,77 |
0,69 |
0,77 |
0,76 |
0,74 |
|
Количество краж ( x 5 ) |
19186 |
32102 |
33032 |
28765 |
22911 |
Таблица 1 ( Продолжение )
|
Название факторов / год |
2014 |
2015 |
2016 |
2017 |
2018 |
|
Доходы страны от туристов ( y , млн. долларов) |
5407 |
4009 |
4016 |
5207 |
5663 |
|
Количество въехавших в Финляндию ( x 1 , тыс. человек) |
2731 |
2622 |
2789 |
3180 |
3200 |
|
Количество работников ( x 2 , люди) |
50600 |
51800 |
52500 |
55400 |
56200 |
|
Количество спальных мест ( x 3 , койко-места) |
62777 |
63985 |
64075 |
68464 |
69002 |
|
Курс доллара к евро ( x 4 , евро) |
0,73 |
0,84 |
0,92 |
0,93 |
0,82 |
|
Количество краж ( x 5 ) |
24725 |
24659 |
24594 |
24482 |
24457 |
Для исследования можно применять различные модели, например линейномногофакторная модель, модель в пространстве состояний, авторегрессионная модель и линия тренда [9] .
В нашем случае выбор будет из двух моделей: линейно-многофакторная или модель в пространстве состояний:
-
• Линейная-многофакторная модель (ЛММ) – данная модель дает возможность изучить зависимость критерия от воздействующих на него факторов.
-
• Модель в пространстве состояний (МПрС) – данная модель открывает различные возможности в формализации процедур синтеза, анализа, а также автоматизации проектирования.
Для работы с факторами их значения были пронормированы, а также был проведен корреляционный анализ. Нормирование данных производилось по формуле, представленной ниже:
~ _ y ( t ) — y min
У max — У min
После того, как данные были пронормированы, производится корреляционный анализ по формуле:
-^X-xHyL-yL- rxy' vE(Xi -x)2 •£(y -y)2 ’ где x – среднее значение фактора, y – среднее значение критерия. Результат корреляционного анализа представлен в табл. 2.
Таблица 2. Значения корреляционного анализа
|
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
|
|
x 1 |
1 |
0,81043 |
0,94643 |
0,56975 |
-0,1017 |
|
x 2 |
1 |
0,896 |
0,70782 |
-0,39629 |
|
|
x 3 |
1 |
0,68929 |
-0,23939 |
||
|
x 4 |
1 |
-0,31954 |
|||
|
y |
0,54993 |
0,14105 |
0,30336 |
-0,27579 |
0,25668 |
В результате корреляционного анализа, был исключен фактор "Количество спальных мест", так как данный фактор имеет высокую взаимную корреляцию.
Для построения линейно-многофакторной модели была использована формула, представленная ниже:
y (t )= a 0 +X ia^ )’ где at, i = 1, N = - коэффициенты влияния i-х факторов на критерий, N – количество выбранных ранее факторов.
Чтобы определить коэффициенты, минимизируем квадратичное отклонение погрешности аппроксимации по следующей формуле:
S = Z t У ( t ) - У расч ( t )) 2 ^ min .
Для минимизации был применен мастер "Поиска решений" в программном обеспечении MS Excel . Полученные коэффициенты для ЛММ имеют следующие значения:
a 0 = 0,28256, a 1 = 1,63097, a 2 = -0,44145, a 4 = - 0,92975, a 5 = 0,01337.
Проанализировав коэффициенты, можно сделать вывод, что наибольшим из них является a 1 , а значит соответствующий фактор x 1 – "Количество въехавших в Финляндию" оказывает на систему большее влияние.
Данный результат является логичным, так как количество людей, которые въезжают в страну на отдых увеличивает доходы страны.
Наименьшим коэффициентом является a 4 , это означает, что фактор x 4 – "Курс доллара к евро" оказывает наименьшее влияние на систему. Так как Финляндия находится в безвизовой зоне Евросоюза, то большая часть ее туристов использует евро.
Квадратичная погрешность аппроксимации равна 0,2364.
Для построения модели в пространстве состояний необходимо воспользоваться системой, состоящей из двух формул. Запись системы представлена ниже:
Jx(tj a + B * X(t^) y(t ) = c + d * x(ti)
где B – матрица перехода внешней среды из одного состояния в другое, a и c – это свободные коэффициенты и d – вектор выхода.
Как и ранее, были найдены коэффициенты для модели в пространстве состояний через мастера "Поиск решений" в программ- ном обеспечении MS Excel. Квадратичная аппроксимация для модели равняется 0,2243.
Для дальнейшего прогнозирования необходимо выбрать одну из вышеописанных моделей. Выбор будет осуществляться, основываясь на результатах метода постпрогноза на несколько лет для каждой модели.
Графики, демонстрирующие постпрогнозы ЛММ (рис. 1) и МПрС (рис. 2) продемонстрированы ниже.
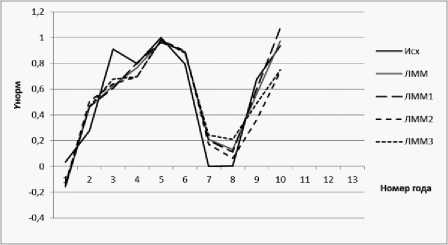
Рис. 1. Графики постпрогноза ЛММ
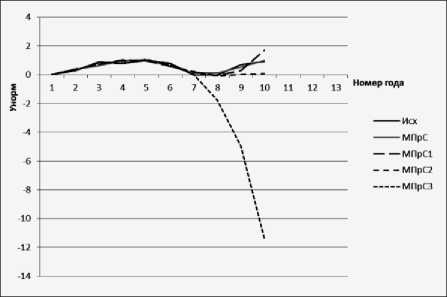
Рис. 2. Графики постпрогноза МПрС
Анализируя данные графики, приходим к выводу, что лучше выбрать ЛММ для дальнейшей работы с ней.
Построим прогноз доходов Финляндии с иностранных туристов по ЛММ на 2019–2021 гг., используя управляемые и неуправляемые факторы
Таблица 3. Прогнозы факторов и критерия
|
Номер года, t |
11 |
12 |
13 |
|
y |
1,15154 |
1,42439 |
1,69723 |
|
x 1 |
1,28463 |
1,50145 |
1,71827 |
|
x 2 |
1,25346 |
1,48020 |
1,70695 |
|
x 4 |
0,72911 |
0,70826 |
0,68741 |
|
x 5 |
0,37424 |
0,36904 |
0,36384 |
Далее будем исследовать развитие системы при изменении управляемых или неуправляемых факторов [2] .
Рассмотрим первый случай на двух управляемых факторах одновременно: первым фактором выберем количество людей, въехавших в Финляндию ( x 1 ), а за второй фактор примем количество работников ( x 2 ).
Произведем небольшие изменения данных факторов, на ±5 % и ±10 % и получим следующую таблицу (табл. 4):
Таблица 4. Прогноз при малых изменениях двух управляемых факторов
|
x 1 / x 2 |
x 2 -10 % |
x 2 -5 % |
x 2 +0 % |
x 2 +5 % |
x 2 +10 % |
|
x 1 -10% |
1,14197 |
1,04524 |
0,93777 |
0,819 |
0,68835 |
|
x 1 -5% |
1,50174 |
1,405 |
1,29753 |
1,17876 |
1,04812 |
|
x 1 +0% |
1,90144 |
1,8047 |
1,69723 |
1,57846 |
1,44782 |
|
x 1 +5% |
2,34317 |
2,24644 |
2,13897 |
2,02019 |
1,88955 |
|
x 1 +10% |
2,82905 |
2,73231 |
2,62484 |
2,50607 |
2,37542 |
При анализе данной таблицы, можно сделать вывод, что количество доходов Финляндии возрастет при увеличении потока туристов на 10 % (x1+10 %) и уменьшения количества рабочих на 10 % (x2-10 %), тем самым будет сэкономлен бюджет страны за счет меньших выплат заработной платы рабочим в области туризма.
Второй случай рассмотрим на одном неуправляемом факторе: курс доллара к евро ( x 4 ). Так же, как и в первом случае, произведем небольшие изменения фактора, на ±5 % и ±10 % и получим следующую таблицу (табл. 5):
Таблица 5. Прогноз при малых изменениях одного неуправляемого фактора
|
x 4 |
x 4 -10 % |
x 4 -5 % |
x 4 +0 % |
x 4 +5 % |
x 4 +10 % |
|
Реакция |
1,87043 |
1,78839 |
1,69723 |
1,59649 |
1,48568 |
При анализе данной таблицы можно сделать вывод, что количество доходов Финляндии может снизиться, если курс доллара к евро увеличится: из-за этого произойдет индексация заработной платы, что впоследствии увеличит расходы бюджета.
Доходы Финляндии с иностранных туристов растут – этот вывод был получен при рассмотрении данных, исходя из смоделированных систем.
Если на систему не будут негативно влиять неуправляемые факторы (например: курс доллара к евро, при увеличении которого (+10 %) бюджет будет наоборот уменьшаться из-за индексации заработных плат), то данный рост доходов будет продолжаться. Помимо неуправляемых факторов, на систему могут влиять и управляемые факторы.
Так, в ходе исследования была получена информация, что лицо, принимающее решение, может оказать влияние на управляемый фактор – количество людей, въехавших в Финляндию, увеличив данное число на 10 % путем упрощения визового режима для других стран, не входящих в безвизовую зону.
Также лицо, принимающее решение, может воздействовать и на второй управляемый фактор – количество рабочих, снижая их количество на 10 %: бюджет Финляндии будет экономить средства.
Список литературы Прогнозирование доходов Финляндии с иностранных туристов на основе математических многофакторных моделей
- Доходы Финляндии с иностранных туристов. URL: https://knoema.ru/atlas/Финляндия/topics/Ту ризм/Ключевые-показатели-туризма/Всего-доходов-долл-США/ (дата обращения: 03.06.2020).
- Затонский А.В., Сиротина Н.А. Преимущества дифференциальной модели сложной экономической системы // Образование. Наука. Научные кадры. 2012. № 8. С.98-102.
- Количество краж на территории Финляндии. URL: https://knoema.ru/atlas/_(дата обращения: 03.06.2020).
- Количество людей, въехавших в Финляндию. URL: https://knoema.ru/atlas/Финляндия/topics/Туризм/Показатели-въездного-туризма/Прибытия/ (дата обращения: 03.06.2020).
- Количество работников, работающих в сфере туризма. URL: https://knoema.ru/atlas/Финляндия/topics/Ту ризм/Прямой-вклад-туризма-в-занятость/Прямой-вклад-в-занятость-тыс (дата обращения: 03.06.2020).
- Количество спальных мест. URL: http://pxnet2. stat.fi/PXWeb/pxweb/fi/StatFin/ StatFin_lii_matk/statfin_matk_pxt_11iy.px/ (дата обращения: 03.06.2020).
- Курс доллара к евро. URL: https://finance.rambler.ru/currencies/kross-kurs/ (дата обращения: 03.06.2020).
- Отчет по счету туризма. Экономические и туристический последствия туризма 20162017. URL: https://www.businessfinland.fi/499c03/conte ntassets/4b07e 15186484a69b62e991 ed85a6c 45/matkailutilinpito_2016-2017.pdf (дата обращения: 16.06.2020).
- Янченко Т.В., Затонский А.В. Определение оптимальной ранжировки частных критериев оценки краевого социального ресурса // Экономика и менеджмент систем управления. 2013. № 4 (10). С. 99-104.


