Прогнозирование количества преступлений в Российской Федерации с помощью нейрона

Автор: Кайбичев И.А., Семенов В.А.

Журнал: Вестник экономики, управления и права @vestnik-urep

Статья в выпуске: 2 (51), 2020 года.

Бесплатный доступ

Предпринята попытка прогноза количества преступлений в Российской Федерации с помощью нейрона. Сравнение реальных и прогнозных значений за период 2004 2019 годов приводит к выводу о достаточно хорошем качестве прогноза. Величина относительной ошибки находилась в интервале от 0,18 до 15,49%.

Количество преступлений, математическое прогнозирование, нейронная сеть

Короткий адрес: https://sciup.org/142226838

IDR: 142226838

Текст научной статьи Прогнозирование количества преступлений в Российской Федерации с помощью нейрона

Одной из важных задач в работе правоохранительных органов является анализ состояния и прогнозирования преступности [1-6]. Прогноз основан на выделении статистических данных тренда и продления его будущего [7].

Авторегрессионные модели прогнозирования числа убийств в городах США предложены в работе [8]. Методы временных рядов [9-11] для предсказания преступности применены в исследовании [3].

Разбегаев [12] на основе анализа о динамике преступности в России с 1976 по 2006 годы получил уравнение для количества зарегистрированных преступлений

Y t = 880,23 * exp 0,0497(t - 1976) (1)

где Y(t) - число зарегистрированных преступлений, t - номер года (время). Аналогичная модель была использована для описания количества преступлений в Волгоградской области.

В последние годы стали популярен про-

* *

гноз показателей преступности с помощью нейронных сетей [13]. Применим этот подход для прогнозирования количества преступлений в Российской Федерации.

Математический нейрон - это математическая модель биологического нейрона мозга [14]. Его изображают в виде кружочка со стрелками, обозначающими входы и выход. Мы в нашем исследовании используем упрощенный математический нейрон, имеющий два входа и один выход (Рис. 1).

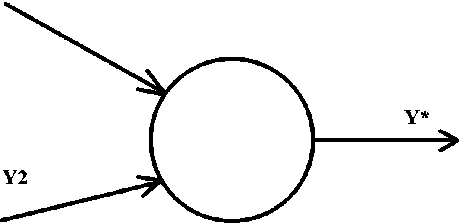
Рис. 1. Математический нейрон

Через вход математический нейрон принимает входные сигналы Y1 и Y2, которые суммирует, умножая каждый входной сигнал на некоторый весовой коэффициент Wj:

S=W1Y1 + W2Y2 (1)

Затем математический нейрон формирует свой выходной сигнал согласно:

Y = 1, если S>0

0, если S<0

в котором величину 0 называют порогом чувствительности нейрона.

Таким образом, математический нейрон существует в двух состояниях.

Если взвешенная сумма входных сигналов S меньше 0 , то его выходной сигнал Y равен нулю. В этом случае говорят, что нейрон не возбужден. Если же выходные сигналы достаточно интенсивны и их взвешенная сумма достигает порога чувствительности 0 , то нейрон переходит в возбужденное состояние, и на его выходе образуется сигнал Y = 1.

Весовые коэффициенты Wj имитируют электропроводность нервных волокон, силу синоптических связей между нейронами. Чем эти силы выше, тем больше вероятность перехода нейрона в возбужденное состояние при уменьшении порога чувствительности 0.

В нашем исследовании мы применим нейрон для прогнозирования количества преступлений в Российской Федерации. При этом моделирование работы мозга не требуется. На два входа нейрона мы будем подавать количество преступлений за прошедший и позапрошлый год, на выходе получать прогнозное значение на текущий год. При этом выходной сигнал должен быть некоторым числом, а не логическим значением. Данные по количеству преступлений за 2001-2019 года показывают, что ситуации, когда преступления отсутствуют, не было (Табл. 1).

Поэтому вместо нелинейной функции активации нейрона (2) проще использовать линейную функцию

Y* = S (3)

После создания нейронной сети начинается этап обучения. В процессе обучения нужно определить значения весовых коэффициентов W1 и W2 в формуле (1). Состояние обучения нейрона возникает при подаче на входы Y1 и Y2 данных за два предыдущих года, а на выход Y* - данных за текущий год. При этом данные за текущий год

Количество преступлений в Российской Федерации

Таблица 1

Год

2001

2002

2003

2004

2005

2006

2007

2008

2009

(тыс.)

2968,3

2526,3

2756,4

2893,8

3554,7

3855,4

3582,5

3209,9

2994,8

Год

2010

2011

2012

2013

2014

2015

2016

2017

2018

(тыс.)

2628,8

2404,8

2302,2

2206,2

2190,6

2388,5

2160,1

2058,5

1991,5

Год 2019 Y (тыс.) 2024,3 являются тестовыми. Весовые коэффициенты W1 и W2 в формуле (1) нужно подобрать так, чтобы получить результат, совпадающий с тестовым.

Для имитации процесса обучения использовали средство “Поиск решения” программы Microsoft Excel. Для подсчета весовых коэффициентов W1 и W2 брали начальные значения 1 и с помощью сервиса “Поиск решений” находили нужные значения.

В базу обучения для прогноза на 2004 год входят 2001 и 2002 гг. Данные 2003 г. используются в качестве эталона (Табл. 2).

Таблица 2

Этап обучения нейрона

Год	Y(тыс.)	w1	w2	Y*
2001	2968,3	0,465	0,5447	2756,4
2002	2526,3
2003	2756,4

После обучения нейрона весовые коэффициенты W1и W2 запоминали.

На этапе прогнозирования на входы ней- рона подавали 2002 и 2003 гг. (Табл. 3). На выходе Y* получали прогнозное значение на 2004 год.

Таблица 3

Этап прогнозирования

Год	Y(тыс.)	w1	w2	Y*
2002	2526,3	0,465	0,5447	2676,2
2003	2756,4
2004	2893,8

Ошибка прогнозирования равна e = Y*-Y. Для 2004 года е = - 217,6.

Модуль относительной ошибки составил

£ = Л = 7,52 % (4)

При прогнозировании на 2005 год процедура меняется. В процессе обучения используем данные 2002и 2003 годов, тестовым значением были данные 2004 года. Для прогноза используем данные 2003 и 2004 годов. В результате нейрон выдал прогнозное значение на 2005 год 3803,5 тыс. (Табл. 4). Модуль относительной ошибки составил 7 %.

Таблица 4

Год	W 1	W 2	Y (тыс.)	Y*(тыс.)	e	£
2004	0,46503	0,544691	2893,8	2676,2	-217,6	7,52%
2005	0,687734	0,659292	3554,7	3803,5	248,8	7,00%
2006	0,690255	0,674815	3855,4	4396,2	540,8	14,03%
2007	0,605253	0,515098	3582,5	4137,4	554,9	15,49%
2008	0,457075	0,411147	3209,9	3235,1	25,2	0,79%
2009	0,381555	0,425331	2994,8	2732,2	-262,6	8,77%
2010	0,355334	0,422383	2628,8	2405,5	-223,3	8,49%
2011	0,367107	0,409518	2404,8	2176,0	-228,8	9,52%
2012	0,373596	0,45015	2302,2	2064 6	-237,6	10,32%
2013	0,414477	0,46437	2206,2	2065,8	-140,4	6,36%
2014	0,453997	0,477292	2190,6	2098,2	-92,4	4,22%
2015	0,519994	0,54001	2388,5	2330,2	-58,3	2,44%
2016	0,48949	0,493099	2160,1	2250,0	89,9	4,16%
2017	0,474313	0,426822	2058,5	2054,9	-3,6	0,18%
2018	0,411082	0,467397	1991,5	1850,1	-141,4	7,10%
2019	0,467632	0,492672	2024,3	1943,8	-80,5	3,98%
2020	0,508235	0,491691		2025,4

Результаты прогноза

Прогнозное значение на 2020 год составило 2025,4 тыс. (Табл. 4).

Поскольку фактических данных пока нет, ошибку мы найти не можем.

Сравнение реальных и прогнозных значений (Рис. 1) приводит к выводу о достаточно хорошем качестве прогноза. Величина относительной ошибки находи- лась в интервале от 0,18 до 15,49 %.

Метод прогнозирования с помощью нейрона достаточно прост и не требует сложной математики. На примере данных по количеству преступлений в Российской Федерации за 2004-2019 годы установлено, что величина относительной ошибки прогноза находилась в интервале от 0,18 до 15,49%.

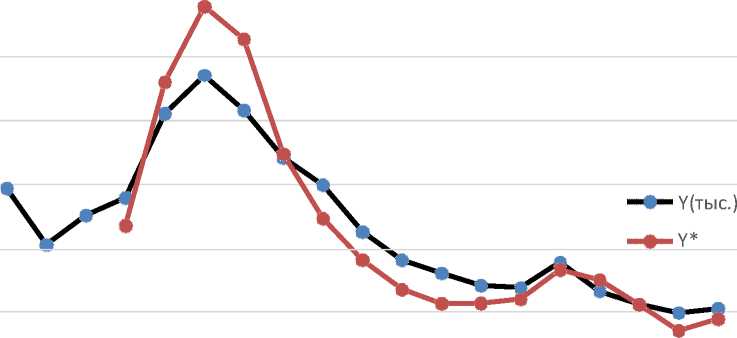
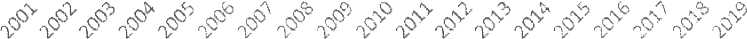
Рис. 2. Сравнение фактических и прогнозных значений

Список литературы Прогнозирование количества преступлений в Российской Федерации с помощью нейрона

Состояние преступности в России за январь - декабрь 2019 г. М.: Главное управление правовой статистики и информационных технологий Генеральной прокуратуры Российской Федерации, 2019. 52 с.
Schneider S. Predicting crime: a review ofthe research. Department of Justice of Canada, Research and Statistics Division, 2002. 37 p.
Henderson M.T., Wolfers J., Zitzewitz E. Predicting crime // John M. Olin Program in Law and Economics Working Paper No. 402. Chicago: The Law Scholl The University of Chicago, 2008. 63 p.
Омигов В.И. Прогноз преступности как эффективное средство противодействия преступности // Юридические записки. 2014. № 1. С. 9 - 14.
Разбегаев П.В. Состояние преступности в Волгоградской области как критерий формирования прогноза в регионе // Теория и практика общественного развития. 2014. № 18. С. 102 - 103.
Разбегаев П.В. Прогноз преступности в Волгоградской области: комплексный подход // Теория и практика общественного развития. 2015. № 20. С. 127 - 129.
Галкин Д.В. Анализ и прогноз отдельных видов преступлений, подследственных СК России, по итогам 2017 года: аналитический обзор. Хабаровск: пятый факультет Московской академии СК России, 2018. 26 с.
Peper John V. Forecasting crime: A city level analysis. ResearchGate. 2007. 33p. URL:https:/ /www.researchgate.net/publication /228655293_Forecasting_ crime_A_city-level_analysis
Box G.E.P., Jenkins G.M., Reinsel G.C., Ljung G.M. Time Series Analysis: Forecasting and Control. N.Y.: John Wiley and Sons, 2015. 712 p.
Shumway R., Stoffer D.S. Time Series Analysis and its Applications. Springer, 2000. 549 p.
Tsay R.S. Analysis offinancial time series. N.Y.: Wiley, 2010. 715 p.
Разбегаев П.В. Подходы к прогнозированию преступности в Волгоградской области: экстраполяция динамических рядов // Теория и практика общественного развития. 2015. № 19. С. 89 - 91.
Вахрушев А.А. Прогнозирование уровня преступности на основе статистических данных: Магистерская диссертация. СПб.: Санкт- Петербургский государственный университет, 2016. 37 с.
Комарцова Л.Г., Максимов А.В. Нейрокомпьютеры. М.: МГТУ им. Н.Э. Баумана, 2004. 400 с.

Еще

Статья научная