Rainfall Events Evaluation Using Adaptive Neural-Fuzzy Inference System

Published Online August 2014 in MECS

The meteorological phenomenon selected here to show Adaptive Neural-Fuzzy Inference System (ANFIS) method is rainfall events. Information on rain forecast is vital in agricultural areas specifically at the northeast of Iran where many crops irrigation primarily on the rain water, so an expert system models based on ANFIS will be introduced to forecast rainfall in Mashhad city (see Fig. 1).

For the area under research, statistical and synoptic studies prove that the chance of rain in winter and spring is more than in autumn. Rainfall forecast is a necessary and important process these days; annually lots of people has died and displaced by rains and floods. Different models can be used for rainfall prediction. Arnaud et al. introduced a rainfall model on the assumption that the process under investigation is a stationary one and it is according to the use of independent variables describing rainfall events [1].

Manel et al. studied rainfall changes in southern Tunisia by examining monthly and annual rainfall data [2]. Charabi and Al Hatrushi has been investigated the relationship between winter rainfall in Oman and the large-scale circulation and synoptic activity monthly [3]. Bookhagen discussed about the appearance of extreme monsoonal rainfall events in the Himalaya [4]. Melani et al. has been used various satellite images to study rainfall changes related to the summer African from April to October [5].

Fig. 1. Mashhad city on the Iran’s map

Weather forecasting has considered as one of the most important and demanding operational responsibilities accomplished by meteorological services all over the globe. It is a complex process that consists of many specialized fields of know- how [6]. Since in the field of meteorology all decisions must be taken in the uncertainty, the task is complex.

Many other authors have studied the uncertainty related to the weather systems [7], [8]. Also, the attention of modern scientists such as Sivakumar, Sivakumar et al., Men et al., have attracted to chaotic feature related to the atmospheric events [9], [10], [11]. Different scientists have developed some statistical models such as stochastic weather models that can be used as random number generators whose output are similar to the weather data [12]. In most cases, statistical models have the drawback that depends upon unspoken assumptions concerning the system. But, a chaotic system such as atmosphere cannot be bound by any hypothesis. However, lots of investigations have shown that NWP models are subject to errors and biases since the complicated atmospheric uncertainties and limited knowledge of the mathematical formulation of the atmospheric physics and dynamics [13].

The numerical models are according to the scheme of nonlinear operator equations which exist in the atmospheric system. The only method when there is not any analog solution of this system of operator equations is numerical solution based on various assumptions. Additionally, the chaotic behaviors of these nonlinear equations are sensitive to basic equations that make it more complicated to solve these equations [6]. Finally, perfect forecast comes out.

Artificial intelligence has been later studied in weather forecasting. The ability of adaptive neural-fuzzy inference system (ANFIS) to control inexact and contradictory real-world data made it appropriate for different kinds of application.

Artificial Intelligence (AI) refers to the ability of a machine to accomplish tasks and functions, resemble them to those that portray human’s thought. The term AI has been used to computer systems and programs that can do tasks which are more complicated than straight forward programming. Artificial intelligence includes several branches like Expert Systems (ESs), Artificial Neural Networks (ANNs), Adaptive Neural-Fuzzy Inference System (ANFIS), Genetic Algorithms (GA) and Fuzzy Logic (FL) and different Hybrid Systems (HS), which are combination of two or more of the branches mentioned previously [14]. In order to producing powerful computing systems, artificial intelligence technologies have a natural effectiveness that can be exploited.

Sometimes, the main purpose is to produce better and more efficient computing systems. Furthermore, artificial intelligence has been utilized for optimization, identification, prediction, modeling, forecasting, and control of complex systems [15]. For applying this, some features related to human intelligence like learning and the ability to insert from current knowledge must be considered. In order to achieving to useful systems with improvement in performance or other features, the suitable use of intelligent technologies is vital [8].

Fuzzy logic is an approach can deal with ambiguity that often happened in cases associated with meteorological forecast fields. The basic structure of a fuzzy inference system is a model that maps input characteristics to input membership functions, input membership function to rules, rules to a set of output characteristics, output characteristics to output membership functions, and the output membership function to a single-valued output or a decision associated with the output. You have considered only fixed membership functions that were chosen arbitrarily. You have applied fuzzy inference to only modeling systems whose rule structure is essentially predetermined by the user’s interpretation of the characteristics of the variables in the model.

ANFIS applies fuzzy inference techniques to data modeling. As you have seen from the other fuzzy inference GUIs, the shape of the membership functions depends on parameters. Therefore, changing these parameters can change the shape of membership function. Instead of looking at the data for choosing membership function parameters, membership function parameters using these fuzzy logic applications must be chosen automatically. Generally, the field of meteorology includes a system of concepts, methods, and principals for handling the modes of reasoning that are rough rather than exact.

The great potential for weather forecast can be achieved of the capability of handling imprecision. In the recent years, fuzzy techniques play an important role for handling this kind of complicated and non-linear problems. The technique has been used to many meteorological challenges such as climate classification [16], classification of atmospheric circulation pattern [17], long term rainfall forecasting [18], forecasting of temperature- humidity index using fuzzy logic approach [19] and fog forecasting using rule based fuzzy inference system [20].

One of the most complicated elements in such fields is rainfall forecasting because rainfall is a kind of process that is related to some precursors from other parameters like the surface pressure for weekly to longer than daily time scale, sea surface temperature for monthly to seasonal time scales and other atmospheric parameters for daily to hourly time scales. The other atmospheric parameters include temperature, relative humidity, dew point and wind.

The main factors in precipitation event could be the variability of weather especially those atmospheric parameters mentioned previously. Rainfall prediction is much more possible when a variability pattern for future trajectory could be recognized. Shao has applied fuzzy logic for cloud amount, cloud type, wind speed and relative humidity to compose a fuzzy function of weather categorization for thermal mapping [21].

Hansen has used fuzzy K-NN weather forecasting system to improve the technique of persistence climatology by using past and present cases [22]. A neural-fuzzy system for modeling wet season tropical rainfall has been used [23]. Fallah-Ghalhary et al. has used fuzzy inference system in the northeast of Iran for forecasting rainfall time series based on the rainfall data [24].

In this study, adaptive neural-fuzzy inference system has been applied to evaluate rainfall events for every given hourly data for a station in Mashhad by generating membership functions for each input parameter (relative humidity, total cloud cover, dew point temperature, surface pressure and temperature) and output gives nonrain fall or rainfall event.

• II.    Fuzzy Inference Systems

Fuzzy inference systems are known as fuzzy-rule based systems, fuzzy models, fuzzy associative memories, or fuzzy controllers when used as controllers. Basically a fuzzy interference system is composed of five functional blocks:

• 1)    A rule base containing a number of fuzzy if-then rules;

• 2)    A database which defines the membership functions of the fuzzy sets used in the fuzzy rules;

• 3)    A decision-making unit which performs the inference operations on the rules;

• 4)    A fuzzification interface which transforms the crisp inputs into degree of match with linguistic values;

• 5)    A defuzzification interface which transforms the fuzzy results of the inference into a crisp output.

Usually, the rule base and data base are jointly referred to as the knowledge base. The steps of fuzzy reasoning (inference operations fuzzy if- then rules) performed by fuzzy inference systems are:

• 1)    Compare the input variables with the membership functions on the premise part to obtain the membership values (or compatibility measures) of each linguistic label. (This step is often called fuzzification).

• 2)    Combine (though a specific T-norm or S-term operator) the membership values on the premise part to get firing strength (weight) of each rule.

• 3)    Generate the qualified consequent (either fuzzy or crisp) of each rule depending on the firing strength.

• 4)    Aggregate the qualified consequents to produce a crisp output. (This step is called defuzzification). Several types of fuzzy reasoning have been proposed in the literature [25].

Depending on the types of fuzzy reasoning and fuzzy if-then rules employed, most fuzzy inference systems can be classified into three types:

Type 1: the overall output is the weighted average of each rule’s crisp output induced by the ruler’s firing strength (the product or minimum of the degrees of match with the premise part) and output membership functions. The output membership functions used in this scheme must be monotonic functions [26].

Type 2: the overall fuzzy output is derived by applying “max” operator to the qualified fuzzy outputs (each of which is equal to the minimum of firing strength and the output membership function of each rule). Various schemes have been proposed to choose the final crisp output based on the overall fuzzy output, some of them are centroid of area, bisector of area , mean of maxima, maximum criterion [25].

Type3: Takagi and Sugeno’s fuzzy if- then rules are used [27]. The output of each rule is a linear combination of input variables plus a constant term, and the final output is the weighted average of each rule’s output.

• III.    Adaptive Neural-Fuzzy Inference Systems

Our attempt is to forecast rainfall with the help of fuzzy logic based approximate reasoning. This process uses the concept of an ANFIS which is in fact a superset of all kinds of feed forward neural networks with supervised learning capability. An adaptive network (See Fig. 2), as its name implies, is a network structure consisting of needs a directional links through which the nodes are connected. Part or all of the nodes are adaptive, which means their outputs depend on the parameter(s) pertaining to these nodes, and the learning rules specifies how these parameters should be changed to minimize a prescribed error measure.

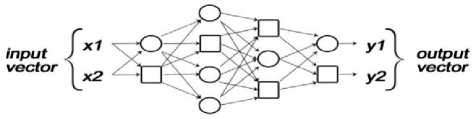
Fig. 2. An adaptive network.

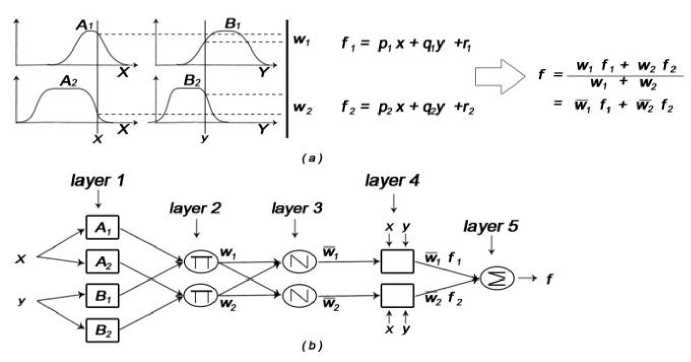
Fig. 3. (a) Type-3 fuzzy reasoning (b) equivalent ANFIS [28]

The type 3 fuzzy reasoning has been illustrated in figure 3(a) and the corresponding equivalent ANFIS architecture (type-3 ANFIS) is shown in Figure 4(b). The node function in the same layer is of same function family. Every nod in the first layer is a square node with a node function.

O i = M a. ( x ) (1)

where x is the input to node i, and Ai is the linguistic label (small, large, etc.) associated with this node function. In other word, Oi1 is the membership function of Aj and it specifies the quantifier Ai. Usually ^t (X) has been chosen to be bell- shaped with maximum equal to 1 and minimum equal to 0, Such as Equation 2 or 3

layer. Parameters in this layer are referred to as premise

parameters.

The single node in the last layer is a circle node

^Ai( x) =

1 + ( x - c) )² b a_i

labeled ^

computes the overall output as the

summation of all incoming signals, i.e.

O 5 = S Wifi

X - C 2\

M ai ⁽ x ) = exP⁽ -⁽----- ) )                     (3)

ai

Where {ai, bi, ci} is the parameter set. As the values of these parameters change, the bell- shaped function is on linguistic label Ai. In fact, any continuous and piecewise differentiable functions, such as commonly used trapezoidal or triangular- shaped membership functions, are also qualified candidates for node functions in this

Thus, we have constructed an adaptive network which is functionally equivalent to a type 4 fuzzy inference system. For type 1 fuzzy inference system, the extension is quite straightforward and the output membership function is the firing strength. For type 2 fuzzy inference systems, if we replace the centroid deffuzification centroid of area, then type 3 ANFIS can be constructed. However, it will be more complicated than its type 3 and type 1 versions and thus not worth the efforts to do so.

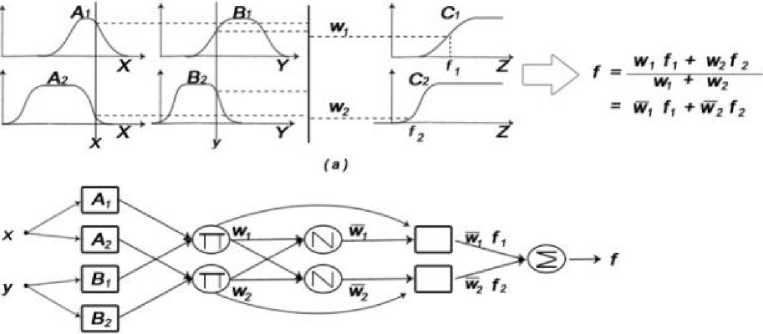
(b)

Fig. 4. (a) Type 1 fuzzy reasoning (b) Equivalent ANFIS [28]

As mentioned earlier, the seasonal rainfall forecast using fuzzy-neural networks was carried out for the first 5 months of 2007 to 2012. The rainfall data was obtained from the National Meteorological Agency. The membership functions and their IF-THEN rules were defined in MATLAB software using artificial neural-fuzzy inference system.

Four input variables of temperature, due point, humidity and total cloud cover (cloudiness) were considered for the system as they had the most influence on the climate and the rainfall in a region. Another output variable was also considered for the system with each of these variables including 121 membership functions. The specified range for each variable was as follows: humidity (0 to100), total cloud cover (0 to 8), temperature (-15 to 33 C) and due point (-18 to18 C).

It can be classified into three different phase: loading data, the rule base and training and testing data. In loading data phase, the data related to the past annual rainfalls are loaded into ANFIS system in order to help forecast the rainfalls. The rule base is a set of rules of the IF-THEN form. The IF portion of a rule refers to the degree of membership in one of fuzzy sets. The THEN portion refers to the consequences, or the associated system output fuzzy set. We edit the rules using ANFIS rule editor and testing against checking data set.

For generating FIS, subtractive clustering method has been considered. For editing rules using ANFIS, there are four parameters that play the most important role range of influence, squash factor, accept Ratio and reject ratio. Range of influence represents the degree of influence for each of membership functions (0-100), that is the overlapping of two membership functions. Squash factor shows the shape of membership functions, and accept ratio and reject ratio represent the ratio with which the data are accepted or rejected. According to the experiments, the practical values for each of these factors are range of Influence = 0.13, squash factor = 1.15, accept ratio = 0.5 and reject ratio = 0.15.

By applying these values, we will develop 121 membership functions and rules for each of the inputs, which are generated by the ANFIS automatically. The properties for the sets of rules are completeness, consistency, continuity and interaction. A set of IF-THEN rules is complete if any combination of input values result in a suitable output value. A set of IF-THEN rules is inconsistent if there are two rules with the same rules- antecedent but different rule- consequents. A set of

IF-THEN rules is continuous if it does not have neighboring rules with output fuzzy sets that have empty intersection. In the interaction property, suppose that is a rule, “IF x is A THEN y is B”, this meaning is represented by a fuzzy relation R, and then the composition of A and R does not deliver.

в = ⃘ R

B is inferred from A using relation matrix R which defines the mapping between x and y and the operation ‘ᵒ’ is defined as the max-min operation.

Examples from the rules we edit are:

• a.    If (in1 is in1 cluster 1) and (in2 is in2 cluster1) and (in3 is in in3 cluster1) and (in 4 is in4 cluster1) then (out1 is out1 cluster1)

• b.    If (in1 is in1 cluster2) and (in2 is in2 cluster2) and (in3 is in3 cluster2) and (in4 is in4 cluster2) then (out1 is out1 cluster2).

in1, in2, in3 and in4 are input data, whereas out1 and out2 are output data.

Some data need to be trained based on the loaded data and IF-THEN rules. By comparing the obtained values with the real values, the error of ANFIS system is achieved, which should be minimized.

• IV.    Discussion

  We managed to evaluate the rainfall and non-rainfall events in terms of 0 (non-rainfall) and 1 (rainfall) through a set of different experiments. After simulating ANFIS system, the error value was equal to 0.13043 of 1053 data used in the system; only 100 data were different from their real values. The error of system could be reduced by increasing the number of system inputs or using larger number of experiment data. The study data included temperature, due point, total cloud cover and humidity, which had been used over the years 2007-2012 for the months of January to June. The output percentage was approximately 90.5%, which can be considered as a successful evaluation. However, there are still some degrees of uncertainty associated with the models output to evaluate the rainfall. Sample of input data and its result has been shown in Tab. 1. The last column of the table illustrates differences between real rainfall and evaluated rainfall.

Table 1. Input Data and Results

Temperature	Due point	Cloudiness	Humidity	Real rainfall	ANFIS Output	Real rainfall (0 or 1)	ANFIS Output (0 or 1)	Comparison	Error
-3.375	-5.6625	3.125	85.25	0	0.061413	0	0	0	100
-3.775	-5.4625	6.375	88.375	0	0.433292	0	1	1
-4.925	-8.3875	2	77.125	0	-0.06894	0	0	0
-3.425	-9.05	0	66.875	0	0.003142	0	0	0
-1.625	-7.425	0.75	66.25	0	-0.03383	0	0	0
0.425	-4.175	5.375	71.875	0	-0.21339	0	0	0
2.625	-3.4625	2.375	65.5	0	0.029641	0	0	0
0.775	-0.35	7.625	92.5	0.6	0.934837	1	1	0
0.575	-0.35	4.75	93.875	0	0.115366	0	0	0
1.35	-1.9375	2.25	80.125	0	-0.02391	0	0	0
0.85	-2.4875	2	78.875	0	0.002521	0	0	0
0.45	-4.5875	0.125	70.875	0	-0.09274	0	0	0
1.425	-3.525	4.25	70.5	0	0.10153	0	0	0
4.7	-1.375	1.875	65.625	0	0.100873	0	0	0
3.05	-1.15	3.625	74.25	0	-0.03754	0	0	0

• V.    Conclusion

In this paper, intelligent models based on adaptive neural-fuzzy inference system have been introduced for rainfall events evaluation for Mashhad meteorological station. It is proven that when using such technique, it is desirable to merge the experiences of forecasters and theoretical studies with efficiency and the accuracy of the computer systems by procedure based on algorithm. In this algorithm, the appropriate clusters for generating fuzzy rules have been defined. After implementing the model, achieved results show a high agreement with the actual data. The models presented can be improved by increasing the set of input parameters; adjusting the set of rules to get multiple weather phenomena forecast e.g. and/or wind direction. The error consideration mainly responsible for the accuracy and experience of the one who puts the length at training data set.