Разработка математической модели формирования компетенций для реализации интеллектуального поиска средствами Matlab

Семантический анализ является непростой математической задачей, несмотря на то что он востребован практически во всех областях жизни человека. Сложность состоит в обучении компьютера правильно распознавать и трактовать образы, которые пользователь пытается передать. Т. Гонсалес полагает, что человек представляет собой очень сложную информационную систему - в определенной степени это определяется чрезвычайно развитыми у него способностями распознавать образы. Образ - это описание объекта. Естественный язык образовывался во многом хаотично в отличие от алгоритмических языков. По этой причине возникает целый ряд сложностей в понимании и распознавании текста [1, с. 4]. Так, для разработки программы, которая будет давать возможность интеллектуального поиска бизнес-кейсов, деловых игр, необходимо разработать математическую модель принятия решений, направленных на облегченный поиск заданий для развития компетенций личности.

Моделирование формирования компетенций в динамической среде

Управление формированием компетенций невозможно считать эффективным без рассмотрения их в контексте математической модели. При сопоставлении полученных результатов с ожидаемыми формируется действенная система мер, а также происходит оценка результативности. В основе разработанной модели лежит следующее утверждение: формирование компетенций личности происходит исключительно в процессе целенаправленной деятельности. Следовательно, процесс формирования компетенций можно считать динамическим.

Из базовых положений теории оптимального управления процессами следует, что математическая модель содержит такие компоненты, как дифференциальные связи, фазовые координаты, управления, ограничения, замыкание модели блоками принятия решений.

В данном исследовании фазовые координаты будут показывать уровень познания определенных компетенций и степень стремления обучаемого к повышению его компетентности в целом. Пусть t - время, дни от момента начала обучения; n - количество определенных компетенций; X i ( t ) - степень компетентности личности по направлению i в момент t; M(t) - степень стремления обучаемого к деятельности, приводящей к повышению ее компетентности. Примем степень компетентности относительной величиной, которая варьирует в промежутке [0; 1]. При степени компетентности, равной нулю, можно считать, что обучаемый к моменту получения заданий обладает абсолютной некомпетентностью, при единице возникает абсолютное достижение максимально возможного уровня компетентности [2, с. 39]:

0 <  x(t ) < 1, i = 1, .... n .

Введем X , которая оценивает в целом компетентность личности. Следуя теории многокритериальной оптимизации (свертка оценки по различным направлениям компетентности в единое число), получим:

X(t)  ^Lc x (t)’ i=1

где весовые коэффициенты c c,*0, Lc = 1

i =1

показывают относительную ценность различных направлений компетентности в профиле подготовки специалиста.

Уровень активности личности ^{M (} t ) будем измерять в час/день.

Перейдем к описанию управлений.

Если принять за k количество видов заданий, которые развивают ту или иную компетенцию, а за m j (t) - поиск занятий j -го вида деятельности в момент времени t , j = 1, ..., k , то получим степень стремления обучаемого к деятельности, приводящую к повышению определенной компетенции:

k

L mA t)=M(tу j=1

Как правило, скорость накопления навыков пропорциональна:

• 1)    интенсивности решения заданий, которые влияют на формирование компетентности;

• 2)    предрасположенности обучаемого к решению таких видов заданий, которые указаны в п. 1;

• 3)    достигнутому уровню компетентности;

• 4)    объему еще не освоенных обучаемым компонентов.

Необходимо учитывать, что влияние компетентности, которая была доступна, - равнонаправленное. Тем самым такую систему можно считать закономерной. Деятельность обучаемых не дискретна, имеет комплексный характер и не может быть избирательно направлена на какой-либо один элемент компетентности. Отсюда следует, что, с одной стороны, чем выше уровень навыков обучаемого, тем эффективнее деятельность развития компетенции и, соответственно, ее влияние на рост компетентности в целом. Но, с другой стороны, чем выше компетентность обучаемого, тем больше компетенций им уже освоено, а количество неосвоенных элементов целостной системы становится меньше, и их уже необходимо исключать из нее. Иначе говоря, практическая эффективность деятельности возрастает, а ее обучающая эффективность падает. Именно такое двунаправленное влияние текущей компетентности приводит к тому, что кривая роста компетентности в процессе деятельности носит S-образный характер, как показано на рисунке 1.

Проанализировав вышесказанное, можно прийти к системе обыкновенных дифференциальных уравнений:

dx      ^k

• ,  = ⁽ L ^в a mi)X ^{(1 -} X ) i = 1,..., n

^dt      j =1

где B j - коэффициент влияния j -го вида деятельности на формирование компетентности по i -му направлению.

Скорость изменения активности личности прямо пропорционально зависит от ее мотивации на развитие компетенции, содержания и результатов деятельности, их оценки обществом (стимулирования), а также ограничивается утомлением.

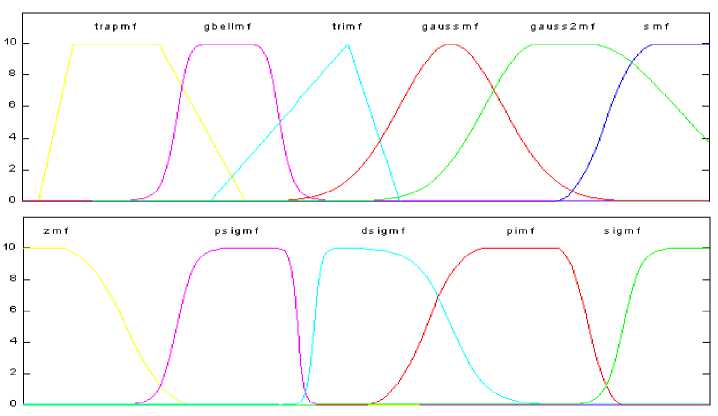
Рисунок 1 – Двунаправленное влияние текущей компетентности средствами Matlab

Вывод

Разработка математической модели формирования компетенций является важной частью реализации автоматизированной системы поиска заданий для развития компетенций. Помимо социального аспекта, необходимо учитывать математический аппарат, который дает понимание в реализации и систематизации заданий, необходимых обучаемому для развития той или иной компетенции – так же, как и создание семантического ядра невозможно без системы анализа данных, без основных аспектов принятия решений и математического моделирования реальных процессов.

Ссылки:

• 1.    Гонсалес Т.Дж. Принципы распознавания образов / пер. с англ. И.Б. Гуревича. М., 1978.

• 2.    Khaperskaya А.V., Slesarenko I.V. Fundamentals of course design training professional cycle discipline in English // Сборник материалов III Всероссийского научно-методологического семинара-конференции / под ред. Л.А. Сивицкой. Томск, 2016. 153 с.