Разработка методических рекомендаций для педагогов по интегральной оценке академической и интеллектуальной одаренности обучающихся

На сегодняшний день большинство зарубежных и отечественных психологов и педагогов считают приемлемым определение одаренности, сформулированное в 1972 г. Комитетом по образованию США, в котором указано, что талантливыми и одаренными детьми являются те дети, которые, по оценке опытных специалистов, в силу выдающихся способностей демонстрируют высокие достижения. Перспективы таких детей определяются уровнем их достижений и/или потенциальными возможностями в одной или нескольких сферах:

• 1)    академической (высокие показатели в школьном обучении);

• 2)    творческого или продуктивного мышления;

• 3)    художественной деятельности;

• 4)    общения и лидерства;

• 5)    интеллектуальной;

• 6)    экстрасенсорной;

• 7)    духовной;

• 8)    психомоторной;

• 9)    социальной.

Среди перечисленных видов одаренности в контексте данных исследований нас наиболее интересует академическая одаренность (АО), проявляющаяся, прежде всего, в умении учиться, то есть в успешности освоения отдельных учебных дисциплин, и являющаяся более избирательной, нежели интеллектуальная. Имеются в виду обучаемые, которые могут демонстрировать высокие результаты по легкости, глубине, быстроте освоения математики или иностранного языка, физики или биологии и иногда иметь неважную успеваемость по другим предметам, воспринимаемыми ими не так легко, и наоборот. То есть, речь идет о так называемых «физиках и лириках».

В данном контексте принципиально важным мы считаем обучение педагогов процедурам оценки в условиях применения объективного тестового контроля. Данное обучение осуществляется на базе Института одаренного ребенка НАПН Украины. Далее в статье мы подробнее остановимся на содержании обучения.

Принципиально важным моментом мы считаем обучение педагогов разработке надежных и простых процедур такой квалиметрии, результаты которой должны быть понятны всем участникам учебно-воспитательного процесса, в том числе и обучаемым.

В ходе обучения акцентируется внимание на то, что применение объективного тестового контроля предусматривает, прежде всего, наличие надежного и валидного теста. В этом случае уровень учебных достижений может быть измерен в абсолютной 100-балльной, а при проведении внешнего независимого оценивания - и 200балльной шкалах. Тогда результаты тестирования делают тривиальным ранжирование обучаемых по количественным уровням академической одаренности. Однако если количественному результату не придать качественной (вербальной, лингвистической) характеристики, то он может утратить свое мотивационное значение. Устранение этого замечания возможно путем построения функций принадлежности (ФП) лингвистической переменной (ЛП) «УУД», размерность терм-множества которой соответствует размерности принятой для оценки качественной шкалы, в качестве которой можно использовать и 4-балльную, и 7-балльную (европейскую «облегченную» ECTS), и 9балльную стенайнов, и 10-балльную стенов, и, конечно же, 12-балльную шкалы. Эти терм-множества, равно как и ФП, строятся методами теории нечетких множеств и ЛП. Общий вид этих функций иллюстрирует парадигма на рисунке 1 [1], где T n - обозначение терм-множества «УУД» (балльной шкалы оценок размерностью n ), T in - обозначение i -той оценки шкалы, i = 1,n .

Рисунки 2 и 3 иллюстрируют уже эмпирические функции принадлежности лингвистической переменной «уровня учебных достижений» для 4-балльной и 12-балльной шкал, полученные по результатам опроса репрезентативной выборки преподавателей вузов Украины на континууме 100-балльной шкалы. Точки на рисунках 2, 3 дают возможность анализировать представленные на них нечеткие модели на уровне квартилей и децилей, хотя возможен и более глубокий анализ на уровне процентилей, что особенно важно в случае необходимости сопоставить УУД в разных качественных шкалах.

Таким образом, в условиях объективного тестового контроля интегральная (обобщенная, агрегированная) оценка академической одаренности старшеклассника (которой и только которой присуще системное свойство эмерджент-ности [1; 2]) в пределах объема знаний отдельной учебной дисциплины устанавливается по его результатам с помощью нечетких моделей. С другой стороны, если тест предусматривает возможность оценивать уровень учебных дос -тижений по отдельным темам конкретной учебной дисциплины, либо, скажем, если речь идет уже об интеллектуальной одаренности (ИО), являющейся, безусловно, более общей по отношению к академической одаренности, то вроде бы явным является первоначальное тривиальное определение среднего показателя тестирования по всей совокупности изучаемых тем учебной дисциплины, либо по всей совокупности изучаемых учебных дисциплин:

1K

n = — е ni, (1) K i=1

где n i - результат тестирования по i -той теме учебной дисциплине (либо это интегральный показатель тестирования i -той учебной дисциплины, если речь идет об интеллектуальной одаренности), i = 1,K ; К - общее количество изучаемых учебных дисциплин или соответствующих тем внутри учебной дисциплины. Далее, обращаясь к рис. 2, 3, несложно перейти к качественной оценке УУД обучаемого, мотивирующей его на овладение знаниями. Таким образом, обеспечивается смешанное количественно-качественное измерение академической одаренности либо интеллектуальной одаренности.

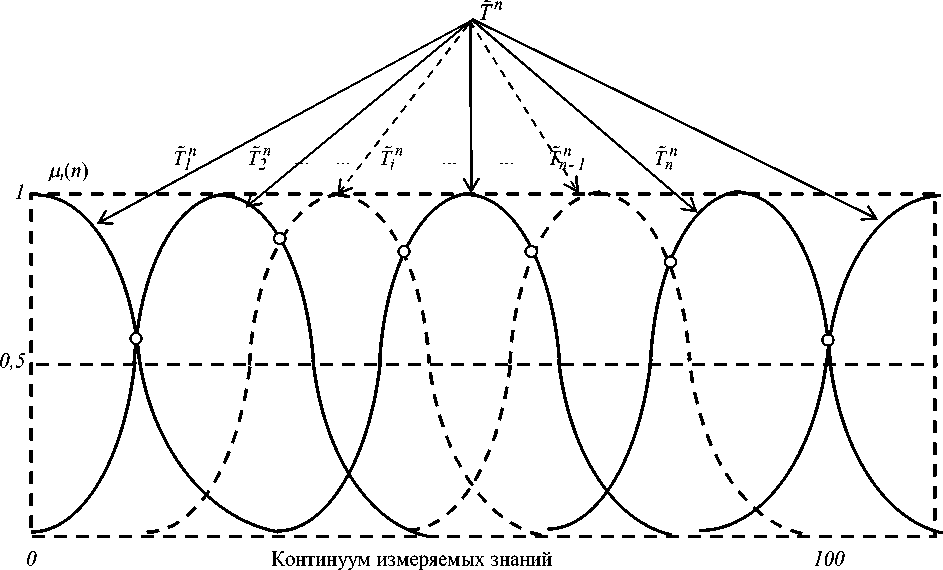
Рис. 1. Парадигма функций принадлежности лингвистической переменной «уровень учебных достижений»

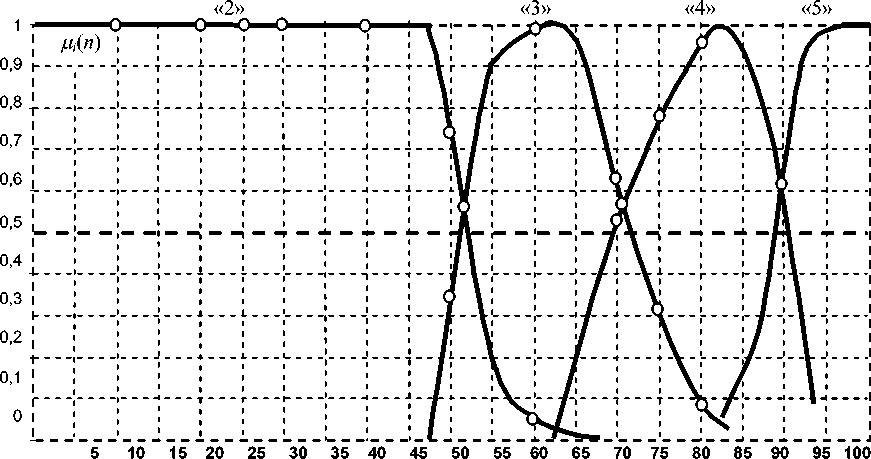
Континуум 100-балльной шкалы

Рис. 2. Эмпирические функции принадлежности лингвистической переменной «уровень учебных достижений» как нечеткой модели квалиметрии знаний в 4-балльной шкале на континууме 100-балльной

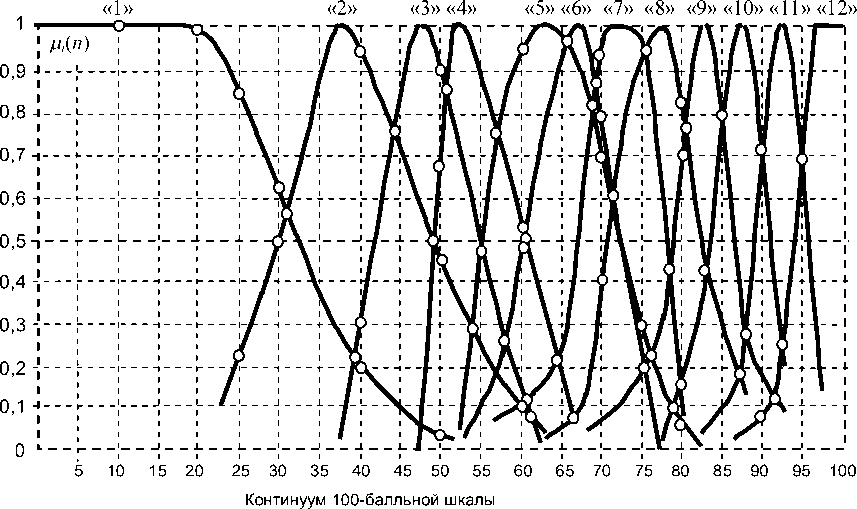
Рис. 3. Эмпирические функции принадлежности лингвистической переменной «уровень учебных достижений» как нечеткие модели квалиметрии знаний в 12-балльной шкале на континууме 100-балльной

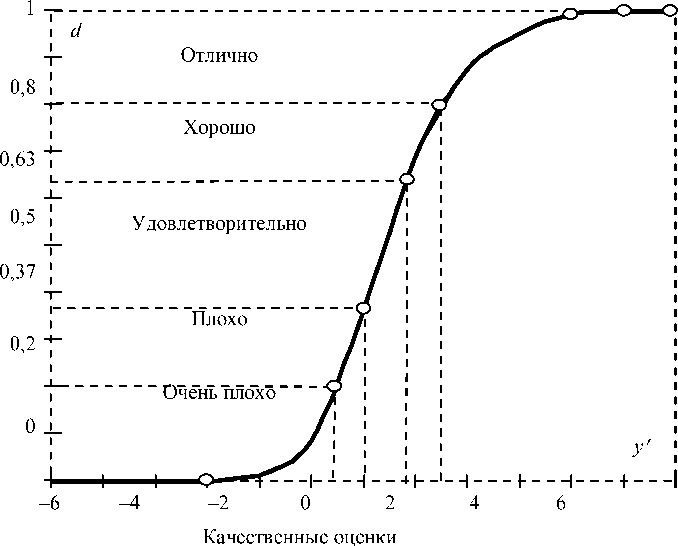
Рис. 4. Общий вид функции желательности Харрингтона

Отметим, что мы специально не ввели в формулу (1) весовые коэффициенты учебных дисциплин, поскольку интеллектуальная одаренность предусматривает глубокие знания обучаемых именно по всему разнообразному спектру изучаемых дисциплин, а не по их ограниченной направленности, что соответствовало бы изучению именно академической одаренности. При этом еще раз укажем, что только и только обобщенной (интегральной) оценке П присуще системное свойство эмерджентности, которого не имеет ни одна частная оценка академической одаренности n i .

В качестве замечания к рассмотренному подходу следует отнести следующее. Во-первых, требование к выравниванию надежности и валидности используемых тестов. Во-вторых, аддитивная функция агрегирования (1) по своей сути предполагает возможность абсолютной компенсации сколь угодно малых значений уровня учебных достижений сколь угодно большими, то есть в нее подспудно закладывается реальное существование «физиков и лириков». Скажем, неприемлемый результат «физика» n i =0 по i -той гуманитарной учебной дисциплине компенсируется абсолютной академической одаренности по j -той технической: n j =100.

Таким образом, рассмотренный аддитивный подход приемлем, если испытуемые получили по каждой изучаемой учебной дисциплине некоторую пусть минимальную, но позитивную «проходную» оценку.

В ходе обучения отмечается, что намного сложнее являются процедуры выявления интегрального показателя академической и интеллектуальной одаренностей при отсутствии объективного тестового контроля, поскольку в этом случае соответствующие оценки выставляются, только исходя из богатого, но все же субъективного опыта учебной работы экспертов-преподавателей. И обобщение этих оценок в интегральную по формуле (1) противоречило бы здравому смыслу, поскольку балльные оценки вышеперечисленных шкал (4-балльной, ... 12-балльной), исходя из положений теории измерений и методологии системного анализа [1-4], имеют явные характеристики шкал упорядочения (ранжирования). Это означает, что соответствующие оценки этих шкал только иллюстрируют сравнительную значимость глуби- ны и объема знаний, выявленных и оцененных преподавателем, но ни в коей мере не дают информации о количественных характеристиках этих знаний. Скажем, никак нельзя утверждать, что старшеклассник, получивший по какой-либо учебной дисциплине оценку «12», имеет в два раза больше знаний, чем его одноклассник с оценкой «6» (наилучший показатель 12балльной шкалы для лиц со «средним» (репродуктивным) уровнем учебных достижений). Именно поэтому никакие математические преобразования с этими оценками недопустимы.

Исходя из вышеизложенного, в условиях отсутствия объективного тестового контроля воз -никает задача перевода качественных оценок лингвистических шкал в количественные. Из анализа научных источников [1; 5-8] следует, что с этой целью можно было бы взять за основу либо функцию агрегирования «планирование по узкому месту», либо интегральную функцию желательности Харрингтона (Е. С. Harrington), опирающуюся на соответствующую шкалу (рис. 4).

В первом случае, когда не допускается никакая компенсация, интегральный показатель обученности определяется по наихудшему уровню учебных достижений. Такой подход чрезвычайно важен, скажем, при подготовке операторов особо сложных систем управления, профессиональная деятельность которых существенным образом влияет на безопасность этих систем. И именно такой подход был реализован для оценки точности пилотирования пилотов. Однако нам не известны случаи его применения в дидактике.

Во-втором случае применяется специальная шкала желательности результатов, которую относят к психофизиологическим вербально- (лин-гвистично)-численным шкалам. Назначение шкалы - установление связи между количественными физическими и психолого-педагогическими (качественными) параметрами.

Кривая на рисунке 4 была построена по результатам многочисленных наблюдений за исследователями и имеет такие полезные свойства, как непрерывность, монотонность и гладкость. Кроме того, эта кривая хорошо иллюстрирует тот факт, что в пределах желательности, приближенных к 0 или 1, «чувствительность» ее существенно ниже, чем в средней зоне. Однако этот тезис представляется нам несколько сомнительным, особенно в ракурсе вышеупомянутой деятельности операторов сложных систем управления, на уровень обученности которых накладываются ограничения не просто «проходной» по шкале, а «проходной» по высокому уровню учебных достижений оценке. И это, безусловно, существенно влияет на их мотивацию достижения высокого уровня учебных достижений и избегания низких уровней учебных достижений.

Изучаемая кривая на рисунке 4 описывается таким уравнением:

d = e e'y или d = exp { exp ( - y )} , (2) где exp - общепринятое обозначение экспоненты.

Уравнение (2) обеспечивает переход качественной оценки у_и в количественную d u : y_u Ю d_u . Имея значение частного отзыва (в нашем случае - отдельной качественной (лингвистической) оценки академической одаренности), несложно перейти в безразмерную шкалу ее желательности. При этом также несложно убедиться, что значение d_u=0 соответствует абсолютно неприемлемому результату обучения, а значение d_u=1 - наилучшему показателю академической одаренности.

Агрегированный (интегральный) показатель D был назван Харрингтоном обобщенной функцией желательности (ОФЖ) . Соответствующее обобщение, то есть переход d_u Ю D осуществляется согласно формуле:

n

D = n Х Х d u . (3) u =1

Как можно увидеть, обобщенная функция желательности задается как среднее геометрическое частных желательностей оценок, что соответствует мультипликативному подходу в решении одношаговых задач принятия решений с векторным показателем эффективности [1]. Такое представление можно рассматривать как удобную модель психологической реакции исследователя при решении задач определенного класса. Но при этом укажем, что, во-первых, обобщенная функция желательности весьма чувствительна к небольшим значениям частных желательностей. Во-вторых, как уже нами указывалось, представляется сомнительным небольшой прирост желательности высо- ких оценок (рис. 4), что в целом не соответствует мотивации на обучение, скажем, операторов особо сложных систем управления, существенным образом влияющих на безопасность этих систем. Однако, в-третьих, безусловным позитивом мультипликативного подхода (3) является возможность, в отличие от аддитивного подхода (1), относительной компенсации низких оценок одних показателей высокими оценками других. Оценка точности пилотирования, производимая, скажем, опираясь на методы выбросов случайных процессов , показывает его применимость в процессах профессиональной подготовки летного персонажа [9; 10].

Обобщенная функция желательности (3) является количественным, однозначным, единственным и универсальным показателем качества исследуемого объекта, а если прибавить еще и такие свойства, как адекватность, эффективность и статистическая чувствительность, то становится понятным, что ее действительно можно применять в качестве критерия оптимизации. Обобщенные функции желательности нашли широкое распространение в разнообразных отраслях, однако для решения педагогических проблем ее практически не применяют. Результаты наших исследований позволяют расширить спектр ее применимости в дидактике [8].

Рассматриваемая 5-балльная качественная шкала желательности, предложенная Харрингтоном, безусловно, не покрывает своими характеристиками все квалиметрические особенности и привлекательности других шкал, применяемых в дидактике. Тем более что объективные рекомендации по переходу из шкалы в шкалу возможны только при условии объек -тивного тестового контроля (что иллюстрируют, например, рис. 2, 3), случай отсутствия которого мы как раз и рассматриваем. Вместе с тем, представляется возможным усовершенствовать подход Харрингтона путем проведения иной, отличной от предложенной им процедуры дефаззификации оценок балльных шкал.

Речь о том, что под du в формуле (3) будем понимать количественную характеристику «желательности» (важности, приемлемости, значимости) балльной оценки уровня учебных достижений любой качественной шкалы, применяемой для квалиметрии академической одаренности (или интеллектуальной). Тогда, обобщая все частные количественные оценки, то есть находя их среднее геометрическое, несложно получить интегральную оценку академической одаренности обучаемого в рамках отдельной учебной дисциплины. Если же обобщить оценки по всей совокупности изучаемых дисциплин (например, оценки аттестата), то приходим к оценке интеллектуальной одаренности.

Рассмотрим общее содержание процедуры дефаззификации оценок на примере той же самой 5-балльной шкалы. Для нее тривиально такое ранжирование желательности соответствующих оценок:

~    ~     ~    ~     ~

T 5 f T 4 f T 3 f T 2 f T i ,       (4)

где T_i – у сл овное обозначение і- той оценки шкалы, i = 1,5 .

Ранжирование (4) можно также наглядно представить соответствующим графом приоритетности (желательности) оценок (рис. 5).

Далее, используя математический метод расстановки приоритетов, известный так же, как «задача про лидера» [11; 12], несложно вычислить коэффициенты важности (приоритетности, желательности, приемлемости) оценок 5-балльной шкалы с любой наперед заданной точностью (табл. 1).

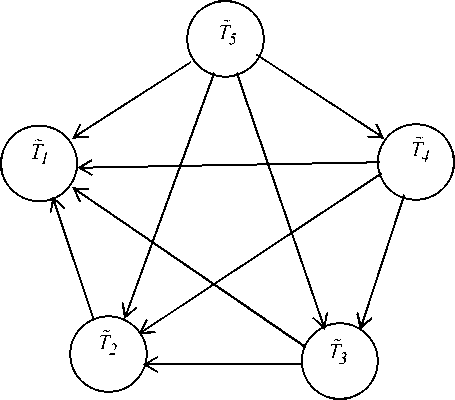
Рис. 5. Граф расстановки приоритетов (желательности) оценок 5-балльной шкалы

Таблица 1

— T i	Смежность оценок					Итерации
	— T 5	— T 4	— T 3	— T 2	— T 1	I		II		III		IV
						Σ c ij	a j	С j ( 2 )	a j ( 2 )	С j ( 3 )	a j ( 3 )	С j ( 4 )	a j ( 4 )
1	2	3	4	5	6	7	8	9	10	11	12	13	14
— T 5	1	2	2	2	2	9	0,36	41	0,4824	129	0,5734	321	0,6407
— T 4	0	1	2	2	2	7	0,28	25	0,2941	63	0,2800	129	0,2575
— T 3	0	0	1	2	2	5	0,20	13	0,1529	25	0,1111	41	0,0818
— T 2	0	0	0	1	2	3	0,12	5	0,0588	7	0,0311	9	0,0180
— T 1	0	0	0	0	1	1	0,04	1	0,0118	1	0,0044	1	0,0020
Σ						25	1	85	1	225	1	501	1

Продолжение таблицы 1

— T i	Итерации
	V		VI		VII		VIII		IX		Х
	С j ( 5 )	a j ( 5 )	С j ( 6 )	a j ( 6 )	С j ( 7 )	a j ( 7 )	С j ( 8 )	a j ( 8 )	С j ( 9 )	a j ( 9 )	С j ( 10 )	a j ( 10 )
15	16	17	18	19	20	21	22	23	24	25	26	27
— T 5	681	0,6914	1289	0,7258	2263	0,7488	3781	0,7685	6059	0,7875	9329	0,8053
— T 4	231	0,2345	377	0,2123	597	0,1976	921	0,1872	1357	0,1764	1913	0,1651
— T 3	61	0,0619	85	0,0479	135	0,0447	189	0,0384	247	0,0321	309	0,0267
— T 2	11	0,0112	24	0,0135	26	0,0086	28	0,0057	30	0,0039	32	0,0028
— T 1	1	0,0010	1	0,0006	1	0,0003	1	0,0002	1	0,0001	1	0,0001
Σ	985	1	1776	1	3022	1	4920	1	7694	1	11584	1

ПРИМЕЧАНИЕ:

С j ( k ) – ценность j- той оценки на k- той итерации; a j ( k ) – коэффициент желательности j- той оценки на k- той итерации

Коэффициенты значимости-желательности баллов наиболее известных оценочных шкал

Таблица 2

Балл / терм	Коэффициенты желательности-значимости оценок шкалы, α і
	4-балльной	5-балльной	7-балльной	9-балльной	10-балльной	12-балльной
1	2	3	4	5	6	7
1 / Т 1	–	0,0001	0,0001	0,0001	0,0001	0,0001
2 / Т 2	0,0001	0,0028	0,0009	0,0011	0,0006	0,0010
3 / Т 3	0,0048	0,0267	0,0059	0,0049	0,0029	0,0036
4 / Т 4	0,0825	0,1651	0,0260	0,0155	0,0092	0,0090
5 / Т 5	0,9126	0,8053	0,0895	0,0378	0,0229	0,0820
6 / Т 6			0,2536	0,0804	0,0486	0,0184
7 / Т 7			0,6240	0,1529	0,0921	0,0329
8 / Т 8				0,2668	0,1600	0,0546
9 / Т 9				0,4405	0,2606	0,1188
10 / Т 10					0,4030	0,1652
11 / Т 11						0,2226
12 / Т 12						0,2918
Σ	1	1	1	1	1	1

Матрица смежности оценок 5-балльной шкалы и итерации расстановки приоритетов на них

л«*««4.

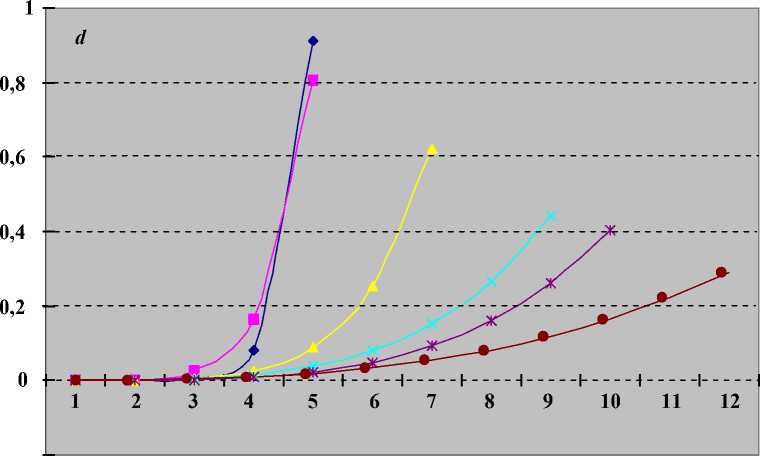
Рис. 6. Номограмма функций желательности основных балльных шкал

По аналогии с помощью того же самого метода расстановки приоритетов вычислены с точностью до четвертого знака после запятой и представлены для сравнительного анализа в таблице 2 коэффициенты желательности оценок рассматриваемых качественных шкал (4балльной, ..., 12-балльной).

Из анализа данных таблицы 2 вытекает более ярко выраженное в сравнении с рисунком 4 нелинейное соотношение наиболее и наименее желательных оценок исследуемых балльных шкал, что наглядно подтверждает рисунок 6.

Отмеченную нелинейность можно математически описать соответствующими экспонентами, что дает возможность применять для определения интегрального показателя академической одаренности (или интеллектуальной) аналитические методы:

– для 4-балльной шкалы:

d"4" =7Ч10–6e3,0201y(5)

– для 5-балльной шкалы:

d"5" =2Ч10–5 e2,2065y(6)

– для 7-балльной шкалы (ECTS):

dECTS =5Ч10–5e1,4363y(7)

– для 9-балльной шкалы стенайнов: d"9" =10–4e0,976y(8)

– для 10-балльной шкалы стенов:

d"10" =10–4e0,8785y(9)

– для 12-балльной шкалы:

d=4,1Ч10–4e0,6135y(10)

Таким образом, диапазон соответствующей «нормы» обобщенной функции желательности (3) будет определяться межбалльным количественным диапазоном, установленным либо по номограмме на рисунке 6, либо с помощью формул (6)–(10).

Отметим, что при применении метода расстановки приоритетов мы ориентировались только на одинаковую точность вычисления количественных коэффициентов желательности оценок. Поэтому, в силу специфики метода, высшая и низшая оценки шкалы в разы-порядки отличаются по «весу-желательности» от соседних, что особенно заметно для шкал небольшой размерности. Поэтому, например, позитивная оценка «4» по 4-балльной шкале в соответствии с формулой (3) может оказать существенное негативное влияние на конечный результат D .

Устранение указанного замечания возможно, с одной стороны, с помощью уменьшения нелинейности путем снижения формальной точности вычисления коэффициентов желательности, которая повышается при применении метода расстановки приоритетов на каждой итерации. Однако это существеннейшим образом отразится на шкалах достаточно большой размерности.

С другой стороны, следует указать, что при формировании качественных (лингвистических) характеристик баллов (термов, названий) исследуемых шкал нами был использован модификатор «очень». А в соответствии с положениями теории нечетких множеств и ЛП любой терм может действительно быть образован из соседнего атомарного терма с помощью модификатора «очень», чему в теории нечетких множеств соответствуют нечеткие операции [1; 13; 14]:

• -    концентрации

m % ( очень высокий УУД ) = m 2 ( высокий ) ; (11)

• -    растяжения

т % ( очень низкий УУД ) = m T,⁵ ( низкий ) . (12)

Ориентация на формулы (11), (12) является серьезным обоснованием повышения желательности (в количественном «весовом» понимании) и других позитивных оценок шкал, что еще больше приблизит к действительности интегральный показатель академической одаренности (или интеллектуальной). Причем, без ущерба точности вычислений. Изложенное и будет предметом наших дальнейших исследований.

Таким образом, обращаясь к полученным и представленным в данной статье новым научным результатам по интегральной квалиметрии академической и интеллектуальной одаренностей, мы констатируем факт существенного развития методологии системных исследований в дидактике путем адаптации, совершенствования и разработки новых методов получения интегральных оценок уровней учебных достижений, которым и только которым присуще системное свойство эмерджентности и поэтому необходимо обучать педагогов образователь -ных учреждений. Отдельными результатами наших исследований являются следующие.

• 1.    Обоснована применимость мультипликативного подхода, базирующегося на усовер-

• шенствованной желательности шкале Харрингтона, в процессах квалиметрии знаний обучаемых. Интегральная оценка АО или ИО находится путем вычисления среднего геометрического результатов тестирования, либо среднегеометрического показателя коэффициентов желательности оценок.

• 2.    Совершенствование шкалы проведено для широкого спектра качественных шкал, используемых в дидактике, путем применения математического метода расстановки приоритетом для вычисления количественных показателей желательности оценок.

• 3.    Доказана явная нелинейность шкалы и определены диапазоны соответствующей «нормы» количественно-качественного соответствия оценок с помощью номограмм, либо аналитическим путем.

• 4.    Учитывая особенности формирования качественных шкал с помощью специальных модификаторов, определены направления дальнейших исследований по увеличению количественного показателя желательности большего спектра позитивных оценок при заданном уровне их точности.