Решение задачи №26 ЕГЭ по информатике методом динамического программирования

Рассмотрим задачу №26 из демонстрационного варианта ЕГЭ по информатике и ИКТ за 2017 г. [1 с. 36]

Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 20. Если при этом в куче оказалось не более 30 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 17 камней и Паша удвоит количество камней, то игра закончится победой Вали. В начальный момент в куче было S камней, 1 ≤ S ≤ 19.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания.

• 1.    а) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.

• 2.    У кого из игроков есть выигрышная стратегия при S = 9, 8? Опишите соответствующие выигрышные стратегии.

• 3.    У кого из игроков есть выигрышная стратегия при S = 7? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.

б) У кого из игроков есть выигрышная стратегия при S = 18, 17, 16? Опишите выигрышные стратегии для этих случаев.

Вместо рассмотрения частных случаев, сформулируем общие принципы, определяющие выигрышные стратегии игроков. Для каждого количества S камней в куче выясним, кто из игроков – первый либо второй обладает выигрышной стратегией в данном случае.

Первый игрок может победить при заданном значении S, если он может победить за 1 ход или за 1 ход перевести игру к позиции с величиной S1, при которой выигрышной стратегией обладает второй игрок, которым теперь будет он сам. В случае если все возможные ходы приводят к величинам S1, S2, …, в позициях которых побеждает первый игрок, то в текущей позиции выигрышной стратегией обладает второй игрок.

Таким образом, пользуясь известными результатами для S, где обладатель выигрышной стратегии уже определён, можно получить решение сформулированной выше задачи методом динамического программирования [2 с. 392] в виде таблицы (см. таблицу 1).

Таблица 1. Решение задачи методом динамического программирования

Для определения не только игрока, обладающего выигрышной стратегией, и его первого хода, но и максимального количества ходов, реализующих эту стратегию, достаточно воспользоваться простым правилом. При наличии выигрышной стратегии второго игрока, его максимальное количество ходов T(S) при этом равно максимальному количеству ходов первого игрока max (T(S₁), T(S₂), …), в позициях S₁, S₂, …, которые могут быть получены из S за 1 ход. Если же выигрышной стратегией обладает первый игрок, и при этом он не может победить за 1 ход, но может за 1 ход переместиться в позицию S₁, выигрышную для второго игрока, то его максимальное количество ходов будет на единицу больше S₁.

В качестве примера рассмотрим построение дерева всех партий для S=6 на основе таблицы 1, полученной методом динамического программирования (выигрышная стратегия имеется у первого игрока).

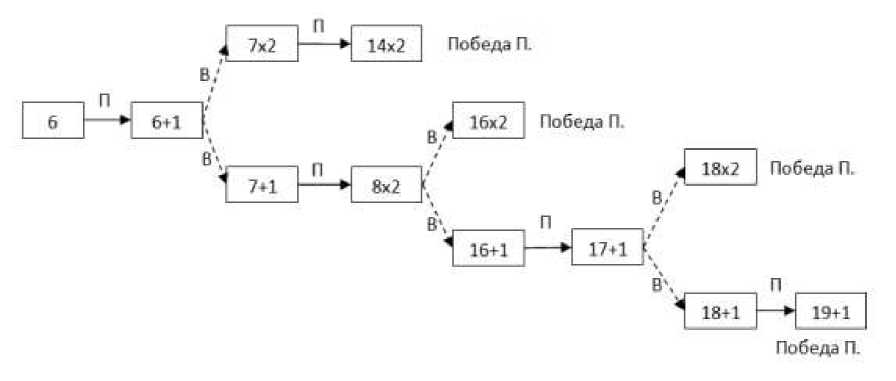
Рис. 1. Построение дерева всех партий для выигрышной стратегии при S=6

Таким образом, образцы авторских решений разработчиков заданий ЕГЭ по информатике и ИКТ ФИПИ [1 с. 38] можно рассматривать как частные случаи предложенного в статье решения.