Резонансы сил и скоростей

Широко известное дифференциальное уравнение d2xdx a      + a    + ax = a, sin го t(1)

2 dt21 dt 0

[1] имеет решение x = x_x + x ₂, где

%! = ae-bt sin(rojt + a)(2)

– собственные затухающие колебания, x2 = A sin(ro t -ф)(3)

- вынужденные колебания, a, a - постоянные интегрирования, b = a1-, ro, = J ro2 - b2

2 a ¹⁰

^ro o =

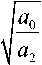
A = I       8°,

(1 -X 2 ) 2 + 4 h ²X ²

(4а)

2 h X ^{tg ф}= 1 —v

! _ ro , _ ba

, X        , h        , 8°        .

ro°        ro°

При подстановках a2 = m , a1 = r, a0 = k, am = F(6)

уравнение (1) превращается в классическое дифференциальное уравнение вынужденных механических колебаний [2–7]:

d2xdx m    + r + kx = F sin rot(7)

dt2

dv или     m— + rv + kJ Vdt = F sinrot.(7а)

При

ro = . (8)

m имеет место резонанс.

Нам известна теоретическая электротехника, объекты и процессы которой математически изоморфны механическим [8–10]; при этом различают два резонанса – резонанс напряжений и резонанс токов.

В 1873 г. Дж. Максвелл ввел первую (из двух) систему электромеханических аналогий, в соответствии с которой напряжение дуально силе, а ток – скорости. В этой связи возникает закономерный вопрос: резонанс применительно к уравнению (7) это резонанс сил или скоростей?

Ответ на этот и связанные с ним вопросы составляет предмет настоящего исследования.

Определение 1. Резонанс сил – это резонанс, возникающий на частоте (8) в механической системе, включающей инертное тело и упругий элемент, при котором развиваемые ими реактивные силы максимальны и противоположны.

Определение 2. Резонанс скоростей – это резонанс, возникающий на частоте (8) в механической системе, включающей инертное тело и упругий элемент, при котором развиваемые ими скорости максимальны и противоположны.

Резонанс сил

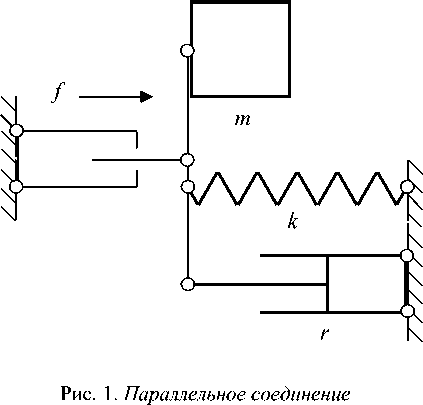
Уравнению (7) соответствует схема параллельного соединения (рис. 1), при котором инертное тело и изменения размеров упругого элемента и демпфера имеют единую скорость, а их реактивные силы складываются. При этом сумма реактивных сил потребителей механической мощности равна силе, развиваемой источником механической мощности, который подобно источнику напряжения в электротехнике можно назвать источником силы.

kF fk =kx =  /=^= ю^( k/ ю- m ю) + r2

гd f-=mw= m ю2 F

=--12 ю^( k /ю-m ю) + r2

81п( ю t - ф ). (9)

81п( ю t -ф ).  (10)

При выполнении условия (8)

f =

kF 81п( ю t - ф )

mkF

=------81п( ю t - ф ) =

r k m mkF

= —----------81п(юt - ф) = ю r kF

=---81п( ю t - ф ) .

ю r

f * =- m

—

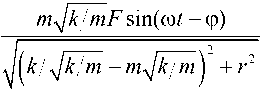
mkF

------81П( ю t - ф ) =

—

r юmmFF . z     ,

—.--- 81п( ю t - ф ) =

Теорема 1 . При выполнении условия (8) в механической системе, состоящей из параллельно соединенных инертного тела, упругого элемента и демпфера, что соответствует уравнению (7), возникает резонанс сил.

Доказательство

В соответствии с (4)–(6)

и

—

ю mF . z, -----81П( ю t - ф ) .

r

Выражения (11) и (13) показывают, что f * равны и противоположны. (9) и (12),

(10) и (14) показывают, что f * и f * максимальны.

Теорема доказана.

A = F k

F

2 \2         22

,  mю I .rm m ю

1--I + 45

k J    4 m2 кk

________________1_____________________

)/ k yj ( к / ю- m ю ) ² + r²

F

ю^( к / ю- m ю ) ² + r²

.

В установившемся режиме x = A 81п(ю t -ф) =

F

=---,                   81п( ю t - ф ) .

юА( к/ ю- m ю ) + r²

Следствие 1.1. В первую (максвелловскую) систему электромеханических аналогий необходимо добавляется следующее дуальноинверсное соответствие – последовательное соединение потребителей электрической мощности при резонансе напряжений дуально параллельному соединению потребителей механической мощности при резонансе сил.

Следствие 1.2. При резонансе сил реактивная сила системы упругий элемент – инертное тело равна нулю, поскольку f k‘ =- f * .

Величину mk по аналогии с электротехникой можно назвать волновым сопротивлением (системы).

Следствие 1.3. Если 4mk > r, то реак- тивные силы, развиваемые инертным телом и упругим элементом, превышают приложен- тельного соединения в соответствии с (2) определяются выражением f = ae-bt sin(м11 + a) = ную силу.

Пример 1. F = 100 Н, м = 2 рад/с, m = 10 кг, к = 40 кг - с^-2, r = 5 кг - с^-1.

Найти f _k ^* и f _m ^* .

k

= ae ^{2 r} sin

k k² _ ----t + a .

m  4 r

В соответствии с (12) и (14)

fk =

40 - 100

2 - 5

sin( м t - ф ) = 400sin( м t - ф ) (Н),

Вынужденные колебания силы на штоке источника скорости для последовательного соединения в соответствии с (3) определяются выражениями

2 - 10 - 100 .          ,

fm =---Sin(м t -ф) =

A =

= - 400sin( « t - ф ) (Н).

Реактивные силы, развиваемые инерт-

7 (1 -X ² ) ² + 4 h ²X ²

V м m

ным телом и упругим элементом, превышают приложенную силу.

Последовательное соединение

m ² k ² m m

1 -м2— + 4—- — м2 — k J     4 r2 k k

V м m

Инертное тело, упругий элемент и демпфер можно соединять не только параллельно, но и последовательно (рис. 2).

I 1 м 1 мm. I---I

\^м m k J

+      2 h X   _ tgф = 7-7-2 = 2

1 - X

k м m

,

+ —

r

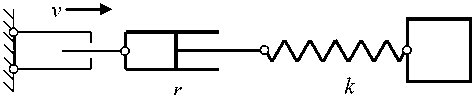
m

Рис. 2. Последовательное соединение

2 r k 1 -м 2 m/k

м m

r м m (1/ м m -м/ k ) f ₂ = A sin( м t - ф ) =

V sin м t - arctg

r (1/ м m - м/ k )

.

r ²

При последовательном соединении к элементам системы приложена единая сила, а скорости инертного тела и изменения размеров упругого элемента и демпфера складываются. При этом сумма скоростей потребителей механической мощности равна скорости, развиваемой источником механической мощности, который подобно источнику тока в электротехни- ке можно назвать источником скорости.

Скорости компонентов системы равны vm = “Jfdt mJ

1dx 1df vk = — k— = ——, vr k dt k dt v = -V cos м t.

f

^, r

v m + v k + vr = v ,

1 df    f    1

---+ — +— fdt = -V cos м t k dt  r  m или

Резонанс скоростей

Справедлива

Теорема 2. При выполнении условия (8) в механической системе, состоящей из после- довательно соединенных инертного тела, упругого элемента и демпфера, что соответствует уравнению (15), возникает резонанс скоростей.

Доказательство

В установившемся режиме

V f =  .                       sin(мt - ф) .

4 [1(м m) - м/ k ]2 +1/ r2

vm = fdt = m

1        V cos( м t - ф )

м m 7 [км m) -м/ k ]2+vr2 ’

v _k

1 df м      V cos( м t -ф )

--=-- 1                            . (17)

^{k dt k} 7[ 1 ( м m ) - м/ k ] 2 +1/ r²

При выполнении условия (8)

1             V cos( ro t — ф )

mm^m izi m j k ju mm mm/ )

—

Vr

J= cos( ro t — ф ) = mk

—

cos( ro t — ф ) =

Vr

--cos( и t — ф ) . го m

km v k = k

V cos( ro t — ф )

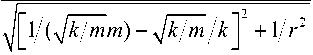
Vr

-j= cos( ro t — ф ) = mk

и Vr cos( ro t — ф ) и Vr ,      .

--- ^v   ^ = — cos( o t — Ф ).  (21) k m mk     k

Выражения (18) и (20) показывают, что v k И v _m равны и противоположны. (16) и (19), (17) и (21) показывают, что v k и vm максимальны. Теорема доказана.

Следствие 2.1. В первую (максвелловскую) систему электромеханических аналогий необходимо добавляется следующее дуальноинверсное соответствие - параллельное соединение потребителей электрической мощности при резонансе токов дуально последовательному соединению потребителей механической мощности при резонансе скоростей.

Следствие 2.2. При резонансе скоростей точка приложения силы к системе упругий элемент-инертное тело неподвижна, поскольку vk =— vm .

Следствие 2.3. Если Vmk < r , то ско- рости, развиваемые инертным телом и упругим элементом, превышают скорость штока источника воздействия.

Пример 2. V = 10 м-с-1,  r = 80 кг-с-1, остальные данные из примера 1. Найти vk и * V m.

В соответствии с (19) и (21)

10 - 80 2 - 10

vm

cos( и t — ф ) = = — 40 cos( ro t — ф ) (м - с '¹ ) ,

*

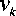
2 - 10 - 80

cos( и t — ф ) =

= 40 cos( и t — ф ) (м - с ^-1 ).

Скорости, развиваемые инертным телом и упругим элементом, превышают скорость штока источника воздействия.

Артефакты

Существуют устройства в удовлетворительном приближении способные выполнять функции источников силы и источников скорости. Источником гармонической скорости может выступать привод с кривошипнокулисным механизмом и маховиком с большим моментом инерции. Источником гармонической силы может выступать шток пневмоцилиндра, полость которого сообщается с полостью другого пневмоцилиндра с диаметром неизмеримо выше, чем у первого, а поршень совершает гармонические колебания.

В работе [11] описана механическая система из двух инертных тел и двух упругих элементов, для которой обнаружено " удивительное явление ": точка приложения гармонической силы остается неподвижной. Это явление, казалось бы, очевидным образом названо антирезонансом. Степень неудачности этого термина можно оценить, применив его к резонансу токов в электротехнике.

В действительности упомянутая система представляет собой суперпозицию " элементарных " систем, рассмотренных выше. По этой причине процессы, происходящие в ней, являются суперпозицией соответствующих процессов, одним из которых и был резонанс скоростей, ошибочно принятый за " антирезонанс " . При этом неподвижность точки приложения гармонической силы ( " удивительное явление " ) соответствует следствию 2.2.

Заключение

Таким образом, можно сделать вывод, что описываемый в курсах теоретической механики механический резонанс является резонансом сил. Ему соответствует параллельное соединение инертного тела, упругого элемента и демпфера. При последовательном соединении этих элементов возникает резонанс скоростей.