"Сквозные " задачи как средство совершенствования математической подготовки бакалавров -экономистов

Постоянно обновляющийся поток информации, а также развитие экономических процессов в современном обществе определяют появление все более высоких требований к выпускникам экономических вузов. Система подготовки компетентных в области экономики специалистов, соответствующих современному уровню, опирается на глубокие знания как экономических, так и математических дисциплин. Вполне очевиден тот факт, что конкурентоспособность специалиста на рынке труда во многом зависит от его умения точно (грамотно, профессионально) моделировать экономические процессы, описывая их математическим языком, поэтому для преподавателей математики в экономических вузах задача повышения математической подготовки стояла и стоит на первом месте.

Не вызывает сомнений, что вооружение студентов-бакалавров экономического направления глубокими теоретическими знаниями по математике не может быть в полной мере выполнено без приобщения их к решению прикладных задач. В связи с этим мы поставили задачу создания методической модели обучения дисциплинам математического цикла в экономическом вузе на основе «сквозных» задач прикладного характера. Для этого

были определены цели, содержание и методы обучения математике в экономическом вузе на основе использования «сквозных» задач в соответствии с определенной направленностью.

Цели методической модели обучения включают:

– обогащение системы взглядов на значимость математики и ее интегральной роли в экономических дисциплинах на основе «сквозных» задач прикладного характера;

– формирование представлений о применении теоретических знаний математики в области экономики;

– овладение умением на основе типовых методик выстраивать математическую модель экономических процессов с дальнейшим ее решением и обоснованием полученных результатов;

– обеспечение достаточной математической подготовки студентов для изучения ими экономических дисциплин и дальнейшего самообразования.

Реализация поставленных целей потребовала создание такого процесса обучения дисциплинам математического цикла в экономическом вузе, важным компонентом которого является содержание, выступающее основой для формирования «сквозных» задач прикладного характера.

Отметим, что в настоящее время основополагающими требованиями к результатам освоения основных образовательных программ бакалавриата являются профессиональные компетенции. В рамках изучения дисциплин математического цикла объективными факторами, способствующими формированию профессиональных компетенций, можно назвать следующие:

– ранняя профессиональная направленность содержания;

– преемственность и «сквозной» характер составления заданий для всех видов учебной работы, учитывающий межпредметные связи;

– компетентностный подход к обучению студентов.

Таким образом, студентов уже на первых курсах необходимо обучать решению задач, в фабулах которых закладываются определенные ситуации, связанные с профилем данной специальности. При этом мы предлагаем использовать в практических занятиях «сквозные» задачи, предполагающие рассмотрение их в течение всего процесса изучения дисциплин математического цикла, точнее, переходящих из одной дисциплины в другую.Тем самым, на наш взгляд, будет осуществляться внутренняя мотивация студентов к обучению, что естественным образом способствует формированию профессиональных компетенций в соответствии с профильной направленностью и, как следствие, повышению качества их знаний и умений.

Остановимся на понятии и структуре математической задачи, в которую, как правило, входят следующие основные компоненты:

• –    условие задачи – данные элементы, свойства и связи между ними;

• –    базис решения задачи – множество факторов, определяющих ее решение (теоретическая или практическая основа этого решения);

• –    решение задачи – способ перехода от условия к результату;

• –    цель задачи – результат решения (неизвестные элементы, свойства и связи между ними).

При этом, если в задаче все основные компоненты представляют собой математические объекты, то она считается чисто математической, а если же математическими являются только внутренние компоненты, т.е. базис решения и само решение, то ее относят к прикладным. Так, И.М. Шапиро выделяет по содержанию задачу прикладного характера, фабула которой раскрывает «приложения математики в смежных учебных дисциплинах, знакомит с ее использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций» [4, с. 5].

Еще раз отметим, что в процессе обучения математике задачам с практическим содержанием отводится особая роль. Во-первых, при анализе и разрешении рассматриваемой прикладной проблемы, заложенной в условии задачи, студенты должны самостоятельно найти пути, позволяющие воспользоваться определенными математическими знаниями, а это естественным образом мотивирует их к более тщательному изучению теоретического материала. Во-вторых, в процессе решения данных задач вырабатываются умения анализировать, сравнивать, синтезировать, абстрагировать, аргументировать, а значит, развиваются логическое, творческое мышление, па- мять, восприятие и многие другие познавательные процессы личности. В-третьих, содержание практических задач раскрывает значение математики в общечеловеческой культуре, достижениях научно-технического прогресса. При этом, приобретая опыт использования различных подходов к решению таких задач, студенты приобщаются к решению актуальных проблем, поставленных реальной действительностью. Тем самым расширяются возможности ориентировать образовательный процесс и на развитие у студентов профессиональных компетенций, позволяющих разрешать проблемы и задачи, возникающие в профессиональной деятельности. Данное основание вкупе с поставленными целями явилось системообразующим при подборе «сквозных» задач для дисциплин математического цикла в экономическом вузе. Отбор содержания таких задач строился на принципах связующей, практико-востребованной, индивидуально-ориентированной, информационно-технологической направленностей. В качестве примера опишем систему заданий, основанных на модели финансовых вычислений, и место их использования в учебном процессе для бакалавров направления «Экономика» профильной подготовки «Финансы и кредит». По данному направлению предусмотрено изучение следующих математических дисциплин [2]: «Математический анализ»; «Линейная алгебра»; «Теория вероятностей и математическая статистика», «Теория игр».

Для дисциплины «Математический анализ»

Задача №1 (тема «Основные характеристики функций»). Вкладчик открывает счет на сумму P с фиксированной процентной ставкой i годовых, начисление которых происходит в конце года, причем а) годовой процентный платеж в каждом расчетном периоде добавляется к наращенной сумме предыдущего периода, а начисление процентов в последующем периоде производится уже на эту наращенную величину; б) начисление процентов осуществляется на постоянную величину, а именно на сумму вклада Р . Составить зависимость наращенной суммы от времени для двух случаев, построить графики полученных зависимостей (функций) наращенной суммы S за период n , выполнить анализ.

Задача №2 (тема «Второй замечательный предел»). Если в задаче 1 (при условии а) проценты начислять не раз в год, a m раз в году, то зависимость наращенной суммы от времени примет следующий вид:

mn

S = P I 1 + j I . к m )

Найти множитель наращения, если начисление процентов будет происходить непрерывно.

Для дисциплины «Линейная алгебра»

Задача №3 (тема «Решение систем линейных алгебраических уравнений»). Если в задаче 1 (при условии б) вкладчик предполагает открыть два вклада, первый вклад на сумму 50 000 руб. под 8% годовых, второй вклад на сумму 100 000 руб. под 5% годовых. Методом матричного исчисления определить, через какое время на его счетах будут равные суммы наращения.

Задача №4 (тема «Матрица. Действия над матрицами»). Подрядчик-строитель заключил договор на возведение через три года следующих строений: 3 жилых дома, 5 детских садов и 9 домов отдыха. Материалами для строительства являются сталь, лес, стекло и краска. Количество сырья, а также рабочей силы на каждый вид строения выражено в нескольких условных единицах и дается следующей матрицей: единица стали стоит 12 у.е., единица леса – 7 у.е., единица стекла – 5 у.е., единица краски – 4 у.е., единица рабочей силы – 10 у.е. В настоящий момент у подрядчика имеются денежные средства в размере а) 6000 у.е.; б) 3000 у.е.

		Сталь	Лес	Стекло	Краска	Рабочая сила
Жилой дом		10	17	8	5	11
Детский сад	А=	7	12	4	3	8
Дом отдыха		5	15	10	4	9

Выяснить, достаточно ли у подрядчика денежных средств для осуществления данного вида работ, если нет, то под какую процентную ставку годовых ему нужно открыть счет, чтобы к началу строительства иметь нужные средства. Расчеты проводить согласно условиям банка из задачи 1 по двум вариантам начисления. Непосредственные вычисления проверить в MS Excel.

Для дисциплины «Теория вероятностей и математическая статистика»

Задача №5 (тема «Числовые характеристики дискретных случайных величин»). Банк выдал k разным заемщикам кредиты на один год в размере Р рублей. В договоре банк начисляет проценты согласно условию а) задачи 1. Найти среднюю прибыль банка, наименьшее целое число, которым должна выражаться процентная ставка, если вероятность невозврата заемщиком кредита равна р, оценить риск банка.

Задача №6 (тема «Непрерывные случайные величины. Плотность распределения и ее свойства»). Предположим, что вкладчик срочного годового вклада может в любой момент востребовать свой вклад. При этом банк выплачивает за действительное время вклада проценты из расчета 4% годовых вместо 9% по срочному вкладу. Каков в среднем потерянный процент вкладчика? Условия банка из задачи 1.

Для дисциплины «Теория игр»

Задача №7 (тема «Игра с "природой"»). Инвестор, вкладывающий деньги в банк, рассматривает несколько возможных решений i = 1, 2,. k , m . Ситуация неопределенна, но известно, что присутствует наличие следующих вариантов: j = 1, 2, ., n. Если инвестор примет i-решение при условии j-ситуации, то он получает доход a

i j ^.

ных решений: А =

( aj ) .

Дана матрица возмож-

' 5 3 10 5 ^

2 2 4 12

8 3 6 ¹⁰ к 1 9 2 7 |

Дать рекомендации инвестору по принятию наилучшего решения и оценить риск операции.

Задача №8 (тема «Принятие решений в условиях риска»). Фирма планирует открыть новое предприятие. На данный момент имеется возможность построить как крупное предприятие, так и небольшое, которое через три года можно расширить при условии высокого спроса на выпускаемую им продукцию. Рассматривается задача принятия решений на пятилетний срок. Эксперты фирмы установили, что на протяжении определенного периода времени вероятность высокого спроса на изготавливаемую продукцию равна 0,75. Стоимость крупного предприятия на данный момент равна 50 млн руб., а небольшого – 10 млн руб. Расширение последнего через три года обойдется фирме в 42 млн руб. Прибыль, получаемая от функционирования производственных мощностей на протяжении 5 лет, приведена в следующей таблице.

Альтернатива	Ожидаемый доход за год,тыс. руб.
	высокий спрос	низкий спрос
Крупное предприятие	9000	2000
Небольшое предприятие	2500	1000
Расширение небольшого предприятия через три года	7000	1500

• а)    построить соответствующее дерево решений, принимая во внимание то, что через три года фирма может как расширить небольшое предприятие, так и не расширять его;

• б)    определить стратегию фирмы на планируемые пять лет (для простоты исключить возможность инфляции);

• в)    решить варианты а и б , предположив, что ежегодная процентная ставка 10% начисления согласно задаче 1 (условие а ).

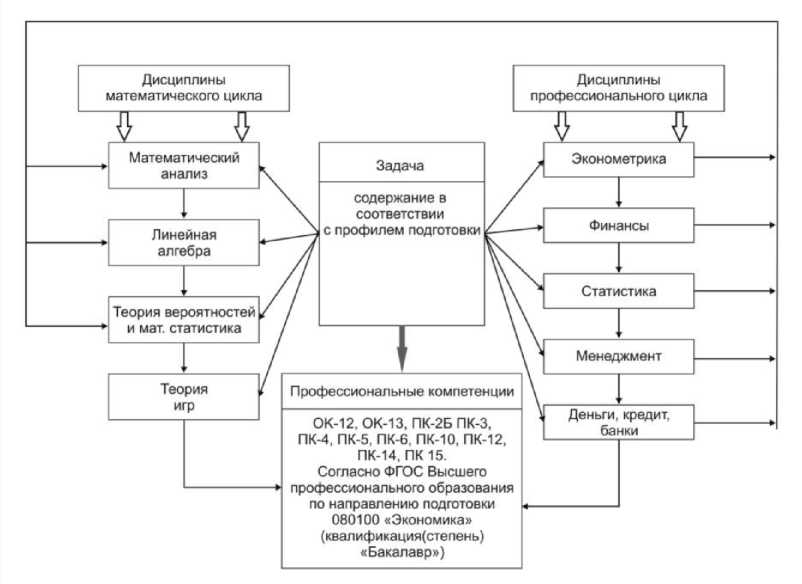
Как видно из содержания задач, все они строятся на основе условия первой задачи, но по мере продвижения по дисциплинам математического цикла их фабулы интерпретируются в соответствии с изучаемым тео- ретическим материалом. В результате осуществляется интеграция дисциплин математического и профессионального циклов и формируются профессиональные компетенции в соответствии с профилем подготовки бакалавров. В целом же созданная интеграционная модель «сквозных» задач в рамках дисциплин математического цикла в условиях обучения бакалавров-экономистов представлена на рисунке.

Таким образом, включение системы «сквозных» задач в процесс изучения дисциплин математического цикла, на наш взгляд, будет способствовать формированию профессиональных компетенций, повышению качества знаний студентов, а также содействовать созданию у будущих специалистов убежденности в полезности и необходимости математических знаний в их профессиональной деятельности. Отметим, что предлагаемая методика «сквозных» задач апробируется в Краснодарском филиале Российского государственного торговоэкономического университета на кафедре математики и прикладной информатики.

Интеграционная модель «сквозных» задач в рамках дисциплин математического цикла