Специальная математическая подготовка в технологическом университете

Реформирование высшего образования в России предусматривает многоуровневый характер процесса обучения. В условиях федерального образовательного эксперимента в плане подготовки высококвалифицированных специалистов, отвечающих современным требованиям, одной из центральных проблем является реализация идеи непрерывного образования.

Математическая подготовка инженеров и магистров является основой их профессиональной подготовки. Недостатки в системе непрерывной математической подготовки на старших курсах создали предпосылки к разработке дидактической модели математической подготовки инженеров и магистров на старших курсах в технологическом университете при многоуровневом образовании, которую будем называть специальной математической подготовкой.

Введение многоуровневого университетского образования в соответствии с Болонским процессом предполагает изменение содержания, форм и методов обучения, в частности, изменение содержания, форм и методов математической подготовки.

Математическое образование в технологическом университете на 1-2 курсах является фундаментом полного высшего образования инженера и магистра. Профессиональная компетентность выпускника технологического университета во многом зависит от фундаментального математического образования, которое ориентировано на широкие направления естественнонаучного и технического знания, охватывающие значительную совокупность близких специализированных областей, на достижение глубинных, межпредметных связей.

Математическая составляющая профессиональной компетентности предполагает формирование профессионально-прикладной     математической компетентности на 1-2 курсах; закрепление ее в общепрофессиональных дисциплинах (3-4 курсы); дополнительное овладение прикладными математическими методами в процессе специальной математической подготовки на уровне, достаточном для применения этих методов при решении профессиональных задач и для дальнейшего саморазвития специалиста.

Различия в математической составляющей профессиональной компетентности инженеров и магистров связаны со следующими моментами: инженеры должны достичь уровня практической ориентации в использовании математических методов, а магистрам необходим уровень исследовательской ориентации, т.е. выбор и использование математических методов в проблемных ситуациях.

Нами разработана и обоснована дидактическая модель специальной математической подготовки при многоуровневом обучении в технологическом университете. Специальная математическая подготовка выполняет профессиональную (основы моделирования специальных математических знаний) и развивающую (развитие готовности к самообразовательной деятельности) функции, что требует личностно-деятельностного, компетентностного и интегративного подходов к формированию информационного и процессуального блоков. Личностнодеятельностный подход организует активную познавательную деятельность в процессе специальной математической подготовки с переходом к самообразованию. Интегративный подход позволяет представить в виде целостной системы прикладные математические методы и их применение в специальных дисциплинах, при решении профессиональных задач. Компетентностный подход необходим для формирования математической составляющей профессиональной компетентности, как способности инженера и магистра применять прикладные математические методы к решению профессиональных задач. Основными принципами проектирования специальной математической подготовки на старших курсах, отражающими закономерности развития содержания профессионального образования, интеграции математики и различных предметных областей знаний, являются принципы индивидуализации, оптимального сочетания фундаментальности и профессиональной направленности, самостоятельности познания. Организация процесса обучения с учетом индивидуальных и профессиональных различий необходима для профессионального становления специалиста. Индивидуализация реализует личностно-деятельностный подход и позволяет в процессе специальной математической подготовки учесть интересы каждой специальности и каждого будущего специалиста. Принцип индивидуализации реализуется посредством обеспечения студентов возможностью проведения консультаций с преподавателями, возможностями постоянной самопроверки в образовательном процессе, с помощью использования информационных технологий, выполнения докладов, рефератов, курсовых работ. Самостоятельность познания выражается в самостоятельном приобретении знаний в области прикладных математических методов, необходимых для теоретической и практической подготовки инженера и магистра. Принцип самостоятельности познания связан как с личностно-деятельностным, так и с компетентностным подходом. Принцип оптимального сочетания фундаментальности и профессиональной направленности способствует формированию математической составляющей профессиональной компетентности через межпредметные связи, интегрированные курсы, использование прикладных математических методов к решению прикладных задач.

На основе анализа Государственных образовательных стандартов, действующих в технологическом университете, учебных планов, потребностей специальных дисциплин и анализа профессиональной деятельности инженеров и магистров разработано содержание специальной математической подготовки (рис.1).

Содержание специальной математической подготовки на старших курсах технологического университета включает в себя дисциплины:

• •    Специальные главы математики;

• •    Дополнительные главы математики.

Содержание математической подготовки

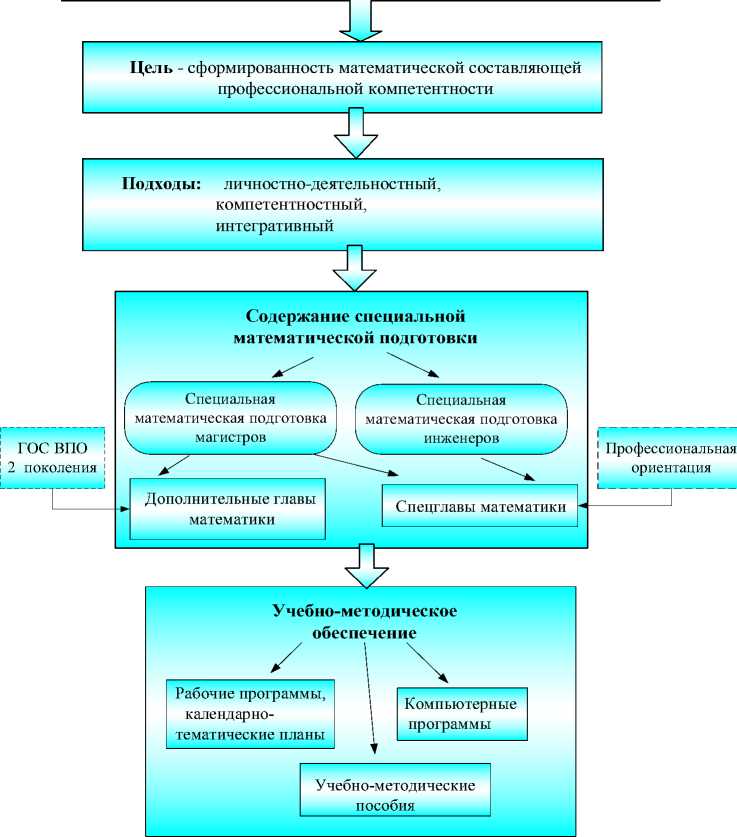
Рис. 1. Модель проектирования содержания специальной математической подготовки

Дисциплина «Специальные главы математики» продолжает математическую подготовку студентов на 3, 4 или 5 курсах. Дисциплину «Дополнительные главы математики» изучают магистры направления 240100 – «Химическая технология и биотехнология». Состав и содержание специальных дисциплин определяется требованиями специализации студента, поэтому специальная математическая подготовка должна регулироваться принципом оптимального сочетания фундаментальности и профессиональной направленности. При разработке содержания специальной математической подготовки на старших курсах технологического университета важнейшей является задача наиболее рациональной компоновки фундаментальных и профессионально значимых разделов высшей математики, в которой бы учитывались иерархические особенности и внутренние логические связи, учет уже имеющихся математических знаний, полученных во время изучения курса высшей математики на 1-2 курсах, взаимосвязь с курсами общетехнических и специальных дисциплин и потребностями дипломной (у специалистов) или магистерской работ. Четкое определение инвариантной и вариативной составляющих, а также распределение времени на их изучение легли в основу формирования содержания учебной программы курса специальной математической подготовки для рассматриваемых специальностей. Как показала практика, на старших курсах технологического университета желательно ввести такие специальные курсы для всех специальностей.

С точки зрения инвариантной и вариативной составляющих в курсах «Специальные главы математики» и «Дополнительные главы математики» выделены:

• 1.    Общие разделы, предназначенные для всех технических специальностей – инвариантная составляющая.

• 2.    Специальные разделы, содержащие прикладные математические знания, рассматривающие конкретные прикладные задачи и обеспечивающие межпредметные связи, – вариативная составляющая.

Анализ учебных планов подготовки магистров направления 240100, учет профессиональной составляющей математической подготовки каждой из специальностей, опрос преподавателей, проводящих специальную подготовку магистров, а также использование математических понятий и методов в магистерских диссертациях позволили выделить разделы математики, необходимые для изучения.

Проектирование процессуального блока реализует дидактический процесс на основе принципов: индивидуализации, оптимального сочетания фундаментальности и профессиональной направленности, самостоятельности познания, применением интегративных форм аудиторных занятий и разработанных дидактических материалов. Входной контроль характеризует уровень сохранения знаний по математике, т.е. опосредованно и уровень использования математических методов в циклах общепрофессиональных и специальных дисциплин, курсовых работах. Используются интегративные формы лекций с привлечением для иллюстрации профессиональных задач. Самостоятельная работа включает в себя подготовку и выполнение студентами рефератов, докладов. Проверка остаточных знаний, текущий и окончательный контроль осуществляются с рейтинговой оценкой.

Технологическая схема дидактического процесса представлена на рис.2.

Экспериментально проверена эффективность специальной математической подготовки на старших курсах при многоуровневом обучении в технологическом университете в процессе обучения студентов старших курсов дисциплинам «Дополнительные главы математики», которую изучают магистры направления 240100 – «Химическая технология и биотехнология» и «Специальные главы математики», преподаваемой студентам четвертого курса специальности 170600 «Машины и аппараты пищевых производств».

В экспериментальных группах инженеров и магистров обучение проводилось по измененным учебным программам специальной математической подготовки. Была введена рейтинговая система оценки знаний студентов, систематически отслеживался процесс обучения с выявлением недостаточно изученных вопросов программы и своевременным внесением изменений в учебный процесс. Для каждой группы с целью педагогического мониторинга строились диагностические карты. В качестве самостоятельной работы студентам были предложены темы докладов и рефератов. Также студентам предлагалось самостоятельное определение темы реферата или доклада, исходя из использования математических методов в дипломной (магистерской) работе или в изучаемых ими специальных дисциплинах.

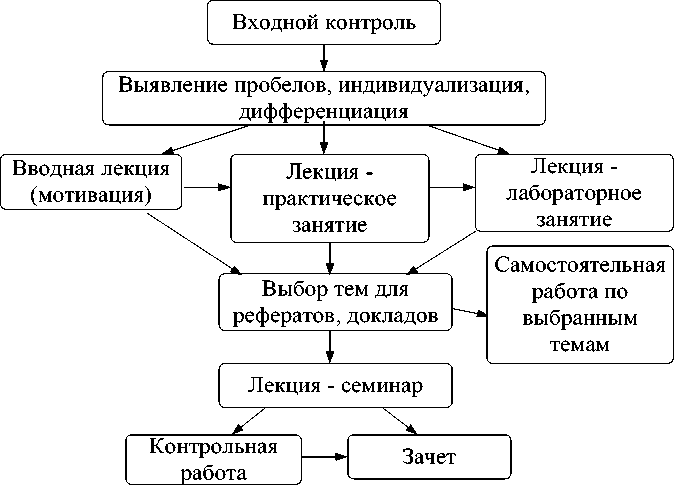
Рис.2. Технологическая схема дидактического процесса специальной математической подготовки

Качество усвоения знаний диагностировалось посредством рейтинговой системы оценки знаний студентов и индивидуальным коэффициентом усвоения математических методов в аспекте сформированности математической составляющей профессиональной компетентности ^kст . . По итогам рейтинговой системы оценки знаний нами были рассчитаны индивидуальные коэффициенты сформированности математической составляющей. В результате 0,7 <  к <  1 имеют 67% студентов-инженеров и 100% студентов-магистров, что свидетельствует об эффективности реализации дидактического процесса специальной математической подготовки.