Тамақ өндірісіндегі кептіру кинетикасын математикалық модельдеу

ҒТАХР 65.01.77                                     

Кіріспе

Тамақ өнімдерін кептіру процестері – тамақ технологиясының ең маңызды бағыт-тарының бірі, өйткені олар өнімнің сақтау мерзімін ұзартып, физика-химиялық қасиеттерін тұрақтандыруға мүмкіндік береді. Соңғы жылдары бұл процестердің күрделенуі мен энергия тиімділігі мәселесі өзекті болып отыр. Осыған байланысты кептіру кинетикасын дәл сипаттайтын математикалық модельдер құру қажеттілігі туындады.

Зерттеу тақырыбының өзектілігі – кептіру кезінде жүретін жылу және масса алмасу құбылыстарын теориялық негізде сипаттай отырып, өндірістік процестердің тиімділігін арттыру. Бұған дейінгі зерттеулер (Лыков, Бухмиров, Khan және Akter еңбектері) негізінен физикалық модельдерге сүйенген, алайда процестің көппараметрлі табиғатын толық қамти алмайды.

Зерттеу объектісі – тамақ өнімдерін кептіру процесіндегі жылу және массаалмасу.

Зерттеу пәні – кептіру кинетикасын сипаттайтын математикалық модель.

Мақсаты – кептіру процесінің темпера-туралық және ылғалдық өрістерін сипаттайтын теңдеулер жүйесін құрастыру және оның тиімді режимдерін анықтау.

Әдістер: дифференциалдық теңдеулер жүйесін сандық әдіспен шешу, эксперименттік салыстыру, жылу және массаалмасу заңдарын қолдану.

Гипотеза – кептіру процесінің кинетикасын математикалық түрде сипаттау арқылы өнім сапасын сақтап, энергия шығынын азайтуға болады.

Заттардың бiр фазадан екiншiсiне ауысуының негiзгi заңдылықтарын массаны тасымалдау теориясы айқындайды, соған сәйкес масса беру жылдамдығы қозғаушы күшке пропорционалды болады. Оның шамасы фазалы^ тепе-тецдзк зацдары негЫнде анықталады. Массаның тасымалдануының қозғаушы күштерін концентрациялар, температуралар мен қысымдардың айырмашылықтары арқылы есептейді. Бір фазаның шегіне диффузиялық ағынға перпендикулярлы F беті арқылы фазалардың бөліну шекарасына келетін заттың мөлшері Фик зацымен аныкталады [1]:

М = —DFAct.

мандат D - пропорционалдык (диффузия) коэффициент); А с - концентрация айырмасы (козFаушы кYш); т - копиру уакыты.

Фазалар бөлімінің шекарасына (немесе шекарасынан) зат мөлшерінің жиынтық көшуі массалык берудш, тецестiрiлуiмен айкындалады:

М = pF(cT - cb)t, мандат в - пропорционалдык (массалык кайтарым) коэффициент): сг, св - фазалардыц бөліну шекарасында және ағынның ішінде (ядросында) шоFырлану.

Массаберу коэффициенті диффузин коэффициентінен өзгеше кинетикалық сипаттама болып табылады жэне диффузия коэффициенте (физикалык константа), v ағынының жылдамдығына, ρ тығыздығына және р заттыц туткырлытына, 1 1 белшектершш, геометриялык елшемдерше, 1 2 аппараттарына және т.б. байланысты болады. Жалпыланған түрде бұл тәуелділік [2] функциясымен усынылуы мYмкiн:

Р = F(D,v,p,n,l i ,l₂ .„)

немесе критерналды формада:

Nu_d = A Re ^m Рг ^

мундаты Nud = в ID. Pr o = v /D - Нуссельт пен Прандльдш, диффузионды сандары; Re-Рейнольдс саны; l -аныктаушы геометриялык елшем; v - кинематикалык туткырлык коэффициент).

Келтірілген арақатынастар жылу және масса беру процестерінің аналогтары туралы куәландырады, бұл математикалық үлгілерді

құрастыру әдістерін қорытындылауға мүмкіндік бередк

Масса алмасу процестерінің жұмысын талдау үшін кинетикалық заңдылықтар өте маңызды болып табылады, олар массаалмасу процесінің әрбір түрі үшін өзіндік ерекше нысанFа ие.

Зерттеу материалдары мен әдістері.

Массаалмасу процестері қоспадан қандай да бір компонентті (затты) бөлуге немесе ажыратуға (тазартуға) арналғандықтан, бұл процестердің негізгі технологиялық міндетін қажетті тазалық дәрежесіндегі (96% спирт, 8% ашытқы ылғалдылығы және т.б.) белгілі бір заттың берілген мөлшерін алу ретінде тұжырымдауға болады. Кейбір жағдайларда (мысалы, тазарту кезінде) міндет басқаша тұжырымдалуы мүмкін: мысалы, негізгі өнімде зиянды компоненттш, болуы.

Негізгі технологиялық міндетке қол жеткізілген жағдайда массаалмасу процесінің сапасы жылу, су, электр энергиясының, күрделі, пайдалану және т.б. шығындарымен бағаланады. Жалпы бағалау туралы қосымша дайын өнім бірлігін өндіруге жұмсалынғанн шығындар болып табылады. Осы негiзде жаппай алмасу процестерiн жетiлдiрудiң жалпы мақсаттарын да тұжырымдауға болады: бөлу тазалығының дәрежесiн арттыру және өнiм бiрлiгiне қатысты меншiктi шығындарды төмендету. Бұл мақсаттарға қолданыстағы аппаратураны жетілдіру және жаңа аппаратураны әзірлеу, оңтайлы режимдерді таңдау, аппараттар жұмысының тұрақтылығы мен сенімділігін арттыру, басқару процестерін автоматтандыру және т.б. жөніндегі көптеген жеке міндеттерді шешу аркылы кол жетктзкту) мYмкiн.

Мұндай жеке мәселелерді көптеген жағдайларда математикалық модельдер арқылы шешуге болады [3,4]. Барлық жаппай алмасу процестерінің ішінен тамақ кәсіпорындарында таралғандардың бірі, ол кептіру процесі болып табылады. Мұнда математикалық модельдеу әдістерімен масса алмасуды жетілдірудің кейбір мшдеттерш шешуд), сондай-ак суйык жэне газ фазаларының масса алмасуының ерекшелігіне байланысты айдау процесін модельдеу ерекшелжтерш карастырамыз.

Нәтижелер және оларды талқылау

Кепыру кинетикасыныц математи-калык модельдер)

Кепыру - ол типык масса алмасу процей болып табылады, мұнда ылғал кептірілетін материалдан кептіру агентіне ауысады. Түрлі тамақ өнімдерін, жартылай фабрикаттарды және шикізатты (дән, уыт, барду, азықтық және тағамдық ашытқылар, крахмал және т.б.) Kenmipegi. Кейбiр тамац eHgipicmepiHge Kenmipy -негізгі технологиялық процесс (кептірілген нан, құрғақ сүт, жұмыртқа ұнтағы, құрғақ жемістер мен көкөністер өндірісі) болып табылады. Кептіру процесі кептірілетін өнімге жылу әкелумен байланысты, соның арқасында ылғал буланады. Кептіргіш агент ретінде ауа, қыздырылған бу және кептірілетін материалдан

Vo to ^о

буланатын ылғалдылықпен қанықтырылатын оттыц газдары цолданылады.

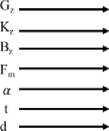
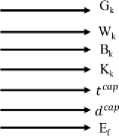
Кептіру процесінің негізгі параметрлері ретінде кептірілетін материал мен кептіру агентшщ сипаттамалары болып табылады (1-сурет): G шығын, материалдың бастапқы ылғалдылығы (немесе ылғалдылығы), оның температурасы, цозFалыс жылдамдыFы v , цабаттыц цалывдьны h .

Сурет 1. Кеппру процесшщ параметрл1к схемасы

Кептіру процесінің негізгі технологиялық мақсаты сапаны сақтай отырып, кептірілетін өнім ылғалдылығының берілген мәнін қамтамасыз ету болып табылады. Процестің сапасы алынған ылғал массасының бірлігіне қатысты меншікті шығындармен бағаланады. Басқарылатын параметрлер мен басқарушылық әсерлерді таңдау зерттеу міндеттерімен айқындалады. Көбінесе басқарылатын параметрлер ылғалдылық пен кептіру шығындарын қабылдайды. Кептірілген материалдың сапасы, әдетте, өнімнің сапасы негізгі шектеуі болып табылады. Кептіру кезінде материалдың сапасы қыздыру температурасы мен экспозициямен анықталатындықтан, бұл параметрлер - нeгiзгi шектеулер. Басцару әсерлерін кептіру агентінің параметрлері: шығын (жылдамдық) және температура, ал кейде кептірілетін материалдың шығыны ретінде цабылдайды.

Кіріс және шығыс параметрлері арасындағы байланыстарды орнату үшін әртүрлі тәсілдер мен әдістер қолданылады. Бұл байланыстар материалдық және энергетикалық теңгерім теңдеулерін, гидромеханика, жылу және масса алмасу заңдарын және т.б. пайдалану негізінде талдамалы түрде белгіленуі мүмкін. Мысалы, кептірілетін материалдың бастапқы және соңғы ылғалдылығының арасында байланыс орнату үшін кептіру кинетикасының теңдеуі, ал кептірілетін агенттің температурасы мен кептірілетін материал арасында тәуелділікті орнату YmiH — жылу алмасу тeцдeyi пайдаланылады. Параметрлердің көп саны арасында байланыс орнататын неғұрлым күрделі модельдер үшін барлық аталған талдамалық және эксперименттік тәуелділіктерді бірлесіп қарау қажет. Параметрлер арасында байланыстар орнатудың эксперименттік әдістері 9pтYpлi жоспарлар - бeлсeндi жэне пассивтi әдістер бойынша физикалық немесе заттай модельдер жасауды талап emeдi.

Кeптipy процесшщ экономикалыц кер-сеткіштері жабдықтың құнын, жұмыстарды орындауға арналған қолданыстағы нормалар мен бағаларды ескере отырып, әртүрлі модельдер негізінде тікелей өлшеу немесе есептеу арқылы алынған техникалық сипаттамалар негізінде eсeптeлyi мумкш.

Кептіру үш кезеңнен тұратындықтан, қыздырудың, кептірудің және кептірілетін материалды салқындатудың математикалық үлгілерін жасау кезінде масса мен энергияны берудің негізгі заңдары қолданылады. Кептіру кезінде негізінен конвективті массаалмасу орын алгандыцтан, гидродинамиканыц нeгiзгi зацды-лыцтарын да ескеру цажет.

Кептірілетін материалды қыздырудың, кептірудің және салқындатудың математикалық үлгілерін жасау кезінде осы заңдылықтарды сипаттайтын теңдеулер әртүрлі нысанда пайдаланылады. Кептіру процесін талдау үшін әдетте ылғалды денелердегі жылу және ылғал

өткізуді сипаттайтын дифференциалды теңдеу-лер жүйесін негізге алады.

^ku^u + k^t + k^P ^l =k₂₁V ² u + k₂₂V ² t + k₂₃V ² P ^k^u + k^t + k^P^

К коэффиценті ылғалды материалдың термодинамикалық және жылуфизикалық қасиеттерімен сипатталады

,               ,                 ,         kp k11   am’k12   amS’k13   „

P o

^{; k} 21

2c

~' ^k 22

= a + -amS; C

k 23 = sr = ^Y S p , k₃ i

^ca m _r ’ ^k 32

^ P

-ca m

^C p

^’ ^k 33

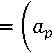
-ca m

^C p

Sp}

Мұнда қосымша мынадай белгілер енгізілген:

^дЬ + ^ + дЬ - Лаплас операторы; ^a = ^/^C p

- температура өткізгіштік коэффициенті; a m -

ылғалдың диффузия коэффициенті; δ - ылғал термодиффузиясының салыстырмалы коэффициенті; δp-термоградиенттік коэффициент; ε - фазалық өзгеру критерийі; r - фазалық айналудың үлестік жылуы; kp - ылғалды сүзгілеу тасымалдау коэффициенті; с - материалдың келтірілген меншікті жылу сыйымдылығы; ср - кеуекті денедегі ылғалды ауа сыйымдылығының коэффициенті; х, у, z - координаттары: ρ0 - ылғалды дененің құрғақ скелетінің тығыздығы.

Бір өлшемді міндеттер үшін жалпы қысым градиенті болмаған кезде теңдеу жүйесі

оңайлатылады

dt     д f - dt\

^Ср 0З-т = Тх^(ХТ х ) ^{+ еГр} 0

ди dt

=  (am у + amS дх m дх    m дх.

ЗиЛ дт ( )}

Мұнда a m , δ, λ, c, ε, r барлық жылу физикалық және термодинамикалық сипатта-малары t температурасы мен ылғал құрамының функциялары болып табылады.

Келтірілген теңдеулер жүйесін шешу үшін температураның және ылғал құрамының дене ішінде уақыттың бастапқы сәтінде таралуын (бастапқы жағдайлар), дененің геометриялық нысанын және қоршаған ортаның дене беті арасындағы өзара әрекеттесу заңын (шектік жағдайлар) білу қажет. Бастапқы және шекара шарттарының жиынтығы ең қарапайым жағдайда шеткі жағдайларды құрайды.

Шекара шарттардың берілу тәсілдері

Шекаралық шарттар төрт тәсілмен берілуі мүмкін. Бірінші түрдің шекаралық шарты дене бетіндегі температураны уақыт бойынша бөлу тапсырмасынан тирады, яFни t n ( т ) = f ( т ) (Дирихле міндеті), екінші түрдегі - дене бетінің әрбір нүктесі үшін жылу ағынының тығыздығын (температурадан туындайтын) уақыт функциясы ретшде q n (т ) = f (т ) (Нейман мшдет1), Yшiншi түрдегі - қоршаған орта температурасының тапсырмасы мен жылу алмасу заңдылығы бойынша:

q_n = a[t_n(r) - t_c(T^], (3)

мұнда t с – қоршаған ортаның темпера-турасы

Төртінші түрдің шекаралық шарты жылу өткізгіштік заңы бойынша дененің қоршаған ортамен жылу алмасуына немесе бетінің температурасы бірдей болған кезде жанасатын қатты денелердің жылу алмасу жағдайына сәйкес келеді (мінсіз жылулық байланыс).

Дене ішіндегі температураны уақыттың бастапқы сәтінде бөлу бастапқы шартпен беріледі t= (x, у, z, 0)= f(x, y, z).

Температураны біркелкі бөлген кезде бастапқы шарт t (x, y, z, 0) =t0 = const.

Шешімнің бірдейлігі туралы теоремаға сәйкес, егер f (x, y, z, τ) функциясы дифференциалды теңдеуді және бастапқы шектік жағдайларды қанағаттандырса, онда ол біртекті болып табылады.

Берілген шеткі жағдайлардың болуы қарапайым жағдайларда жылу өткізгіштіктің тікелей міндеттерінің талдамалық шешімдерін алуға, яғни келесі функцияны табуға мүмкіндік береді.

t п =f(x,y,z,τ).

Жылу алмасудың шекті шарттарына ұқсас массаалмасу кезінде дене бетінің қоршаған ортамен өзара іс-қимылы да төрт тектің шекті шарттарымен сипатталуы мүмкін.

Бірінші түрдің шекаралық жағдайлары дененің үстіңгі бетіндегі диффузиялық масса тасымалы әлеуеті қоршаған ортадағы масса тасымалы әлеуетіне тең болған жағдайға сәйкес келеді; екінші түрдегі - бірінші кезеңде кептіру қарқындылығы тұрақты болғанда, ал екінші кезеңде төмендегенде ылғалды денелерді кептіру кезінде массаалмасу жағдайы. Демек, шекті жағдайларда уақыт функциясы gm = f (τ) ретінде зат массасы ағынының тығыздығы беріледі, ал жеке жағдайда - gm = const.

Үшінші түрдің шекаралық жағдайлары жылу алмасудың шекаралық жағдайларына ұқсас, ал төртінші түрі екі орта арасындағы молекулярлық жылу алмасуды сипаттайды. Жалпы жағдайда шекаралық шарттарды былай жазуға болады:

^-АШ + ^q " (^T) — ^{r (1} — e^nW = °]

* ⁿ                                     > (4)

a ^{m P}°(£)_n + ^{a m P}°⁸(^) + ^q m (^T) = °)

мұндағы q n , q m - беттегі тиісінше жылу мен ылғалдың үлестік ағындары.

τ = 0 кезінде бір өлшемді ағын үшін бастапқы шарттардың түрі мынадай:

m = f (x) және t м = f 1 (x).

Теңдеу жүйесі (1) және шекаралық шарттар ылғалды денелердегі және бинарлық бу-газ ортасындағы (кептіру агенті) сұйықтық-тардағы конвективті диффузия кезіндегі жылу және масса алмасудың математикалық сипаттамасын құрайды. Жылжымалы орта үшін теңдеулерге ортаның қозғалыс жылдамдығын қамтитын мүшені енгізу қажет. Шекаралық жағдайларды жазу нысаны жылу және масса алмасу түріне, ортаның геометриялық нысанына және координаталардың таңдалған жүйесіне байланысты болады.

Материалды қыздырудың, кептірудің және салқындатудың математикалық үлгілерін құру кезінде келтірілген математикалық тәуелділіктер әртүрлі жорамалдарды енгізумен жеңілдетіледі, олар математикалық үлгілердің дәлдігін төмендетеді, бірақ күрделі процестерді шешу үшін салыстырмалы түрде қарапайым және қолжетімді әдістермен және құралдармен ұсынуға мүмкіндік береді.

Мұндай жорамалдар күрделі көп өлшемді денелер мен кеңістіктерді бір өлшемді болуы: кеңістіктер мен күрделі пішінді денелерді қарапайым элементтерге бөлу; температура мен ылғал құрамының өзгеруінің қаралып отырған диапазондарындағы жылу физикалық және термодинамикалық сипаттамалардың өзгермеуі; соңғы нәтижелерге елеусіз әсер ететін мүшелерді теңдеулерден алып тастау және жазба нысанын жеңілдету үшін координаттар жүйесін өзгерту.

Мұндай сипаттамалардың күрделілігіне және жеткіліксіз дәлдігіне, сондай-ақ теңдеу жүйелерін шешу әдісінің болмауына немесе күрделілігіне байланысты кептіру процестерін сипаттаудың неғұрлым қарапайым нысандары жиі пайдаланылады.

Кептіру кинетикасы кептіру қисық сызығының әртүрлі нысандары түрінде ұсынылады. Ең кең таралған нысан А.В. Лыковтың теңдеуі болып табылады:

W =W_p + (W_H- W_p)exp(-KT) (5)

мұндағы W, Wp, Wн. - материалдың ағымдағы, тепе-теңдік және бастапқы ылғалды-лығы; k - ортаның температурасы мен ылғалдылығының функциясы болып табылатын кептіру коэффициенті, k = f (t, φ). Кейбiр жағдайларда жазудың мынадай нысанын ұтымды қолдануға болады:

W=Wp+(Wн-Wp)exp(-а+b/2 τ)τ, мунда а, b - ылFалдын, материалмен байланысын сипаттайтын коэффициенттер. Осы материал Yшiн тепе-тендш ылFалдылыц Wp = f (t, ф) кепт1ру агентінің температурасы мен салыстырмалы ылғалдылығының функциясы болып табылады. Сондықтан, Wy.n = Wh - Wp жэне Wy = W - Wp (қашықтағы ылғал) белгілерін пайдалана отырып, кептіру кинетикасын келесі түрде жазамыз:

W у =W_y .м exp - {k(t,9)(a+b/2 t)t} (6)

Бұл теңдеуде k (t, φ) режимді, ал (a + b/2 τ) - ылгалдын, материалмен байланысын сипат-тайды. Осы сипаттамалардың екеуі де кептіру қисық сызықтарының сипаттамаларын белгілі деп есептей отырып, эксперименттің көмегімен белгшейдь

Дифференциалды формадағы (5) немесе (6) тендеуд! усына отырып жэне АВМ-дагы осы дифференциалды тендеуд! жинактаудын цурыл-ымдық схемасын жасай отырып, кинетиканы зерттеуге арналған модельді алуға болады. Осы салыстырмалы қарапайым міндетті шешу үшін автоматты басқару жүйелерінде арнайы есептеу құрылғысы қолданылады, бұл өнімнің бастапқы ылғалдылығы өзгерген кезде кептіру кинетикасын есептеу міндеттерін бірнеше рет шешуге мYмкiндiк беред1.

Кепт1ру  процесшде  астыктын ылгал- дылыгын аныцтау мш.дет!

(1) тендеулер жYЙесi тYрiндегi ен1м мен кептіру агентінің ылғал құрамы мен температура турынын, математикалыц сипаттамаларына непз-делген модельдер неғұрлым күрделі болып табылады. Осындай математикалық үлгілерді курастырудын мысалы ретшде кептру про-цесінде ылғал құрамы мен температура өрісінің математикалық сипаттамасы бойынша астықтың ылғалдылығын анықтау міндетін қарастырайық. Бұл сипаттама бастапқы шекаралық шарттармен б1рге мынадай турде болады:

бастапқы шарттары

^ + u2^-am (^ + 1 .^) = ⁰

адт      дх       ддг2 г дг J

^ + „3^ + ^^ - tc^—^ + w дт       дх     с^р                     С3 хдт      ‘

и(т, X) = ^3 J* tu(t, x, r) dr

t ⁽т, 0) = f ⁽т) и (0, x, r) = u0 (x, r) t (0,x) = f 2(x)

I

л

Э = 0 (7)

³ дх

шекаралыц шарттары жэне ( т, 0, r) = и⁰ ( т , r)

^д^(т,x,R) дг

( B(t, V cq) ,

--„ _m  ^(uR ^{- U} 0)’ ^U R ^ ^и г ^a m ^(t )                            /q\

_ ^ ^(t , Vc.^q) с            u      _n

(иг U0),UR > Ur am(t)

мундагы du/dr (t, x, R) = 0 - симметрия шарты: R — белшектер радиусы: А, В — эмпирикалыц коэффициенттер; x, r — кепт1ру камерасынын, узындыгы жэне астыц цора-бынын, радиусы бойынша координаттары.

Келтірілген екі теңдеу жүйесі материал мен кептіру агентінің айқаспалы қозғалысы жағдайында астықты тығыз қайнаған қабаттарда кептіру процесін сипаттайды. Егер режим бұзылмаса, яғни кептіру процесі стационарлыц жагдайда етсе жэне du/d т = 0; d t /д т = 0 болса, онда тендеу:

ди _ am(f) fd2u   1 ди\ дх     U3  ддг2   R dr)

дду _ Avc.a ,    — t} — iPBQ^a) , дх    c3p3v3 V c'a              c3v3R

— t)

(ur

—

л

U p )

^^ = (x, 0) = О(симметрии)

бастапкы шарттары:

u (0,r) = u o (r); t (0) = t o (11)

жэне шекаралык шарттары:

ди <х- ^R)={

^— 11^ ^(U R ^—U P ^{) U} R ~^U r — B⁽t,^v c.a ) (u —u_p).U_r > U

um(t)    ^{r      pJ R}

Тецдеу жYЙесiне кешу кезiнде (10-12) кептiрудiц орташа жылдамдыFыныц устщп бетiндегi ылFал курамымен байланысы ескерыген:

R

Au =

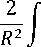
гАидг

2 ди 2 ди ди    ди ди 2В

= R*dr = RdR*dT^{+V 3} dX ^— dX ^— ~R~^{(U R — Up}^

Бұрын жылу тасығыштардың температурасын бөлу міндетін шешу үшін қолданылатын тура

9дiстi пайдалана отырып, жеке туынды теңдеулер жүйесін кәдімгі дифференциалды тецдеулер жYЙесiне келтiремiз, акырFы-айырмашылык аракатынастарды жазамыз:

^ди к _ ^и к+1 ^и к-1 ^{д и} к _ ^и к+1 ^{+ 2и} к + ^и к-1

дЁ        2h     дг ²            R²

мунда k= 1, 2, 3, ...,n - 1; n - r= R-ге катысты тузудiц немiрi; h - кептiру материалыныц радиусы бойынша интервалы.

r = kh екенiн ескере отырып, аламыз:

⁽A^u) k = —^ ^((2к + Х^)и к ^— 4к^и_к + ⁽2к ^{— 1)и}_к -1 )’ соцFы немiрлi k=n тYзуi Yшiн:

2 /ди  ип — ип-1\ + 1 du п  n\дR      п / R  dr’ мунда n- r = R-ге катысты тYзу немiрi.

Егер n=R/4 болса, онда тецдеулер жYЙесi келесi тYрде болады:

ди4 дх

ди ^ дх

^^Ъ

— 24U 1 );

^ = ЩМ (20и — 32и2 — 12uJ dx    v3R2 43        2        1'

диз _ a m (t) /5

dx ^— v3R3 \3 ^U 4

— 32U 3 —~ и

■ (13)

BBtt i v aa ) (

^ид v3R    v 4

— U p ) +

32am(t) c v     (U

— U4);

дt _ A(v ca) , дх    c₂p 3 v 3 ^{1 c.a}

— ^ — Wp^U'—u)

Бастапкы шарты:

и(0) = и t(0) = t i = 1’2,3’4

Уақыт координаты үшін ақырғы-айырмалы әдісті қолдана отырып, аламыз:

ди дт д1

дт

ик+л — и

_D ^к + 0(g)

I к+1 ^— L k g

+ 0(g)

мұнда g – уақыт интервалы.

Орнына қойған соң теңдеулер жүйесі келесі түрде болады:

= - ~ ^(U k,1 - U k-1,1 ) ⁺ ~^ (^24и к,2 - ^24и к,1 ^);

= - ^ (^U k,2 - ^U k-1,' ) ⁺ ~^ (^20и к,3 ^— 32к₂ + ^12и к1 )^;

= - “ ^(и к,4 ^{— и} к-4А ) ⁺   ( R    ^(и к,4 ^{— U} k ) ⁺ -gT ^(и к- ^{— U} k,4 ^);

~^= ^—~^(t k ^— t k-1 ) ⁺ -^ №,4 ^— ^ з ) ^— ~Р~^' ^(и к,4 ^{— и} о ^);  ,

• ^- т        g                    ^с з Р з                        ^с з ^К

Бастапқы шартты қолдана отырып, теңдеулер жүйесін шешу арқылы:

^и к,1 ⁽⁰⁾ = ^и 0.к

^к,1(°) = to,k i=1,2,3,4

кептіру камерасының ұзындығы және уақыт бойынша температура мен ылғал құрамының таралуын аламыз.

Теңдеу жүйесін (14) алгоритм көмегімен ЭЕМ-де іске асыруға болады. 0,1l -ге тең айнымалы х бойынша интеграциялау қадамы үшін кептіру камерасының ұзындығы бойынша ылғал құрамының мынадай анықтамасы алынды:

R и = ~^\UA

2 h,

^2 • 77 (ти + 2T 1 U 1 + 2T ' U '

+ 2г₃и₃ + 2т₄и₄) = - (и 1 + 2и₂ + 3и₃ + 2и₄) 8

Есепті шешуге қажетті берілгендер: a m =0,622*10^-12 м³/с; тыгыздык; р з =750кг/м³; с з = 1,85 кДж/(кг· К); R = 0,0015 м; u p = 0,1 кг/кг, u r =0,33 кг/кг; r = 2400 кДж/кг; А = 0,26 v с.a ; В=0,86*10^-6 t 3 ; v c.a =0,4 м/с; N =2n; ауа ағынының көлденең қимасы s=0,1 м².

Қорытынды

Зерттеу нәтижесінде тамақ өнімдерін кептіру кинетикасын сипаттайтын математи-калық модель жасалды.

Бұл модель жылу және масса алмасу процестерінің өзара байланысын ескеріп, энергия шығынын азайтуға және өнім сапасын сақтауға мүмкіндік береді.

Жұмыстың ғылыми жаңалығы – кептіру процесін сипаттайтын жылу және ылғал теңдеулерін біріктіріп, сандық шешім алу әдісін енгізуінде.

Практикалық маңызы – ұсынылған модельді өндірістік кептіргіш аппараттарды жобалау мен басқару жүйелерінде қолдануға болады.

Болашақ зерттеулер кептіру процесін жасанды интеллект әдістерімен болжау және көпаймақты жылу жүйелерін цифрлық басқару бағытында жалғастырылмақ.

ПАЙДАЛАНҒАН ӘДЕБИЕТ ТІЗІМІ

Kinetics and mathematical modeling of drying of agricultural material. Revista Caatinga, 35(3), 115–126.