Теоретические основы задачного подхода к процессу обучения младших школьников математике

Реализация задачного подхода в процессе обучения в настоящее время является одной из актуальных проблем в сфере образования. С чем это связано? Прежде всего, с теми социальными преобразованиями, которые происходят в условиях современного общества. Они, в свою очередь, оказывают влияние и на развитие педагогических процессов в образовательной системе. Среди них: 1) гуманизация образования, которая выражается в переоценке роли ученика и новом подходе к нему в учебном процессе как субъекту этого процесса; 2) модернизация образования, т.е. построение новой модели системы образования, ориентированной на вхождение в мировое образовательное пространство; 3) процессы интеграции и информатизации образования; 4) разработка и внедрение инновационных педагогических технологий.

Все эти процессы сопровождаются сменой образовательной знаниевой парадигмы, переходом от традиционной модели к построению новой модели образовательной системы. Эта смена парадигмы образования была инициирована созданием теории развивающего обучения, которая и определила характер взаимодействия внешних и внутренних факторов этого процесса. Внешними факторами являются: содержание учебного материала, деятельность учителя, дидактические средства, при помощи которых решаются различные задачи. Внутренними факторами – эмпирический опыт ребенка, готовность к восприятию учебной информации, умственная деятельность, направленная на решение различных задач. В результате такого взаимодействия у учащихся в структуре их умственной деятельности появляются новые качества – новообразования,

обобщенные умения, являющиеся показателями их интеллектуального развития. Учет названных факторов имеет принципиальное значение для теории обучения и обязывает рассматривать во взаимосвязи деятельность учителя и деятельность учащихся не с точки зрения целевого подхода (где цель есть лишь предвосхищаемый результат деятельности), а задачного – при котором создаются объективные условия для достижения этой цели. Таким образом, обучение можно рассматривать как процесс решения различного рода за-дач1. Рассмотрение задачи в структурном контексте как единство цели и условия (или цели в заданных условиях)2, позволит расставить акценты при ответе на вопрос о соотношении целевого и задачного подходов в обучении.

Для полного отражения специфики традиционной модели образования остановимся на описании компонентов процесса с точки зрения их взаимосвязи в целевой модели образования. Известно, что одним из важных компонентов, определяющих стратегическую направленность любой дидактической системы являются ее цели. Анализ педагогических средств вне контекста тех целей на достижение которых они ориентированы, является методологически некорректным, ибо «средства без целей слепы». Однако, как ни парадоксально, но в психолого-педагогической теории начального образования проблема целеполагания в своей сущности является еще не достаточно разработанной. Цели традиционного начального образования, по существу, унаследованы от старой школы. Конкретные цели и содержание современного начального обучения фактически не изменились.

Таб. 1. Сопоставительный анализ целевого и задачного подходов

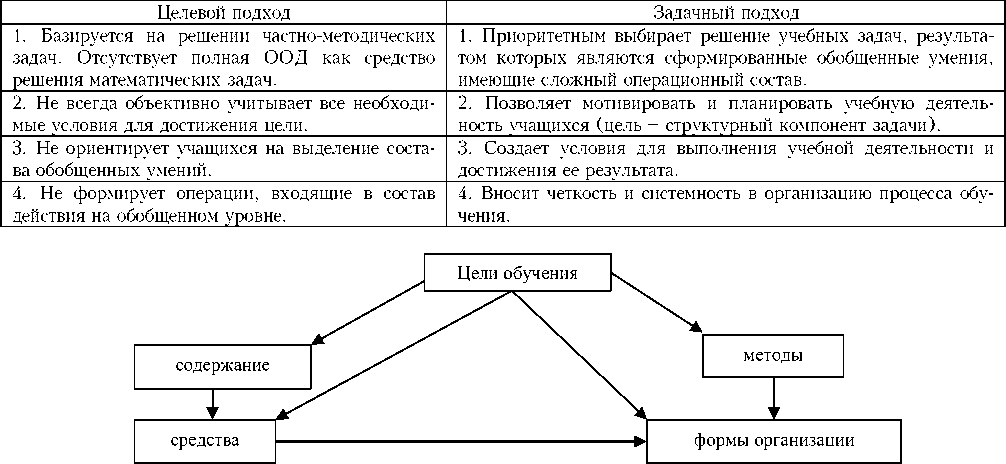
Рис. 1. Традиционная целевая методическая модель системы обучения

Математическая (предметная) задача

МЗ

Решение МЗ – есть математический факт: число, выражение и др. Решить МЗ значит осуществить поиск направленный на выявление определенной последовательности общих математических положений (определений, законов, формул, зависимости, правил, свойств, признаков и т.д.), а так же системы отношений между данными и искомыми

Учебная задача УЗ

Результат решения УЗ есть учебный факт, изменения происходящие в ученике (новообразования), а не в материале с которым он работает.

Учебный факт – знание, те обобщения выполняющие функцию метода обучения или учебного познания

Методическая задача МЕТЗ

Результат решения МЕТЗ – методический факт, например разработка частной методики обучения. Методическая задача решает вопросы касающиеся отбора и структурирования математического содержания, организации процесса решения учебных задач

Рис. 2. Задачная методическая модель системы обучения

Обучение по-прежнему сориентировано на знаниевую парадигму образования, хотя были провозглашены, (но в полной мере не реализованы) задачи, связанные с развитием учащихся. Вклад Л.В.Занкова3, Д.Б.Эльконина4, В.В.Да-выдова5 в решение проблемы развития учащихся привел к определенным сдвигам в понимании сущности начального образования. Однако, эти исследования тормозились руководящими органами народного образования, которые долгое время занимали официальную позицию неприятия направленности обучения на формирование личностных качеств ребенка (новообразований, интеллектуальных умений). Только в связи с гуманизацией образования стала необходимой и возможной разработка целей обучения как исходного компонента методической системы обучения младших школьников, во многом определяющих не только содержание, но и методы, организационные формы и средства обучения. На первый план вместо традиционных целей – усвоения ЗУН выходят цели развития ребенка на основе формирования учебной деятельности. Однако, несмотря на попытку смены приоритетов, подобная формулировка целей, на наш взгляд, имеет некоторые методологические несовершенства. Во-первых, если развитие ребенка предполагается осуществлять на основе формирования учебной деятельности, то последняя выступает уже не как цель, а как средство. Во-вторых, термин «развитие» отражает процессуальную сторону деятельности учителя и дея- тельности учащегося и поэтому не может служить инструментом для описания и характеристики его целей. Цели обучения должны описываться в тех понятиях, которые отражают результат этого процесса, т.е. предполагаемые изменения в структуре когнитивных, личностных и других новообразований учащихся. Новые целевые ориентиры как в теоретическом так и в практическом отношении пока еще слабо разработаны и требуют своей конкретизации. Задач-ный же подход, на наш взгляд, смещает вектор стратегической направленности самого процесса обучения и позволяет исключить названные недостатки в результате иной трактовки методиче- ской системы обучения младших школьников математики. Такой подход предполагает построение системы основополагающих задач для решения проблем связанных с обучением и развитием младших школьников. При системном (задачном) подходе происходит овладение учащимися составом обобщенного способа деятельности, который выполняет функцию метода учения и одновременно создает необходимые условия для его формирования. Т.о., обучение рассматривается как процесс решения целостной системы взаимосвязанных и взаимозависимых задач: математической (предметной), учебной и методической.

Рис. 3. Модель методической системы обучения как системы задач

Рис. 4 . Содержание деятельности учителя

Такой подход к обучению (задачный подход) позволяет изучать и формировать особый вид деятельности, при котором появляется возможность описывать и проектировать деятельность ученика и деятельность учителя как систему процессов решения разных видов задач. Так ученик решает два вида задач – математическую и учебную, а учитель методическую. В процессе обучения происходит взаимодействие двух видов деятельностей учителя и ученика (т.е. взаимодействие внешних и внутренних факторов), которые можно описать через постановку и механизм решения системы трех взаимосвязанных задач. Эта исходная система задач выступает эффективным средством организации процесса обучения. Следовательно, возникает необходимость в модернизации образовательной системы, а значит и в построение новой методической модели системы обучения в рамках задачного подхода6. Построение методической модели как целостной системы задач обладающей свойствами полноты, целостности, структурности и взаимосвязанности является на наш взгляд актуальной проблемой современного школьного образования. Полнота определяется охватом всех видов задач (МЗ, УЗ, МЕТЗ); взаимосвязанность – есть зависимость каждого структурного компонента от его места и функции внутри системы; целостность системы определяется тем, что все компоненты обеспечивают решение единой учебной задачи как системообразующего компонента системы (например, формирование обобщенного способа действия, обобщенного метода учения)7. Механизм функционирования методической модели в учебном процессе как единое целое обеспечивает успешное овладение учащимися математическими понятиями, свойствами, способами действий, выполняющими функцию метода учения. Весь процесс подчинен достижению цели обучения. Цель выступа- ет системообразующим компонентом (Рис.1). Процесс обучения направлен на решение УЗ посредством решения МЗ и МЕТЗ (Рис.2). Относительной данной методической системы задач формируются обобщенные умения, которые являются необходимым и очень важным компонентом как деятельности учащихся так и профессиональной подготовки учителя, особенно в условиях развивающего обучения, которое реализуется в концепции учебной деятельности учащихся. В рамках задачной модели происходит и изменение структуры содержания деятельности учителя (Рис.3). В процессе решения названных задач (МЗ, УЗ, МЕТЗ) формируются обобщенные методические умения относительно этой системы. Овладение соответствующими умениями – важный компонент подготовки учителя (Рис.4).

Таб. 2. Обобщенные методические умения

№ п/п	Содержание умений
	I группа специфико-математические умения	II группа	III группа
		общеинтеллектуальные умения
1.	логико-математический анализ определений понятий, суждений, правил, алгоритмов и т.д.	мотивировать изучение конкретного материала, четко ставить учебную задачу и отбирать соответствующие ей учебные действия и операции	умение реферировать и рецензировать статьи психологопедагогического и методического содержания
2.	логико-математический анализ конкретного содержания определенного раздела учебного материала	на основе поставленных учебных задач выполнять логикодидактический анализ (выделять «ядро-инвариант» и «оболочку» в учебном материале	логико-дидактический анализ содержания учебного материала и реализации в нем определенной математической идеи, линии
3.	поиск способа решения математической задачи, доказательство математического утверждения	организовывать и управлять деятельностью учащихся в процессе решения учебных задач	умение определять иерархию учебных задач конкретной темы, раздела, предмета и конструировать систему ее реализации в условиях обучения
4.	умение работать с учебным материалом и обучать этой работе учащихся	анализировать урок с учетом поставленных учебных задач	создание интегрированной методики обучения в рамках целостной системы взаимосвязанных задач: математических, учебных, методических
5.	умение составлять систему вопросов для проверки усвоения определенного конкретного знания (понятия, отношения, правила)	планировать свою деятельность и прогнозировать ее результаты
6.	умение оценивать и анализировать результаты работы

Таб. 3. Уровни сформированности обобщенных методических умений:

Первый уровень	Второй уровень	Третий уровень
Сводится к осознанию цели выполнения того или иного спецификоматематического и общеинтеллектуального действия, осмыслению его операционного состава, поиску способов выполнения действия на основе образца, предложенного в инструкции	Перенос отдельных сформированных методических умений на новое содержание материала, иногда и на более крупные блоки учебного материала. Перенос этот чаще всего осуществляется на основе осознания цели и путем использования общих рекомендаций	Обобщенные методические умения, которые определяются осознанием не только цели, но и выбором способов деятельности. Этому уровню характерно использование различных средств и методических умений в соответствии с конкретной педагогической ситуацией

В психолого-педагогической литературе существуют различные трактовки понятия «умение»: умение как освоенное действие; умение как способность использовать имеющие знания; умение как совокупность навыков; умение как не вполне завершенный навык или один из существенных этапов в выработке навыка; умение как характеристика овладения действием. Целесообразно в рамках задачного подхода рассматривать умение исходя из структуры учебной деятельности. Учебная деятельность реализуется с помощью определенных учебно-познавательных действий

(например – анализа, моделирования, кодирования, перекодирования, обобщения, конкретизации). В соответствии с назваными обобщенными умениями методическими умениями следует выделить уровни их сформированности. Итак: За-дачный подход в обучении реализуется через целостную систему взаимосвязанных задач которую можно построить на любом содержательном материале как естественно-научных так и гуманитарных дисциплин в системе образования.

THEORETICAL BASES OF THE PROBLEM APPROACH TO MATHEMATICS TRAINING PROCESS OF YOUNGER SCHOOLCHILDREN