Теория APOS в изучении математики (на примере тригонометрии)

2024;28(1):111–124.

Виды человеческой деятельности, а особенно образовательная, связаны с пониманием/взаимопониманием в ходе коммуникации. В связи с этим представляется актуальной разработка средств и методов, позволяющих оценить степень понимания сообщаемой информации обучающемуся.

Педагогами и психологами предпринимаются различные попытки для объяснения ментальных структур, возникающих у студентов в процессе обучения. Такие исследования представляют ценность не только в специальных областях, но и в более широком контексте.

Теория APOS, стоящая на позициях конструктивизма и базирующаяся на работах Ж. Пиаже1, была разработана Э. Дубинским для понимания процесса структурирования абстрактных математических понятий [1]. Она впервые была апробирована на исследовании понятия смежных классов в теории групп [2], затем получила развитие в когнитивном анализе понятия функции [3], линейной алгебре [4] и других разделах математики. Теорию APOS также использовались в теории моделирования и экономике [4], однако в исследовании собственно тригонометрических функций она не применялась. Целью теории APOS является выявление структуризации математической концепции в сознании человека. В соответствии с теорией считается, что в процессе обучения обучающиеся строят ментальные структуры, которые порождаются на базе рефлектирующей абстракции [1]: Действие (Action), Процесс (Process), Объект (Object), Схема (Scheme). Основная идея настоящей работы – применение теории APOS к исследованию формирования ментальных структур обучающихся при изучении математики (на примере тригонометрических функций).

Понятие функции вызывает большие трудности в освоении студентами [5], поскольку включает в себя много других определений. Особую сложность представляют тригонометрические функции, так как тригонометрия интегрирует алгебраические, геометрические и графические рассуждения [6], необходимые при обучении в высшей школе как при изучении самой математики, так и дисциплин естественно-научного цикла (физики, механики, сопромата, электротехники и др.). Интерес к изучению тригонометрических функций с использованием теории APOS вызван, с одной стороны, недостаточным знанием студентами этих функций, с другой – их широким применением в инженерном деле (в расчетах фундаментов, ветровых нагрузок на здания и сооружения, в исследованиях газовых и жидких потоков).

Преподавание тригонометрии в России имеет давние исторические корни2. Большинство работ, посвященных данной теме, направлено на развитие и создание различных методов решения обучающимися типовых тригонометрических уравнений [7], неравенств3 и задач олимпиадного уровня [8; 9]. Имеются работы российских [10] и зарубежных исследователей [6], ориентированные на преподавателей математики, в которых обсуждаются методические проблемы, связанные с анализом тригонометрических функций на единичной окружности и координатной плоскости. Во многих из них основное внимание уделяется внешнему плану восприятия учебного материала обучающимися, в том числе и математических понятий: рассматриваются разные методы решения задач, совершенствуются рабочие программы по математике и др. Однако наряду с проведенными исследованиями в этой области важным остается изучение структур, которые формируются в сознании обучающегося в процессе его изучения математического понятия. Одной из теорий, позволяющей изучать процесс структуризации математического понятия в сознании студента, является теория APOS.

Таким образом, с одной стороны, продолжается интенсивное наращивание, вызванное широкими и разносторонними приложениями тригонометрических функций, исследований методической направленности, с другой – отмечается наличие серьезных и возрастающих проблем с пониманием студентами тригонометрических функций. В рамках нашего исследования продуктивным средством для разрешения данного несоотвествия является использование теории APOS.

Цель исследования состоит в изучении процесса овладения студентами математических понятий (на примере тригонометрических функций) в рамках теории APOS. Гипотеза данного исследования состоит в том, что использование теории APOS позволяет количественно и качественно определить уровень знаний студентов, выявить и оценить характер ошибок, совершаемых студентами в ходе обучения. Для достижения указанной цели необходимо решение следующих задач:

– оценить восприятие студентами тригонометрической функции и анализ ментальных трудностей, возникающих при этом;

– выявить причины ошибок, допускаемых студентами при работе с тригонометрическими функциями.

Обзор литературы

С помощью APOS (Action, Process, Object, Schema) воспроизводятся стадии освоения обучающимся математического понятия.

Теория APOS развивается и используется в основном в трех направлениях:

• 1)    сбор и анализ данных – для тестирования структур, формирующихся в сознании обучающихся после применения или обучения математическому понятию [2];

• 2)    анализ структуры самого математического понятия в ходе обучения [11];

• 3)    разработка эффективных методов обучения, тесно cвязанных с математическими концепциями [12], в частности методика ACE (так называемый цикл ACE (дей-ствие-дискуссии в классе-упражнения)) [2].

Применение теории APOS в обучении математике подробно описывают О. Сефик и соавторы. По их мнению, теория APOS может быть использована для организации учебной деятельности, а также применена для анализа данных, позволяющих выявить ментальные структуры, возникающие в сознании студентов после изучения математических понятий [13].

В настоящей статье на примере тригонометрических функций проводится анализ процесса усвоения математики.

Современные исследования по обучению тригонометрии можно рассматривать с нескольких позиций: ориентированные на изучение сложных с математической точки зрения тем тригонометрии; направленные на совершенствование и создание новых методов и форм эффективного обучения; связанные с изучением интеграции методов и форм обучения с ментальными структурами обучающихся [14].

Тригонометрические функции могут вводиться в практику обучения тремя способами: через соотношения в прямоугольном треугольнике, использование единичной окружности, степенные ряды, т. е. аналитически. Такая множественность влияет на понимание тригонометрических функций. Например, Д. Камбер и Д. Такаси рассматривают проблемы, связанные с пониманием тригонометрических функций как соотношений сторон прямоугольного треугольника [15], а индонезийские ученые [10] – в случае задания на единичном круге.

Во многих зарубежных вузах тригонометрия входит в образовательные программы в качестве раздела математического анализа [16], требующего интеграции фундаментальных понятий математического анализа и свойств тригонометрических функций [16; 17], что позволяет на основе изучения успеваемости студентов по тригонометрии оценивать успехи в усвоении дифференциального исчисления [18].

С эпистемологической позиции о преодолении препятствий в обучении тригонометрии выступают Ч. Л. Макнун с коллегами [6]. Предложено большое число активных и интерактивных методов обучения [19], использования различных частных методик4.

Особый интерес вызывает работа K. Вебера, в которой исследователь, опираясь на идеи Д. Талла [20], предлагает рассматривать тригонометрические функции с трех позиций: процесса, объекта и символа, репрезентирующего процесс или объект, что, по словам автора, позволило студентам лучше понять тригонометрические функции [21]. Здесь же доказана эффективность изучения тригонометрии в рамках практических занятий (в отличие от лекционных).

Предлагаемое исследование, опираясь на теорию APOS, проводится в рамках третьей позиции – изучение ментальных структур студента, возникающих в процессе обучения.

Несмотря на значительное количество публикаций методической направленности, малочисленны публикации, посвященные проблемам понимания студентами математических понятий и концепций. Практически нет работ, в которых проводится анализ ментальных процессов, происходящих в сознании студентов. Авторы впервые в рамках теории APOS исследуют процесс структуризации математических понятий и проводят классификацию ошибок в случае тригонометрических функций.

Материалы и методы

В качестве теоретической основы исследования выбрана теория APOS, которая базируется на представлении о рефлектирующей абстракции5 [1]. Рефлектирующая абстракция делает упор на общие свойства действий, не зависящие от математических объектов, с которым совершаются действия.

Теория APOS фокусируется на построении моделей, объясняющих ментальные процессы обучающегося при попытке понять ту или иную математическую концепцию. И. Арнон и соавторы утверждают, что «APOS – это теория того, как математические понятия могут быть выучены» [12].

Рассмотрим каждый этап овладения понятиями в теории APOS.

• 1.    Действие (Action) – это стадия, на которой каждый шаг процесса обучения

• 2.    Процесс (Process) – стадия, на которой происходит повторение действий и их осмысление; студент переходит от опоры на внешние подсказки к внутреннему контролю. Данная стадия характеризуется способностью представлять себе выполнение шагов без необходимости осуществлять их эксплицитно, пропускать шаги, а также обращать их вспять. Обучающийся может отражать во внутреннем плане сами действия без привязки к конкретным математическим объектам. Реализация этой стадии состоит в интериоризации действий в процедуры, которые учащиеся могут выполнять без посторонней помощи или обобщать действия, выполняемые на конкретных объектах, в процессы, которые действительны для любого объекта того же типа. Процессы помогают студентам абстрагироваться от конкретных реализаций, взять под контроль само действие безотносительно внешнего объекта и тем самым сделать гибким использование действий. Это предполагает умение пользоваться определенным алгоритмом решения со стандартными действиями и формулами. Так, поиск значения функции синуса для заданного угла может быть сведен к определению значения по единичному кругу, где значения синуса распределены

• 3.    Объект (Object) – это стадия, в ходе которой обучающийся осознает процесс как целостность, к которому можно применить новые действия. Данный этап предусматривает умение студента вычленить подклассы в пределах заданного концепта. В этом случае происходит инкапсуляция процесса. Следует заметить, что такое понятие как «объект», возникшее на основе процесса, предполагает возврат к стадии процесса в случае необходимости⁷, т. е. объект де-инкапсулирован. Такая возможность двигаться в разных направлениях составляет существенный аспект математической деятельности⁸. Для тригонометрических функций это свидетельствует о том, что студент может определить, например, интервалы возрастания и убывания функций.

• 4.    Схема (Schema) - это стадия, включающая упорядоченное множество связей в сознании студента между различными действиями, процессами и объектами, которые предполагается использовать при решении данной конкретной проблемы или построении новых знаний.

четко представляется студентом и направляется внешними инструкциями. «Действие – это трансформация какого-либо объекта, воспринимаемая индивидом как принципиально внешняя и как требующая выполнения пошаговой инструкции (заданной эксплицитно или же воспроизводимой по памяти) о том, как производить соответствующие операции»6. Действия основаны на правилах и алгоритмах, отрабатываемых многократно, но связанных с конкретными объектами. Для случая тригонометрических функций это предполагает, что студент должен знать понятие функции, уметь отличать тригонометрические функции от других видов, вычислять значение тригонометрической функции в определенной точке.

на вертикальной оси. Перечисленные операции на этой стадии студент выполняет без посторонней помощи.

В качестве основных использовались следующие методы:

• -    системный подход - анализ научно-педагогических публикаций по проблематике исследования - выявление и обобщение теоретических основ проблемы исследования;

• -    контент-анализ результатов, полученных с помощью опроса, - анализ взаимосвязей между этапами теории APOS; направлен на изучение процесса понимания студентами тригонометрических функций;

• -    статистическая обработка с группировкой данных - исследование в ходе из у ч ения студентами тригонометрических функций ментальных структур в их сознании, выявление закономерностей и извлечение выводов.

Данная работа включает в себя сбор и анализ результатов опроса с последующими их разбором и классификацией ошибок студентов на стадиях теории APOS, а также рекомендации по их исправлению.

В качестве базы эмпирического этапа исследования выбран Казанский государственный архитектурно-строительный университет. В опросе приняли участие студенты четырех групп первого курса направления подготовки «Строительство»: 1 группа – 26 чел., 2 – 26, 3 и 4 – по 25 чел. Для анализа мы не делаем различий между группами, принимаем их как единую выборку численностью 102 участника. Все участники на момент проведения исследования были проинформированы о цели исследования и выразили готовность к участию в нем.

Исследование проводилось по следующим этапам:

• 1.    Теоретический - уточнение концептуальных вопросов исследования, научное обоснование и разработка основных разделов опросника, с помощью которого возможно, согласно теории APOS, определить насколько студенты готовы к пониманию математических объектов, а равно и оценить стадии его понимания. Применяемые методы: системный анализ литературы по данной тематике, статистический метод обработки данных.

• 2.    Экспериментальный – опрос, в ходе которого респондентами выполнялись задания опросника, созданного на предыдущем этапе исследования. При обработке тестов выявлялись ошибки, определялся их характер и стадия APOS, на которой находится студент (согласно его понимания математического понятия). Ниже приведен перечень вопросов.

• 1.    Напишите своими словами, что такое функция.

• 2.    Опишите своими словами функцию sin x.

• 3.    Напишите, чему равно: sin ⁴ , sin ⁴, sin30 ^o , sin180 ^o ?

• 4.    Отметьте на единичном круге решение уравнений: sin x = 0,5, sin x = 1, sin x = 1,5.

• 5.    Существуют ли x е R , решения неравенства sin x ≥ ? Если нет, объясните почему.

• 6.    Для каких значений х функция синус убывает, почему?

• 7.    Постройте график функции у = а • sin x . Как изменится график функции при различных значениях параметра а ?

• 8.    На графике функции у = а • sin x изобразите график функции у = а • sin3 x .

• 9.    Напишите в порядке возрастания числа: sin 115°, sin250°, sin370°.

• 10.    Чему равно число sin π ? Ответ поясните.

• 11.    Чему равно sin² x + cos² x и почему?

• 12.    Что больше sin 23° или sin 37°? Ответ поясните.

• 13.    Что означает периодичность функции sin x и какой у нее период? Какой период функции sin 2 x ?

• 14.    Верна ли формула sin( x + y ) = = sin x + sin y ? Если нет, напишите правильную формулу.

• 3.    Обработка, систематизация и интерпретация полученных данных: статистические методы, группировка, контент-анализ.

Использование в вопроснике только одной функции у = sin x (за исключением 11-го вопроса) обусловлено тем, что оно позволяет осуществить сквозной анализ усвоения этой функции как типичной тригонометрической функции; в случае других тригонометрических функций теория APOS применяется аналогично.

Результаты исследования

Приведенные выше вопросы соответствуют стадиям теории APOS. Задания 1 и 2 опросника относятся к так называемой стадии Pre-action [16]. Они позволяют обнаружить студентов, не готовых к восприятию понятия тригонометрической функции в силу отсутствия у них основополагающих знаний.

Как показал анализ ответов на эти вопросы, на стадии Pre-action находится 10 студентов, не справившихся с заданиями. Заметим, что на подготовительных курсах вуза вопросы 1 и 2 задавались и школьникам, ответы которых примерно совпадают с ответами студентов-первокурсников (не справились с заданием 5 чел. из 43). Вопросы 3, 9, 10, 12 отражают стадию действия; 4, 6, 14 – процесса; 5, 11, 13 – объекта; 7, 8 – схемы. По каждой стадии теории APOS составим таблицы.

Как видно из таблицы 1, основная часть студентов эту стадию успешно преодолевает; в среднем 85,3 % обучающихся полностью справились с заданиями. Однако ответы на 10-й вопрос показали, что некоторые из них справляются с вычислением соответствующих значений, но пояснить не могут. Эта стадия преодолевается с помощью преподавателя, и студенты формально выполняют такие задания. В ответах пользуются тригонометрическим кругом. На этой стадии студенты в основном производят только заранее известные алгоритмические действия, но при этом совершают ошибки, например, забывая писать скобки.

3^

Т ак, в выражении sin — - 2 л надо писать

• f 3л       )                               .71

sin     - 2 л и далее, а в строке sin--

I 2     )                           2

надо писать sin ^- ^ J .Пренебрежение скобками – одна из наиболее частых ошибок.

Т а б л и ц а 1. Итоговые показатели по этапу «Действие» в теории APOS

T a b l e 1. Final figures for the Action in APOS theory stage

Номер вопроса / Question number	Полный корректный ответ / Full correct answer	Неполный, частично правильный ответ / Incomplete, partially correct answer	Ошибочный ответ / Wrong answer	Нет ответа / No answer
3	100	1	0	1
9	79	1	20	2
10	67	28	2	5
12	102	0	0	0
Средние значения, % / Average values, %	85,3	7,4	5,4	1,9

Источник : здесь и далее в статье все таблицы составлены авторами. Source : Hereinafter in the article all tables are compiled by the authors.

В одной из работ указано, что поскольку sin2 п - периодическая функция,

. (3к )   . Кк )

то sin      = sin     но это неверно.

( 2 )     ( 2 )

Полученные результаты по стадии «Процесс» продемонстрированы в таблице 2. Студенты могут представить решение (в основном на единичном круге), достаточно легко ориентируются в показе значений функций, однако затрудняются в учете периодичности функции. Наименьшее число правильных ответов было дано на 6-й вопрос: они путали интервалы убывания с интервалами, где функция имеет отрицательные значения. Большинство обучающихся использовали на этой стадии единичный круг, что затруднило нахождение интервалов монотонности. В среднем по данной стадии полный ответ дали 63,8 % студентов.

Как видно из таблицы 3, задания стадии «Объект» решили в среднем 29,4 % студентов. Остальные студенты плохо представляют себе свойства функций, особенно возрастание, убывание и периодичность. Например, определяя период функции sin2x, ими допускались следующие ошибки: одни писали, что у sin2x период вдвое больше, чем у sinx, другие – вообще не указали периоды. Так, неполный частичный правильный ответ на 13-й вопрос соответствует тому, что студенты дали только определение периодичности либо указали периоды функций синуса.

17 из 102 студентов полностью владеют теоретическим и практическим материалами по свойствам тригонометрических функций и их графиков; 66 чел. не могут представить преобразование графика синуса тройного аргумента [1]. Таким образом, в среднем только 22,5 % студентов способны к реализации этапа «Схема», согласно теории APOS (табл. 4).

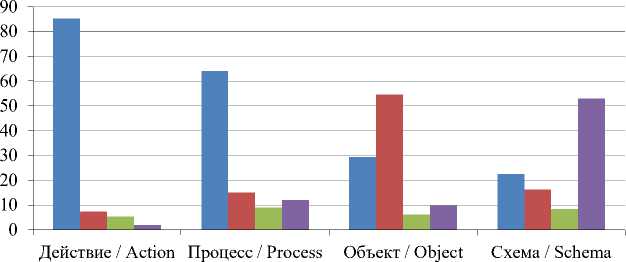
Динамику распределения правильных, ошибочных, неполных и работ без ответа по соответствующим стадиям проиллюстрируем на следующей диаграмме (рисунок), полученной на основании сводной таблицы 5.

Рисунок демонстрирует тот факт, что переход от стадии к стадии средний процент полностью решенных заданий снижается, а процент ошибок в среднем увеличивается (небольшое исключение на стадии «Схема», но это корректируется ростом нерешенных задач).

Т а б л и ц а 2. Итоговые показатели по этапу «Процесс» в теории APOS

T a b l e 2. Final figures for the Process stage in APOS theory

Номер вопроса / Question number	Полный корректный ответ / Full correct answer	Неполный, частично правильный ответ / Incomplete, partially correct answer	Ошибочный ответ / Wrong answer	Нет ответа / No answer
4	86	9	7	0
6	43	23	16	20
14	66	14	5	17
Средние значения, % / Average values, %	63,8	15,0	9,1	12,1

Т а б л и ц а 3. Итоговые показатели по этапу «Объект» в теории APOS

T a b l e 3. Final Figures for the Object Stage in APOS Theory

Номер вопроса / Question number	Полный корректный ответ / Full correct answer	Неполный, частично правильный ответ / Incomplete, partially correct answer	Ошибочный ответ / Wrong answer	Нет ответа / No answer
5	37	51	7	7
11	17	82	0	3
13	36	34	12	20
Средние значения, % / Average values, %	29,4	54,6	6,2	9,8

Т а б л и ц а 4. Итоговые показатели по этапу «Схема» в теории APOS

T a b l e 4. Total figures for the Scheme stage in the APOS theory

Номер вопроса / Question number	Полный корректный ответ / Full correct answer	Неполный, частично правильный ответ / Incomplete, partially correct answer	Ошибочный ответ / Wrong answer	Нет ответа / No answer
7	29	23	8	42
8	17	10	9	66
Средние значения, % / Average values, %	22,5	16,2	8,3	53,0

Т а б л и ц а 5. Сводная таблица средних значений результатов по каждому этапу, %

T a b l e 5. Summary table of average results for each stage, %

Этапы / Stages	Действие / Action	Процесс / Process	Объект / Object	Схема / Schema	Средние значения / Average values
Решенные задания / Solved tasks	85,3	64,0	29,4	22,5	51,000
Неполностью выполнено / Incomplete	7,3	15,0	54,6	16,2	23,275
Решено с ошибками / Solved with errors	5,4	9,0	6,2	8,3	7,225
Не решено / Unsolved	2,0	12,0	9,8	53,0	19,200

■ Ряд 1 / Row 1  ■ Ряд 2 / Row 2  ■ Ряд 3 / Row 3  ■ Ряд 4 / Row 4

Р и с у н о к. Распределение средних результатов по каждой стадии APOS

F i g u r e. Distribution of average results for each APOS stage

Примечания : ряд 1 – полностью решенные задания; ряд 2 – решено частично; ряд 3 – решенные с ошибками; ряд 4 – нерешенные.

Notes : Row 1 – completely solved tasks; row 2 – partially solved; row 3 – solved with errors; row 4 – unsolved.

Источник : составлено авторами.

Source : Compiled by the authors.

Наибольшее число частично решенных заданий, судя по среднему проценту, наблюдается на стадии «Объект». В основном это связано с демонстрацией функции синуса на тригонометрическом круге, по которой не видны промежутки убывания или возрастания функции. Вместе с тем студенты, владеющие знанием графического представления синуса в виде синусоиды, хорошо справляются с заданиями данной стадии.

Допускаемые ошибки на основе APOS анализа можно классифицировать как концептуальные и процессуальные [13]. К концептуальным относятся следующие ошибки: непонимание понятия функции, желание работать только с взаимно-однозначными функциями и тождествами, неумение распознавать свойства сложных тригонометрических функций на основе знаний свойств основных элементарных тригонометрических функций, перенесение свойств линейной функции на тригонометрические (например, sin(x + y) = sinx + + siny); к процессуальным – неумение делать упрощения в формулах, ошибки в знаках и др. В комментариях к таблице 2 приведены примеры процессуальных ошибок.

На основании результатов, представленных в таблицах 3 и 4, можно утверждать, что около 70 % опрошенных совершают концептуальные ошибки. На стадиях «Действие» и «Процесс» совершаются в основном процессуальные ошибки, поскольку обучение осуществляется по инструкции.

Обсуждение и заключение

Поэтапное исследование познавательного процесса, на что ориентирована теория APOS, позволяет выяснить причины тех или иных действий учащихся, степень понимания, хотя на проблему понимания в математике есть различные точки зрения9. Объединение общих взглядов на природу математических концептов и когнитивной теории APOS позволяет осознать связь между математической деятельностью и математическим мышлением10. Теория APOS способствуют выявлению потенциала обучающегося, а также конкретизации формы помощи студенту. Разработка методических материалов по математике вызывает определенные трудности, а понимание процесса структуризации понятия в сознании студента помогает выстраивать эффективную методическую работу [22; 23]. В процессе обучения преподаватели и обучающиеся часто испытывают затруднения в коммуникации [24], связанные с проблемами понимания преподавателями механизмов структуризации понятия в сознании обучающегося. Теория APOS дает продуктивную возможность преодоления таких препятствий.

Анализ ответов студентов показал, что большинство из них (99 % с учетом неполных ответов) в ходе изучения тригонометрических функций находятся на стадии «Действие», что демонстрирует слабость самостоятельного и критического мышления у современных студентов. По результатам экспериментов выявлено, что причиной ошибок являются непонимание студентами сути определения функции, формальное понимание свойств тригонометрических функций, отсутствие связи между математическим символом и его визуальным представлением (подтверждает результаты, полученные в работе [25]). В школьной программе много внимания уделяется тригонометрии на единичной окружности, что наносит некоторый ущерб пониманию тригонометрических функций как соответствий и их графическому представлению. Слабый уровень знаний студентов этого раздела математики приводит к необходимости дополнительных занятий по тригонометрии для студентов первого курса, так как тригонометрические функции используются в математическом анализе, уравнениях математической физики и других разделах дисциплин, входящих в обязательную часть обучения. Полученные теоретические и экспериментальные результаты позволяют сделать следующие выводы.

• 1.    Изучение усвоения тригонометрических функций с использованием теории APOS подтвердило эффективность его применения, позволило выявить трудности, возникающие перед обучающимися, и детализировать понимание студентами этих функций. Выводы, касающиеся снижения числа студентов, владеющих математикой, при движении от стадии к стадии подтверждают результаты других работ [16].

• 2.    Ошибки студентов носят концептуальный и процессуальный характер. Как правило, концептуальные ошибки

• 3.    Практическая значимость исследования заключается в том, что в работе показано, как APOS позволяет количественно и качественно определить уровень компетентности каждого студента в данной области математики. Последнее дает возможность сделать обучение более

совершаются на стадиях «Объект» и «Схема», процессуальные – на стадиях «Действие» и «Процесс». Используемая теория позволяет выделить ошибки в наглядном виде и дает возможность провести соответствующие методические мероприятия, направленные на устранение препятствий с учетом индивидуальности обучающегося.

релевантным как для преподавателей, так и для студентов и в комплексе с другими методами может успешно применяться для улучшения образовательного процесса в целом.

Материалы статьи могут быть интересны учителям математики и преподавателям вузов с целью детального изучения когнитивной деятельности обучающихся и классификации ошибок с последующими рекомендациями методического характера. Выбор других разделов математики как предметов использования теории APOS предполагается в дальнейших исследованиях авторов.