Теплообмен при охлаждении молочной сыворотки в потоке

Техническая реализация одного из способов кристаллизации лактозы в молочной сыворотке основана на использовании в качестве охладителя-кристаллизатора пластинчатого скребкового теплообменника. Кристаллизация лактозы развивается в сложных гидродинамических условиях и в широком температурном диапазоне и т.п. [1, 5, 6].

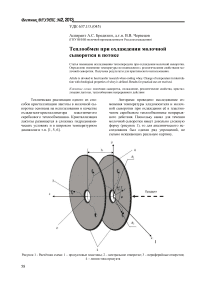
Авторами проведено исследование изменения температуры хладоносителя и молочной сыворотки при охлаждении её в пластинчатом скребковом теплообменнике непрерывного действия. Поскольку канал для течения молочной сыворотки имеет довольно сложную форму (рисунок 1), то для аналитического исследования был сделан ряд упрощений, не сильно искажающих реальную картину.

Рисунок 1 - Расчётная схема: 1 – продуктовые пластины; 2 – центральное отверстие; 3 – периферийные отверстия;

4 – линии тока продукта

Распределение температуры продукта в охлаждающем элементе будем изучать с помощью дифференциальных уравнений тепло- переноса в движущихся жидких средах, записанных в цилиндрической системе координат при осесимметричном распределении темпера туры, без учета диссипации энергии:

д T    д T    ( д ² T  1 д T  д ² T )

v_r    + v z    = a . ++ 2

д r       д z    (д r ²    r д r    д z ² ,

где T - температура в точках продукта, оС ; r и z - цилиндрические координаты точки продук та; vr и vz - проекции скорости точек продукта на оси r и z; a - коэффициент температуропроводности.

Полагаем, что осевая скорость продукта vz значительно меньше радиальной vr и окружной vф скоростей, поэтому в уравнении

(1) положим v — * 0. Для определения ради-z дz альной скорости vr воспользуемся дифферен циальным уравнением стационарного осесимметричного стационарного течения сплошной среды в напряжениях [2] в проекции на радиальное направление r, полагая в нем реологические константы и плотность продукта р не зависящими от температуры для данной пары продуктовых пластин.

Реологические исследования молочной сыворотки позволяют с большой точностью принять в качестве ее реологической модели степенную модель Оствальда-Де Виля [3]. Для такой модели компоненты тензора напряжений, входящие в уравнение (1), при сделанных ранее предположениях имеют вид [4]:

Trr =- Р + 2 к H-1    , д r

Г „ =- Р + 2 к\Н r , ,     (2)

*„ = kM V оz где к и n - реологические константы молочной сыворотки: H - интенсивность скоростей деформации, равная:

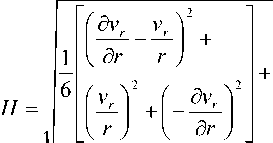
1 ( дv_r ) ² + -I — I

4 ( д z )

Величина к|НГ 1 может рассматриваться как некоторая кажущаяся (эффективная) вязкость:

° ^- r , r

+ — дr      дz   r

F + ¹      ^rz ^T - ^Т фф

F r +^11

р I д r     д z       r

где T rr, T фф - нормальные напряжения на площадках перпендикулярных соответственно радиальной r и окружной ф осям, т rz - касательное напряжение на площадках, перпендикулярных осям r и z.

Уравнение неразрывности (несжимаемости), справедливое для любой жидкой среды при сделанных предположениях, имеет вид:

^ rv ) = 0 , д r

Интегрируя уравнение (5), находим:

v r = ^{1 f} ( z ) .

r

Температуру в продукте определяем

по

. д T _ уравнению (1) с учетом v — * 0 . Для этого z дz подставим в левую часть данного уравнения выражение радиальной скорости (6) и разделим его левую и правую части на коэффициент температуропроводности a. После этого получим:

f ( z ) 1 д т    д ² т 1 д т д ² т

--= —т +--+ — т , (7) r а д r    д r ²    r д r    д z ²

Поскольку точного аналитического решения данного уравнения получить нельзя, воспользуемся приближенным решением, заключающемся в частичном осреднении его конвективной части (левая часть уравнения) по толщине зазора между дисками и использовании метода последовательных приближений. Для этого в левой части равенства (7) положим h f (z) * f(z) = 2 /f (z) dz • Функция f(z), учиты-h J^X вающая разность давления и вязкостные свойства молочной сыворотки, получена ав- торами ранее при исследовании гидродина- мики пластинчатого скребкового менника. Она имеет вид:

теплооб-

f ( z ) =-

⁽ Р 1 ^- Р 2 ^{)( 1} - n ) 1 n k ( R 2 - n - Ri n )

n n +1

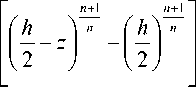
Проинтегрировав функцию f ( z ) (8) в пределах от 0 до ^h , находим:

f ^{( z} ) =

2 n

2 n + 1

h ) ⁿ Г ⁽ P i ^- P 2 ^{)( 1 - n} ) 1 n

2 ) [ k ( R 2 - ⁿ - R 1ⁿ )

. (9)

Таким образом, уравнение (7) заменится приближенным уравнением, приведенным к стандартной форме:

d T + 1 d T ( i — в ) +d T = o , (io)

o r   r о r         оz где через B обозначена величина f (z) из (9)

деленная на a , т. е.:

в = fz ) ,         (11)

a

Данное уравнение решаем при следую- щих граничных условиях:

r = R 1 , T = T z = 0,

T = T ₃ , ,                   ⁽¹²⁾

z = h ,

T = T, где T3 и T4 - температуры продукта на стен- ках дисков.

Решение линейного уравнения (10) найдем методом разделения переменных, добавив к его общему решению частное решение специального вида. Для этого положим:

T ( r , z ) = R ( r ) ■ Z ( z )

+ T ₃ + z ( T , - T ₃ ) h

Подстановкой этого выражения T в (10) и разделением переменных, получим для функций R(r) и Z(z) обыкновенные диффе- ренциальные уравнения:

Z " + Z ² Z = 0 ,           (14)

rR ‘ + R ‘ ( 1 - B ) - Z rR = 0 ,    (15)

где Z ² - константа разделения.

Решение уравнения (14) имеет вид:

Z ( z ) = C 1 cos Z z + C ₂ sin Z z , (16) В силу двух последних граничных условий (12) и выражения (13) функция Z ( z ) должна обращаться в ноль при z = 0 и z = h . Отсюда следует:

C = 0, Z = k^ , k = 1,2,... да , (17) 1 h

То есть общее решение уравнения (10) будет представлено рядом Фурье по синусам.

Уравнение (15) является уравнением Бесселя произвольного порядка, зависящего от константы B . Поскольку такие функции не табулированы, то дальше будем решать уравнение (10) методом последовательных приближений. Для этого проведем оценку порядка слагаемых в этом уравнении, приведя его к безразмерному виду. Напишем соотношения между размерными и безразмерными величинами:

T = T ₀ T , r = R ₂ r , z = hz ,     (18)

где T0 - характерная размерная величина ис- комой функции, T - безразмерная искомая функция, r - безразмерная радиальная координата, R2 - характерный радиальный размер, z - безразмерная осевая координата. В качестве характерной осевой координаты взято расстояние h между дисками.

Перейдя в уравнении (10) к безразмер- ным величинам получим:

h ² d ² T ( 1 - B ) h²

R[ d r ²" ⁺ R 2

1 dT d2 T n x--+ —=00

r d r d z ²

Таким образом, в безразмерном уравнении (19) порядки слагаемых будут определяться только порядками коэффициентов в этих слагаемых. Для оценки порядка этих коэффи- циентов примем следующие порядки конструктивных параметров охладителя и параметров обрабатываемого продукта: h~0,01м, R1 ~0,01м, R2 ~0,1м, q ~10 4 м3/c, a ~10 6 м2/c, k ~10Па ■ с,.

n ~1

Коэффициент B во втором слагаемом согласно (9) и (11) будет иметь порядок 10⁴, т. е. В >>1 . Коэффициент в последнем слагаемом уравнения (19) имеет порядок 1. Принимая во h ² Bh ²

внимание, что — <<---- ~ 1 , оставим в

R ₂ ²      R ₂ ²

уравнении (19), а значит и в уравнении (10), два последних слагаемых. На этом основании уравнение (10) для нулевого приближения при условии В >>1 примет вид:

Используя формулу для определения коэффициентов ряда Фурье на интервале 0 <  z <  h , найдем:

C j

jп

T - T 3 -

⁽ T 1 ^- T 4 ^{) c}oS J K

j ^п R г

2 Bh ^{2 1}

—

B дT д T „

--+-- г = 0 r д r д z

Решим уравнение (20) методом разделения переменных, представив его решение в виде (13). После разделения переменных для функций R ( r ) и Z ( z ) получим обыкновенные дифференциальные уравнения:

R'

Л ² --r,

RB

И (14), решением которого будет функция (16) при значениях констант (17). Решение уравнения первого порядка с разделяющимися переменными (21) запишется в виде:

- r ²

R ( r ) = C з e ² B ,

где С 3 - постоянная интегрирования. Таким образом, на основании (13), (16), (17) и (22) получим решение уравнения (20) в виде ряда:

j 2 Я1 2

,     .      ”        -----7 r        ITT

T ( r , z ) = Z C₍e ²     sin^— z +

, = 1 '                         h

^{+ T} 3 ⁺ V ^{( T} 4 - ^T 3 ) h

где С к = С 2 С ₃ и индекс j показывает, что эта

константа буд ет зависеть от номера j собственных чисел λ из (17).

Найдем постоянные интегрирования С , используя первое граничное условие (12), т. е. T ( R 1 , z ) = T 1 . На основании этого условия и соотношения (23) получим уравнение для определения С_j :

T 1 - T 3 - z- ( T 4 - T 3 ) = h

to

=Z С j=1

j ² п ²

--Г ^R 1

e 2 Bh

k

• j п sin z

h

Таким образом, распределение температуры в пространстве между продуктовыми пластинами в нулевом приближении на основании (23) и (25) примет следующий вид:

^{T ( r} , ^z ) =

2 Z   T - T3 - п j=1 j L(Ti -T4)cos j п.

( R 2 - r 2 ) _e 2 Bh ^{2   1}

■ j^п . sin--- z + h

^{+ T} 3 + T ^{( T} 4 - ^T 3 )

h

Для нахождения первого приближения решения уравнения (10) подставим найденное решение нулевого приближения в ранее отброшенное слагаемое д ² T этого уравнения.

д r¹

После этого придем к неоднородному линей-

ному уравнению в частных производных:

B д T д¹ Т

----1--7 = r дr д z2

j [ T - T 3 - ( T 1 - T 4) cos j п ]

^{2 п} V^-1 /       ., .,     \ j ² п ²

= 77"Z f    ^{j п}    _г) T Bh ²⁽ R ^{1- r} ) . ^{j п z} ■

B ^h j =1 1 1-- — r I e             sin----

' I      Bh^г J                       h

Будем искать решение этого уравнения в таком же виде, как и решение уравнения (20) нулевого приближения, т. е.:

to

T ( r , z ) = Z F j ( r ) sin^ Л z + T ₃ - _( T ₃ - T 4 ) ,     ⁽²⁸⁾

~=T          h          h где F (r) - неизвестная пока функция, зависящая от координаты r и номера j собственных чисел λ из (17). Подстановкой выражения T(r, z) из (28) в левую часть уравнения (27) и

приравниванием коэффициентов при sin jп z в h левой и правой частях уравнения (27), получим обыкновенное линейное уравнение первого порядка относительно функции F(r):

BdF_k j 2 п 2

+ F = r dr     h 2

= - 2 0 j [ T , - T 3 - ( T 1 - T 4 ) cos j п ] х

Bh

х 1

-

k

j п

Bh ²

>

r

^(R 2 - ^{r 2 )} e

J

Решением этого уравнения является функция:

Fk( r ) =

—

П [ T — T 3 — ( T — T , ) cos J * ] x Bh

X

2   22

^r j ⁿ

—

( 2 4 Bh'

I

r

V ( R 1 — r ²) e ^{2 Bh}       +

, (30)

j ⁿ 2

2 ^r

+ C_k*e ^{2 Bh}

где C *

-

постоянная интегрирования.

Ha основaнии (28) и (30) имеем:

T ^{( r} , z ) =

П

—

B ² h ²

to j=11

f j [ T 1 — T 3 — ( T 1 — T 4 ) cos j n ]

r ²

—

^ П r ⁴ I e 2 Bh ² I

¹—_r ( R 2— r ² ) +

2 Bh ^{2   1}

+ C >

j 2     _r

2 Bh ²

zL ,2

CX

^{j п}

X sin--- z + T h ³

— z ( T 3 — T 4 ) .

h

Постоянную интегрирования C ' нахо-

дим так же, как и постоянную С _j для нулевого приближения, т. е. из условия T ( R 1 , z ) = T 1 . Точно так же, как и в равенстве (24), получим разложение функции, стоящей в левой части этого равенства в ряд Фурье по синусам. Из формулы для определения коэффициентов

этого ряда находим:

C ; =— j

T 1

—

T 3 —( T 1 — T 4 Г

cos j n

X

X

( 2 B ² h h

I j ^п

+ R 1²

—

• 2 _2 A ^{j п} в ²

T- ^_R 4 I e 2 ^{Bh 2}

2 Bh ^{2 1} I

Подставив данное выражение С * в правую часть равенства (31), приведем его к виду: ^{T (} r , z ) =

to

=—П nr B2 h2 2 .

f j [ T — T 3 — ( T 1 — T 4 ) cos j n ]

x e

r2

—

^R 1 ²

—

^ П - ( r ⁴ — R k) —

2 Bh ^{2        1}

2B2 h2

J n

X

j 24 ( R 2 2 Bh ²

— r ²)

jn sin z h

C+ T 3

— z ( T 3 — T 4 ) .

h

Таким образом, формула (33) применена для расчета температуры продукта как при центральном способе его подачи, так и при периферийном способе подачи в пространство между дисками. Полученные формулы позволяют проводить расчёт процесса охлаждения

при поточной кристаллизации лактозы в молочной сыворотке в потоке и определять основные параметры пластинчатых скребковых теплообменных аппаратов.